Hostname: page-component-cb9f654ff-c75p9 Total loading time: 0 Render date: 2025-08-12T19:39:27.477Z Has data issue: false hasContentIssue false
  • English
  • Français

EXPONENTIAL SUMS OVER PRIMES IN SHORT INTERVALS AND AN APPLICATION TO THE WARING–GOLDBACH PROBLEM

Part of: Exponential sums and character sums Additive number theory; partitions

Published online by Cambridge University Press:  17 February 2016

Bingrong Huang
Bingrong Huang*
Affiliation:
School of Mathematics, Shandong University, Jinan, Shandong 250100, China email brhuang@mail.sdu.edu.cn
Get access

Abstract

Let 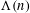${\rm\Lambda}(n)$ be the von Mangoldt function, $x$ be real and 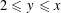$2\leqslant y\leqslant x$ . This paper improves the estimate for the exponential sum over primes in short intervals

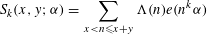$$\begin{eqnarray}S_{k}(x,y;{\it\alpha})=\mathop{\sum }_{x<n\leqslant x+y}{\rm\Lambda}(n)e(n^{k}{\it\alpha})\end{eqnarray}$$
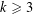when $k\geqslant 3$ for ${\it\alpha}$ in the minor arcs. When combined with the Hardy–Littlewood circle method, this enables us to investigate the Waring–Goldbach problem concerning the representation of a positive integer $n$ as the sum of $s$ 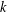  $k$ th powers of almost equal prime numbers, and improve the results of Wei and Wooley [On sums of powers of almost equal primes. Proc. Lond. Math. Soc. (3) 111(5) (2015), 1130–1162].

MSC classification

Primary: 11L20: Sums over primes
Secondary: 11P32: Goldbach-type theorems; other additive questions involving primes

Information

Type
Research Article
Information
Mathematika , Volume 62 , Issue 2 , 2016 , pp. 508 - 523
Copyright
Copyright © University College London 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Daemen, D., The asymptotic formula for localized solutions in Waring’s problem and approximations to Weyl sums. Bull. Lond. Math. Soc. 42(1) 2010, 75–82; MR 2586968 (2011b:11139).Google Scholar
Huang, B. R., Strong orthogonality between the Möbius function and nonlinear exponential functions in short intervals. Int. Math. Res. Not. IMRN 2015(23) 2015, 12713–12736, doi:10.1093/imrn/rnv091.Google Scholar
Huang, B. R. and Wang, Z. W., Exponential sums over primes in short intervals. J. Number Theory 148 2015, 204–219.CrossRefGoogle Scholar
Huxley, M. N., On the difference between consecutive primes. Invent. Math. 15 1972, 164–170; MR 0292774 (45 #1856).Google Scholar
Kawada, K. and Wooley, T. D., On the Waring–Goldbach problem for fourth and fifth powers. Proc. Lond. Math. Soc. (3) 83(1) 2001, 1–50.Google Scholar
Kumchev, A. V., On Weyl sums over primes and almost primes. Michigan Math. J. 54(2) 2006, 243–268.CrossRefGoogle Scholar
Kumchev, A. V., On Weyl sums over primes in short intervals. In Number Theory—Arithmetic in Shangri-La (Series on Number Theory and its Applications 8 ), World Scientific Publishing (Hackensack, NJ, 2013), 116–131.Google Scholar
Liu, J. Y., Lü, G. S. and Zhan, T., Exponential sums over primes in short intervals. Sci. China Ser. A 49(5) 2006, 611–619.CrossRefGoogle Scholar
Liu, J. Y. and Zhan, T., Estimation of exponential sums over primes in short intervals II. In Analytic Number Theory: Proceedings of a Conference in Honor of Heini Halberstam, Birkhäuser (1996), 571–606.Google Scholar
Liu, J. Y. and Zhan, T., Estimation of exponential sums over primes in short intervals I. Monatsh. Math. 127(1) 1999, 27–41.Google Scholar
Lü, G. S. and Lao, H. X., On exponential sums over primes in short intervals. Monatsh. Math. 151(2) 2007, 153–164.CrossRefGoogle Scholar
Vaughan, R. C., Recent work in additive prime number theory. In Proceedings of the International Congress of Mathematicians (Helsinki, 1978), Acad. Sci. Fennica (Helsinki, 1980), 389–394; MR 562631 (81j:10077).Google Scholar
Vinogradov, I. M., Estimation of certain trigonometric sums with prime variables. Izv. Acad. Nauk SSSR 3 1939, 371–398.Google Scholar
Wei, B. and Wooley, T. D., On sums of powers of almost equal primes. Proc. Lond. Math. Soc. (3) 111(5) 2015, 1130–1162, doi:10.1112/plms/pdv048.Google Scholar
Zhan, T., On the representation of large odd integer as a sum of three almost equal primes. Acta Math. Sin. 7(3) 1991, 259–272.Google Scholar