Article contents
DOUBLE-NORMAL PAIRS IN SPACE
Published online by Cambridge University Press: 14 August 2014
Abstract
A double-normal pair of a finite set 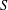 $S$ of points that spans
$S$ of points that spans 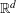 $\mathbb{R}^{d}$ is a pair of points
$\mathbb{R}^{d}$ is a pair of points 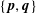 $\{\mathbf{p},\mathbf{q}\}$ from
$\{\mathbf{p},\mathbf{q}\}$ from 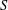 $S$ such that
$S$ such that 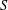 $S$ lies in the closed strip bounded by the hyperplanes through
$S$ lies in the closed strip bounded by the hyperplanes through 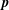 $\mathbf{p}$ and
$\mathbf{p}$ and 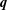 $\mathbf{q}$ perpendicular to
$\mathbf{q}$ perpendicular to 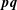 $\mathbf{p}\mathbf{q}$. A double-normal pair
$\mathbf{p}\mathbf{q}$. A double-normal pair 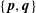 $\{\mathbf{p},\mathbf{q}\}$ is strict if
$\{\mathbf{p},\mathbf{q}\}$ is strict if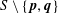 $S\setminus \{\mathbf{p},\mathbf{q}\}$ lies in the open strip. The problem of estimating the maximum number
$S\setminus \{\mathbf{p},\mathbf{q}\}$ lies in the open strip. The problem of estimating the maximum number 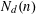 $N_{d}(n)$ of double-normal pairs in a set of
$N_{d}(n)$ of double-normal pairs in a set of  $n$ points in
$n$ points in 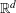 $\mathbb{R}^{d}$, was initiated by Martini and Soltan [Discrete Math. 290 (2005), 221–228]. It was shown in a companion paper that in the plane, this maximum is
$\mathbb{R}^{d}$, was initiated by Martini and Soltan [Discrete Math. 290 (2005), 221–228]. It was shown in a companion paper that in the plane, this maximum is 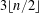 $3\lfloor n/2\rfloor$, for every
$3\lfloor n/2\rfloor$, for every 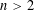 $n>2$. For
$n>2$. For 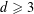 $d\geqslant 3$, it follows from the Erdős–Stone theorem in extremal graph theory that
$d\geqslant 3$, it follows from the Erdős–Stone theorem in extremal graph theory that 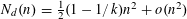 $N_{d}(n)=\frac{1}{2}(1-1/k)n^{2}+o(n^{2})$ for a suitable positive integer
$N_{d}(n)=\frac{1}{2}(1-1/k)n^{2}+o(n^{2})$ for a suitable positive integer 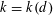 $k=k(d)$. Here we prove that
$k=k(d)$. Here we prove that 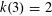 $k(3)=2$ and, in general,
$k(3)=2$ and, in general, 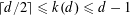 $\lceil d/2\rceil \leqslant k(d)\leqslant d-1$. Moreover, asymptotically we have
$\lceil d/2\rceil \leqslant k(d)\leqslant d-1$. Moreover, asymptotically we have 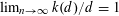 $\lim _{n\rightarrow \infty }k(d)/d=1$. The same bounds hold for the maximum number of strict double-normal pairs.
$\lim _{n\rightarrow \infty }k(d)/d=1$. The same bounds hold for the maximum number of strict double-normal pairs.
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 2014
References
- 2
- Cited by

