No CrossRef data available.
Article contents
THE DENSITY OF NUMBERS REPRESENTED BY DIAGONAL FORMS OF LARGE DEGREE
Published online by Cambridge University Press: 23 April 2018
Abstract
Let 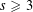 $s\geqslant 3$ be a fixed positive integer and let
$s\geqslant 3$ be a fixed positive integer and let 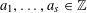 $a_{1},\ldots ,a_{s}\in \mathbb{Z}$ be arbitrary. We show that, on average over
$a_{1},\ldots ,a_{s}\in \mathbb{Z}$ be arbitrary. We show that, on average over  $k$ , the density of numbers represented by the degree
$k$ , the density of numbers represented by the degree 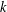 $k$ diagonal form decays rapidly with respect to
$k$ diagonal form decays rapidly with respect to 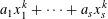 $$\begin{eqnarray}a_{1}x_{1}^{k}+\cdots +a_{s}x_{s}^{k}\end{eqnarray}$$
$$\begin{eqnarray}a_{1}x_{1}^{k}+\cdots +a_{s}x_{s}^{k}\end{eqnarray}$$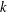 $k$ .
$k$ .
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 2018
References
Bennett, M. A., Dummigan, N. P. and Wooley, T. D., The representation of integers by binary additive forms. Compos. Math.
111(1) 1998, 15–33.Google Scholar
Bukh, B., Lower bounds on the easier Waring problem. MathOverflow. URL:https://mathoverflow.net/questions/64649/lower-bounds-on-the-easier-waring-problem.Google Scholar
Iwaniec, H. and Kowalski, E., Analytic Number Theory
(Colloquium Publications 53
), American Mathematical Society (Providence, RI, 2004).Google Scholar
Landau, E., Ueber die zahlentheoretische Funktion 𝜑(x) und ihre Beziehung zum Goldbachschen satz. Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen
1900
1900, 177–186.Google Scholar
Mahler, K., Zur Approximation algebraischer Zahlen III. Acta Math.
62(1) 1933, 91–166. Über die mittlere Anzahl der Darstellungen grosser Zahlen durch binäre Formen.Google Scholar
Nathanson, M., Additive number theory. In The Classical Bases
(Graduate Texts in Mathematics 164
), Springer (1996).Google Scholar
Soundararajan, K., Small gaps between prime numbers: the work of Goldston-Pintz-Yıldırım. Bull. Amer. Math. Soc.
44
2007, 1–18.CrossRefGoogle Scholar
Stewart, C. L. and Xiao, S. Y., On the representation of integers by binary forms. Preprint, 2016,arXiv:1605.03427.Google Scholar
Vaughan, R. and Wooley, T., Waring’s problem: a survey. In Number Theory for the Millennium, III (Urbana, IL, 2000) (2002), 301340.Google Scholar
Wooley, T., Quasi-diagonal behaviour in certain mean value theorems of additive number theory. J. Amer. Math. Soc.
7
1994, 221–245.Google Scholar

