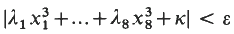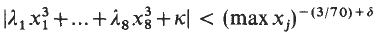Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Brüdern, Jörg
1988.
Cubic Diophantine inequalities.
Mathematika,
Vol. 35,
Issue. 1,
p.
51.
Baker, R. C.
Brüdern, J.
and
Wooley, T. D.
1995.
Cubic Diophantine inequalities.
Mathematika,
Vol. 42,
Issue. 2,
p.
264.
Li, Hong Ze
2001.
Cubic Diophantine Inequalities.
Acta Mathematica Sinica, English Series,
Vol. 17,
Issue. 1,
p.
153.
Xue, Boqing
2014.
Diophantine inequality involving binary forms.
Frontiers of Mathematics in China,
Vol. 9,
Issue. 3,
p.
641.