No CrossRef data available.
Article contents
CONTRACTIVE FAMILIES ON COMPACT SPACES
Published online by Cambridge University Press: 14 May 2014
Abstract
A family 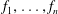 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}f_1,\ldots,f_n$ of operators on a complete metric space
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}f_1,\ldots,f_n$ of operators on a complete metric space 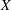 $X$ is called contractive if there exists
$X$ is called contractive if there exists 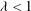 $\lambda < 1$ such that for any
$\lambda < 1$ such that for any 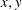 $x,y$ in
$x,y$ in 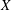 $X$ we have
$X$ we have 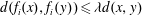 $d(f_i(x),f_i(y)) \leq \lambda d(x,y)$ for some
$d(f_i(x),f_i(y)) \leq \lambda d(x,y)$ for some 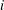 $i$. Stein conjectured that for any contractive family there is some composition of the operators
$i$. Stein conjectured that for any contractive family there is some composition of the operators 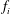 $f_i$ that has a fixed point. Austin gave a counterexample to this, and asked whether Stein’s conjecture is true if we restrict to compact spaces. Our aim in this paper is to show that, even for compact spaces, Stein’s conjecture is false.
$f_i$ that has a fixed point. Austin gave a counterexample to this, and asked whether Stein’s conjecture is true if we restrict to compact spaces. Our aim in this paper is to show that, even for compact spaces, Stein’s conjecture is false.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 2014

