Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Brown, Ronald
Hardy, Lew
and
Morris, Sidney A.
1975.
The homotopy groups of ann-fold wedge.
Mathematische Zeitschrift,
Vol. 143,
Issue. 2,
p.
119.

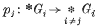 may be defined by requiring it to be trivial on
may be defined by requiring it to be trivial on 