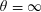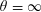Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Pratt, Kyle
and
Robles, Nicolas
2018.
Perturbed moments and a longer mollifier for critical zeros of
$$\zeta $$
ζ
.
Research in Number Theory,
Vol. 4,
Issue. 1,
Wu, Xiaosheng
2019.
The twisted mean square and critical zeros of Dirichlet L-functions.
Mathematische Zeitschrift,
Vol. 293,
Issue. 1-2,
p.
825.
Pratt, Kyle
Robles, Nicolas
Zaharescu, Alexandru
and
Zeindler, Dirk
2020.
More than five-twelfths of the zeros of $$\zeta $$ are on the critical line.
Research in the Mathematical Sciences,
Vol. 7,
Issue. 1,
K, Papageorgiou
and
G, Papageorgiou
2023.
An innovative method and a medical screening device for cancer detection in real-time.
Annals of Mathematics and Physics,
Vol. 6,
Issue. 1,
p.
075.
Das, Mithun Kumar
and
Pujahari, Sudhir
2024.
Mean of the product of derivatives of Hardy's Z-function with Dirichlet polynomial.
Journal of Number Theory,
Vol. 258,
Issue. ,
p.
334.