No CrossRef data available.
Article contents
The symmetric elements of a semi-simple S-ring
Published online by Cambridge University Press: 26 February 2010
Extract
Let Γ be a finite group of order n and let K be a field whose characteristic does does not divide n. The group ring K(Γ) is then an involution algebra if we define 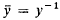 for y є Γ and extend by linearity, so that ¯ is trivial on K. A subalgebra T of K(Γ) is said to be an S-ring on Γ (see [4]) if there exists a decomposition
for y є Γ and extend by linearity, so that ¯ is trivial on K. A subalgebra T of K(Γ) is said to be an S-ring on Γ (see [4]) if there exists a decomposition
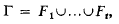
of Γ into non-empty, pairwise disjoint subsets Fi with the properties that the elements 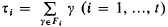 of K(Γ) form a K-basis of T and that for each τi there exists a τj such that
of K(Γ) form a K-basis of T and that for each τi there exists a τj such that 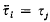 .
.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 1970
References
2.Frame, J. S., “The double cosets of a finite group”, Bull. Amer. Math. Soc., 47 (1941), 458–467.CrossRefGoogle Scholar
3.McEvett, A. W., “Forms over semi-simple algebras with involution”, J. Algebra, 12 (1969), 105–113.CrossRefGoogle Scholar
4.Tamaschke, Olaf, “A generalized character theory on finite groups”, Proceedings of international conference on theory of groups, Canberra 1965 (Gordon and Breach, New York, 1967).Google Scholar
5.Wielandt, Helmut, “Zur theorie der einfach transitiven Permutationsgruppen”, Mat. Zeit., 52 (1949), 384–393.CrossRefGoogle Scholar

