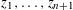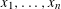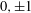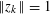Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Hájek, Petr
Kania, Tomasz
and
Russo, Tommaso
2020.
Separated sets and Auerbach systems in Banach spaces.
Transactions of the American Mathematical Society,
Vol. 373,
Issue. 10,
p.
6961.