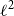1. Introduction
Weighted finite automata (WFAs) are an expressive class of models representing functions defined over sequences. The approximate minimization problem is concerned with finding an automaton that approximates the behavior of a given minimal WFA, while being smaller in size. Clearly, the two automata compute different languages, so the objective is to minimize the approximation error (Balle et al., Reference Balle, Panangaden and Precup2015, Reference Balle, Panangaden and Precup2019). Approximate minimization can be particularly useful in the context of spectral learning algorithms (Bailly et al., Reference Bailly, Denis and Ralaivola2009; Hsu et al., Reference Hsu, Kakade and Zhang2012; Balle et al., Reference Balle, Carreras, Luque and Quattoni2014a; Hsu et al., Reference Hsu, Kakade and Zhang2012). When applied to a learning task, such algorithms can be viewed as working in two steps. First, they compute a minimal WFA that explains the training data exactly. Then, they obtain a model that generalizes to the unseen data by producing a smaller approximation to the minimal WFA, thus preventing overfitting of the data.
A key point in solving approximation tasks is to choose how to quantify the error. We propose to rewrite the problem in terms of Hankel matrices, mathematical objects strictly related to WFAs, and to measure the error in terms of the spectral norm. This allows us to exploit the work of Adamyan, Arov, and Krein which has come to be known as AAK theory (Adamyan et al., Reference Adamyan, Arov and Krein1971): a series of results connecting the theory of complex functions to Hankel matrices. The core of this theory provides us with theoretical guarantees for the exact computation of the spectral norm of the error and a method to construct the optimal approximation. We show that the spectral norm of the Hankel matrix of a WFA can be computed accurately in polynomial time (cubic in the number of states of the automaton). This is a great advantage compared, for example, to behavioral norms, which are easier to interpret but harder to compute (Balle et al., Reference Balle, Gourdeau, Panangaden, Chatzigiannakis, Indyk, Kuhn and Muscholl2017, Reference Balle, Gourdeau and Panangaden2022). The spectral norm has another advantage over WFA-specific behavioral metrics. In fact, an important extension of this work is the application of the method to other classes of models. In the one-letter case, a similar algorithm can be found to approximate a black-box model over sequential data using a WFA (Lacroce et al., Reference Lacroce, Panangaden, Rabusseau, Chandlee, Eyraud, Heinz, Jardine and van Zaanen2021). With this in mind, we think that it is preferable to consider a norm defined on the input-output function – or the Hankel matrix – rather than the parameters of the specific model considered.
We summarize our main contributions:
-
• We apply AAK theory to the approximate minimization problem of WFAs by establishing a correspondence between the parameters of a WFA and the coefficients of a complex function on the unit circle. To the best of our knowledge, this paper represents the first attempt to apply AAK theory to WFAs.
-
• We present a theoretical analysis of the optimal spectral-norm approximate minimization problem of WFAs, based on their connection with finite-rank infinite Hankel matrices. We provide a closed-form solution for real weighted automata
 $A=\langle \boldsymbol{\alpha }, \mathbf{A}, \boldsymbol{\beta } \rangle$
over a one-letter alphabet, under the assumption
$A=\langle \boldsymbol{\alpha }, \mathbf{A}, \boldsymbol{\beta } \rangle$
over a one-letter alphabet, under the assumption
 $\rho (\mathbf{A})\lt 1$
on the spectral radius. We bound the approximation error, both in terms of the Hankel matrix (spectral norm) and of the rational function computed by the WFA (
$\rho (\mathbf{A})\lt 1$
on the spectral radius. We bound the approximation error, both in terms of the Hankel matrix (spectral norm) and of the rational function computed by the WFA (
 $\ell ^2$
norm).
$\ell ^2$
norm). -
• We propose a self-contained algorithm that returns the unique optimal spectral-norm approximation of a given size in polynomial time.
-
• We tighten the connection, made in (Balle et al. (Reference Balle, Panangaden and Precup2019), between WFAs and discrete dynamical systems, by adapting some of the control theory concepts to this setting, for example the all-pass system (Glover, Reference Glover1984).
In this paper, we present and expand the results of our previous work (Balle et al., Reference Balle, Lacroce, Panangaden, Precup, Rabusseau, Bansal, Merelli and Worrell2021). The contents of this paper are organized as follows. In Section 2, we define the notation that will be used throughout the paper and review a series of well-known results from the theory of automata and from functional analysis. In Section 3, we establish the framework to reformulate the approximate minimization problem in terms of Hankel operators and AAK theory. Section 4 presents the theoretical foundation of our contribution and a closed-form solution for our problem. Section 5 shows how to implement the algorithm derived from the solution obtained in the previous section, while in Section 6 we provide an example and compute the optimal approximation of a given WFA. Section 7 discusses the related work in approximate minimization and control theory. Finally, in Sections 8 and 9 we highlight possible directions for future work, analyze the limitations of this approach, and summarize our contribution.
2. Background
In this section, we recall the fundamental definitions and preliminary results that are used throughout the paper. After defining weighted finite automata and Hankel matrices, we will provide an overview of AAK theory. We will see in the next section that our objective is to rewrite the approximate minimization problems as low-rank approximation of a Hankel matrix. In the paper, We use AAK theory to solve the low-rank approximation problem while preserving the Hankel property.
2.1 Preliminaries
We denote with
![]() $\mathbb{N}$
,
$\mathbb{N}$
,
![]() $\mathbb{Z}$
,
$\mathbb{Z}$
,
![]() $\mathbb{R}$
, and
$\mathbb{R}$
, and
![]() $\mathbb{C}$
the set of natural, integers, real and complex numbers, respectively. We use bold letters for vectors and matrices; all vectors considered are column vectors. We denote with
$\mathbb{C}$
the set of natural, integers, real and complex numbers, respectively. We use bold letters for vectors and matrices; all vectors considered are column vectors. We denote with
![]() $\mathbf{1}$
the identity matrix, specifying its dimension only when not clear from the context. We refer to the
$\mathbf{1}$
the identity matrix, specifying its dimension only when not clear from the context. We refer to the
![]() $i$
-th row and the
$i$
-th row and the
![]() $j$
-th column of
$j$
-th column of
![]() $\mathbf{M}$
by
$\mathbf{M}$
by
![]() $\mathbf{M}(i,:)$
and
$\mathbf{M}(i,:)$
and
![]() $\mathbf{M}({:},j)$
. Given a matrix
$\mathbf{M}({:},j)$
. Given a matrix
![]() $\mathbf{M}\in \mathbb{R}^{p\times q}$
of rank
$\mathbf{M}\in \mathbb{R}^{p\times q}$
of rank
![]() $n$
, a rank factorization is a factorization
$n$
, a rank factorization is a factorization
![]() $\mathbf{M}=\mathbf{P}\mathbf{Q}$
, where
$\mathbf{M}=\mathbf{P}\mathbf{Q}$
, where
![]() $\mathbf{P} \in \mathbb{R}^{p\times n}$
,
$\mathbf{P} \in \mathbb{R}^{p\times n}$
,
![]() $\mathbf{Q} \in \mathbb{R}^{n\times q}$
, and
$\mathbf{Q} \in \mathbb{R}^{n\times q}$
, and
![]() $\textrm{rank}(\mathbf{M})=\textrm{rank}(\mathbf{P})=\textrm{rank}(\mathbf{Q})=n$
. Let
$\textrm{rank}(\mathbf{M})=\textrm{rank}(\mathbf{P})=\textrm{rank}(\mathbf{Q})=n$
. Let
![]() $\mathbf{M} \in \mathbb{R}^{p \times q}$
of rank
$\mathbf{M} \in \mathbb{R}^{p \times q}$
of rank
![]() $n$
, the compact singular value decomposition SVD of
$n$
, the compact singular value decomposition SVD of
![]() $\mathbf{M}$
is the factorization
$\mathbf{M}$
is the factorization
![]() $\mathbf{M}=\mathbf{U}\mathbf{D}\mathbf{V}^{\top }$
, where
$\mathbf{M}=\mathbf{U}\mathbf{D}\mathbf{V}^{\top }$
, where
![]() $\mathbf{U}\in \mathbb{R}^{p\times n}$
,
$\mathbf{U}\in \mathbb{R}^{p\times n}$
,
![]() $\mathbf{D}\in \mathbb{R}^{n\times n}$
,
$\mathbf{D}\in \mathbb{R}^{n\times n}$
,
![]() $\mathbf{V}\in \mathbb{R}^{q \times n}$
are such that
$\mathbf{V}\in \mathbb{R}^{q \times n}$
are such that
![]() $\mathbf{U}^{\top }\mathbf{U}=\mathbf{V}^{\top }\mathbf{V}=\mathbf{1}$
, and
$\mathbf{U}^{\top }\mathbf{U}=\mathbf{V}^{\top }\mathbf{V}=\mathbf{1}$
, and
![]() $\mathbf{D}$
is a diagonal matrix. The columns of
$\mathbf{D}$
is a diagonal matrix. The columns of
![]() $\mathbf{U}$
and
$\mathbf{U}$
and
![]() $\mathbf{V}$
are called left and right singular vectors, while the entries of
$\mathbf{V}$
are called left and right singular vectors, while the entries of
![]() $\mathbf{D}$
are the singular values. The Moore-Penrose pseudo-inverse
$\mathbf{D}$
are the singular values. The Moore-Penrose pseudo-inverse
![]() $\mathbf{M}^+$
of
$\mathbf{M}^+$
of
![]() $\mathbf{M}$
is the unique matrix such that
$\mathbf{M}$
is the unique matrix such that
![]() $\mathbf{M}\mathbf{M}^+\mathbf{M}=\mathbf{M}$
,
$\mathbf{M}\mathbf{M}^+\mathbf{M}=\mathbf{M}$
,
![]() $\mathbf{M}^+\mathbf{M}\mathbf{M}^+=\mathbf{M}^+$
, with
$\mathbf{M}^+\mathbf{M}\mathbf{M}^+=\mathbf{M}^+$
, with
![]() $\mathbf{M}^+\mathbf{M}$
and
$\mathbf{M}^+\mathbf{M}$
and
![]() $\mathbf{M}\mathbf{M}^+$
Hermitian (Zhu, Reference Zhu1990). The spectral radius
$\mathbf{M}\mathbf{M}^+$
Hermitian (Zhu, Reference Zhu1990). The spectral radius
![]() $\rho (\mathbf{M})$
of a matrix
$\rho (\mathbf{M})$
of a matrix
![]() $\mathbf{M}$
is the largest modulus among its eigenvalues.
$\mathbf{M}$
is the largest modulus among its eigenvalues.
A Hilbert space is a complete normed vector space where the norm arises from an inner product. A linear operator
![]() $T: X \rightarrow Y$
between Hilbert spaces is bounded if it has finite operator norm, that is
$T: X \rightarrow Y$
between Hilbert spaces is bounded if it has finite operator norm, that is
![]() $\|T\|_{op} = \sup _{\|g\|_X\leq 1}\|Tg\|_Y \lt \infty$
. We denote by
$\|T\|_{op} = \sup _{\|g\|_X\leq 1}\|Tg\|_Y \lt \infty$
. We denote by
![]() $\mathbf{T}$
the (infinite) matrix associated with
$\mathbf{T}$
the (infinite) matrix associated with
![]() $T$
by some (canonical) orthonormal basis on
$T$
by some (canonical) orthonormal basis on
![]() $H$
. An operator is compact if the image of the unit ball in
$H$
. An operator is compact if the image of the unit ball in
![]() $X$
is relatively compact. Given Hilbert spaces
$X$
is relatively compact. Given Hilbert spaces
![]() $X, Y$
and a compact operator
$X, Y$
and a compact operator
![]() $T:X \rightarrow Y$
, we denote its adjoint by
$T:X \rightarrow Y$
, we denote its adjoint by
![]() $T^*$
. The singular numbers
$T^*$
. The singular numbers
![]() $\{\sigma _n\}_{n \geq 0}$
of
$\{\sigma _n\}_{n \geq 0}$
of
![]() $T$
are the square roots of the eigenvalues of the self-adjoint operator
$T$
are the square roots of the eigenvalues of the self-adjoint operator
![]() $T^* T$
, arranged in decreasing order. A
$T^* T$
, arranged in decreasing order. A
![]() $\sigma$
-Schmidt pair
$\sigma$
-Schmidt pair
![]() $\{\boldsymbol{\xi }, \boldsymbol{\eta }\}$
for
$\{\boldsymbol{\xi }, \boldsymbol{\eta }\}$
for
![]() $T$
is a couple of norm
$T$
is a couple of norm
![]() $1$
vectors such that:
$1$
vectors such that:
![]() $\mathbf{T}\boldsymbol{\xi }=\sigma \boldsymbol{\eta }$
and
$\mathbf{T}\boldsymbol{\xi }=\sigma \boldsymbol{\eta }$
and
![]() $\mathbf{T}^*\boldsymbol{\eta }= \sigma \boldsymbol{\xi }$
. The Hilbert-Schmidt decomposition provides a generalization of the compact SVD for the infinite matrix of a compact operator
$\mathbf{T}^*\boldsymbol{\eta }= \sigma \boldsymbol{\xi }$
. The Hilbert-Schmidt decomposition provides a generalization of the compact SVD for the infinite matrix of a compact operator
![]() $T$
using singular numbers and orthonormal Schmidt pairs:
$T$
using singular numbers and orthonormal Schmidt pairs:
![]() $\mathbf{T}\mathbf{x}=\sum _{n\geq 0}\sigma _n\langle \mathbf{x},\boldsymbol{\xi }_n \rangle \boldsymbol{\eta }_k$
(Zhu, Reference Zhu1990). The spectral norm
$\mathbf{T}\mathbf{x}=\sum _{n\geq 0}\sigma _n\langle \mathbf{x},\boldsymbol{\xi }_n \rangle \boldsymbol{\eta }_k$
(Zhu, Reference Zhu1990). The spectral norm
![]() $\|\mathbf{T}\|$
of the matrix representing the operator
$\|\mathbf{T}\|$
of the matrix representing the operator
![]() $T$
is the largest singular number of
$T$
is the largest singular number of
![]() $T$
. Note that the spectral norm of
$T$
. Note that the spectral norm of
![]() $\mathbf{T}$
corresponds to the operator norm of
$\mathbf{T}$
corresponds to the operator norm of
![]() $T$
.
$T$
.
Let
![]() $\ell ^2$
be the Hilbert space of square-summable sequences over
$\ell ^2$
be the Hilbert space of square-summable sequences over
![]() $\Sigma ^*$
, with norm
$\Sigma ^*$
, with norm
![]() $\|f\|_2^2=\sum _{x\in \Sigma ^*}|f(x)|^2$
and inner product
$\|f\|_2^2=\sum _{x\in \Sigma ^*}|f(x)|^2$
and inner product
![]() $\langle f, g \rangle = \sum _{x \in \Sigma ^*}f(x)g(x)$
for
$\langle f, g \rangle = \sum _{x \in \Sigma ^*}f(x)g(x)$
for
![]() $f,g \in \mathbb{R}^{\Sigma ^*}$
. Let
$f,g \in \mathbb{R}^{\Sigma ^*}$
. Let
![]() $\mathbb{T}=\{z\in \mathbb{C}: |z|=1\}$
be the complex unit circle,
$\mathbb{T}=\{z\in \mathbb{C}: |z|=1\}$
be the complex unit circle,
![]() $\mathbb{D}=\{z\in \mathbb{C}: |z|\lt 1\}$
the (open) complex unit disc. Let
$\mathbb{D}=\{z\in \mathbb{C}: |z|\lt 1\}$
the (open) complex unit disc. Let
![]() $1\lt p\lt \infty$
,
$1\lt p\lt \infty$
,
![]() $\mathscr{L}^{\,p}(\mathbb{T})$
be the space of measurable functions on
$\mathscr{L}^{\,p}(\mathbb{T})$
be the space of measurable functions on
![]() $\mathbb{T}$
for which the
$\mathbb{T}$
for which the
![]() $p$
-th power of the absolute value is Lebesgue integrable. For
$p$
-th power of the absolute value is Lebesgue integrable. For
![]() $p=\infty$
, we denote with
$p=\infty$
, we denote with
![]() $\mathscr{L}^{\,\infty }(\mathbb{T})$
the space of measurable functions that are bounded, with norm
$\mathscr{L}^{\,\infty }(\mathbb{T})$
the space of measurable functions that are bounded, with norm
![]() $\|f\|_{\infty }=\sup \{|f(x)|: x\in \mathbb{T}\}$
.
$\|f\|_{\infty }=\sup \{|f(x)|: x\in \mathbb{T}\}$
.
2.2 Hankel matrix and weighted automata
Let
![]() $\Sigma$
be a fixed finite alphabet and
$\Sigma$
be a fixed finite alphabet and
![]() $\Sigma ^*$
be the set of all finite strings with symbols in
$\Sigma ^*$
be the set of all finite strings with symbols in
![]() $\Sigma$
. We denote with
$\Sigma$
. We denote with
![]() $\varepsilon$
the empty string. Given
$\varepsilon$
the empty string. Given
![]() $p,s \in \Sigma ^*$
, we denote with
$p,s \in \Sigma ^*$
, we denote with
![]() $ps$
the string obtained by their concatenation. Let
$ps$
the string obtained by their concatenation. Let
![]() $f : \Sigma ^* \to \mathbb{R}$
be a function defined on sequences, we consider the bi-infinite matrix
$f : \Sigma ^* \to \mathbb{R}$
be a function defined on sequences, we consider the bi-infinite matrix
![]() $\mathbf{H}_f \in \mathbb{R}^{\Sigma ^* \times \Sigma ^*}$
having rows and columns indexed by strings and defined by
$\mathbf{H}_f \in \mathbb{R}^{\Sigma ^* \times \Sigma ^*}$
having rows and columns indexed by strings and defined by
![]() $\mathbf{H}_f(p,s) = f(ps)$
for
$\mathbf{H}_f(p,s) = f(ps)$
for
![]() $p, s \in \Sigma ^*$
.
$p, s \in \Sigma ^*$
.
Definition 1.
A matrix
![]() $\mathbf{H} \in \mathbb{R}^{\Sigma ^* \times \Sigma ^*}$
is
Hankel
if for all
$\mathbf{H} \in \mathbb{R}^{\Sigma ^* \times \Sigma ^*}$
is
Hankel
if for all
![]() $p, p^{\prime}, s, s^{\prime} \in \Sigma ^*$
such that
$p, p^{\prime}, s, s^{\prime} \in \Sigma ^*$
such that
![]() $p s = p^{\prime} s^{\prime}$
, we have
$p s = p^{\prime} s^{\prime}$
, we have
![]() $\mathbf{H}(p,s) = \mathbf{H}(p^{\prime},s^{\prime})$
.
$\mathbf{H}(p,s) = \mathbf{H}(p^{\prime},s^{\prime})$
.
Given a Hankel matrix
![]() $\mathbf{H} \in \mathbb{R}^{\Sigma ^* \times \Sigma ^*}$
, there is a unique function
$\mathbf{H} \in \mathbb{R}^{\Sigma ^* \times \Sigma ^*}$
, there is a unique function
![]() $f : \Sigma ^* \to \mathbb{R}$
such that
$f : \Sigma ^* \to \mathbb{R}$
such that
![]() $\mathbf{H}_f = \mathbf{H}$
. Intuitively, the Hankel property tells us that each entry of the matrix only depends on the composition of the coordinates. Since rows and columns are indexed using strings, then the value stored in each entry only depends on the string obtained by concatenating the coordinates.
$\mathbf{H}_f = \mathbf{H}$
. Intuitively, the Hankel property tells us that each entry of the matrix only depends on the composition of the coordinates. Since rows and columns are indexed using strings, then the value stored in each entry only depends on the string obtained by concatenating the coordinates.
Weighted finite automata are a class of models defined over sequential data. A weighted finite automaton (WFA) of
![]() $n$
states over
$n$
states over
![]() $\Sigma$
is a tuple
$\Sigma$
is a tuple
![]() $A = \langle \boldsymbol{\alpha }, \{ A_a\}_{a \in \Sigma }, \boldsymbol{\beta } \rangle$
, where
$A = \langle \boldsymbol{\alpha }, \{ A_a\}_{a \in \Sigma }, \boldsymbol{\beta } \rangle$
, where
![]() $\boldsymbol{\alpha },$
$\boldsymbol{\alpha },$
![]() $\boldsymbol{\beta } \in \mathbb{R}^n$
are the vector of initial and final weights, respectively, and
$\boldsymbol{\beta } \in \mathbb{R}^n$
are the vector of initial and final weights, respectively, and
![]() $\mathbf{A}_a \in \mathbb{R}^{n \times n}$
is the matrix containing the transition weights associated with each symbol
$\mathbf{A}_a \in \mathbb{R}^{n \times n}$
is the matrix containing the transition weights associated with each symbol
![]() $a\in \Sigma$
. Every WFA
$a\in \Sigma$
. Every WFA
![]() $A$
with real weights realizes (or computes) a function
$A$
with real weights realizes (or computes) a function
![]() $f_A : \Sigma ^* \to \mathbb{R}$
, that is given a string
$f_A : \Sigma ^* \to \mathbb{R}$
, that is given a string
![]() $x = x_1 \cdots x_t \in \Sigma ^*$
, it returns
$x = x_1 \cdots x_t \in \Sigma ^*$
, it returns
![]() $f_A(x) = \boldsymbol{\alpha } ^\top \mathbf{A}_{x_1} \cdots \mathbf{A}_{x_t} \boldsymbol{\beta } = \boldsymbol{\alpha } ^\top \mathbf{A}_x \boldsymbol{\beta }$
. A function
$f_A(x) = \boldsymbol{\alpha } ^\top \mathbf{A}_{x_1} \cdots \mathbf{A}_{x_t} \boldsymbol{\beta } = \boldsymbol{\alpha } ^\top \mathbf{A}_x \boldsymbol{\beta }$
. A function
![]() $f : \Sigma ^* \to \mathbb{R}$
is called rational if there exists a WFA
$f : \Sigma ^* \to \mathbb{R}$
is called rational if there exists a WFA
![]() $A$
that realizes it. Given
$A$
that realizes it. Given
![]() $f : \Sigma ^* \to \mathbb{R}$
, we can use the Hankel matrix
$f : \Sigma ^* \to \mathbb{R}$
, we can use the Hankel matrix
![]() $\mathbf{H}_f \in \mathbb{R}^{\Sigma ^* \times \Sigma ^*}$
to recover information about the weighted automaton computing
$\mathbf{H}_f \in \mathbb{R}^{\Sigma ^* \times \Sigma ^*}$
to recover information about the weighted automaton computing
![]() $f$
.
$f$
.
Theorem 2 (Carlyle and Paz (Reference Carlyle and Paz1971); Fliess (Reference Fliess1974)). A function
![]() $f:\Sigma ^*\rightarrow \mathbb{R}$
is realized by a WFA
$f:\Sigma ^*\rightarrow \mathbb{R}$
is realized by a WFA
![]() $A$
if and only if
$A$
if and only if
![]() $\mathbf{H}_f$
has finite rank. In that case, the rank of
$\mathbf{H}_f$
has finite rank. In that case, the rank of
![]() $\mathbf{H}_f$
corresponds to the minimal number of states of any automaton realizing
$\mathbf{H}_f$
corresponds to the minimal number of states of any automaton realizing
![]() $f$
.
$f$
.
Given a WFA
![]() $A = \langle \boldsymbol{\alpha }, \{ A_a\}_{a \in \Sigma }, \boldsymbol{\beta } \rangle$
, the forward matrix of
$A = \langle \boldsymbol{\alpha }, \{ A_a\}_{a \in \Sigma }, \boldsymbol{\beta } \rangle$
, the forward matrix of
![]() $A$
is the infinite matrix
$A$
is the infinite matrix
![]() $\mathbf{F}_A \in \mathbb{R}^{\Sigma ^* \times n}$
given by
$\mathbf{F}_A \in \mathbb{R}^{\Sigma ^* \times n}$
given by
![]() $\mathbf{F}_A(p,{:}) = \boldsymbol{\alpha } ^\top \mathbf{A}_p$
for any
$\mathbf{F}_A(p,{:}) = \boldsymbol{\alpha } ^\top \mathbf{A}_p$
for any
![]() $p \in \Sigma ^*$
, while the backward matrix of
$p \in \Sigma ^*$
, while the backward matrix of
![]() $A$
is
$A$
is
![]() $\mathbf{B}_A \in \mathbb{R}^{\Sigma ^* \times n}$
, given by
$\mathbf{B}_A \in \mathbb{R}^{\Sigma ^* \times n}$
, given by
![]() $\mathbf{B}_A(s,{:}) = (\mathbf{A}_s \boldsymbol{\beta })^\top$
for any
$\mathbf{B}_A(s,{:}) = (\mathbf{A}_s \boldsymbol{\beta })^\top$
for any
![]() $s \in \Sigma ^*$
. Let
$s \in \Sigma ^*$
. Let
![]() $\mathbf{H}_f$
be the Hankel matrix of
$\mathbf{H}_f$
be the Hankel matrix of
![]() $f$
, its forward-backward (FB) factorization is:
$f$
, its forward-backward (FB) factorization is:
![]() $\mathbf{H}_f = \mathbf{F} \mathbf{B}^\top$
. A WFA with
$\mathbf{H}_f = \mathbf{F} \mathbf{B}^\top$
. A WFA with
![]() $n$
states is reachable if
$n$
states is reachable if
![]() $\textrm{rank}(\mathbf{F}_A)=n$
, while it is observable if
$\textrm{rank}(\mathbf{F}_A)=n$
, while it is observable if
![]() $\textrm{rank}(\mathbf{B}_A)=n$
. A WFA is minimal if it is reachable and observable. If
$\textrm{rank}(\mathbf{B}_A)=n$
. A WFA is minimal if it is reachable and observable. If
![]() $A$
is minimal, the (unique) FB factorization is a rank factorization (Balle et al., Reference Balle, Carreras, Luque and Quattoni2014a).
$A$
is minimal, the (unique) FB factorization is a rank factorization (Balle et al., Reference Balle, Carreras, Luque and Quattoni2014a).
We recall the definition of the singular value automaton, a canonical form for WFAs (Balle et al., Reference Balle, Panangaden and Precup2015).
Definition 3.
Let
![]() $f:\Sigma ^*\rightarrow \mathbb{R}$
be a rational function and suppose
$f:\Sigma ^*\rightarrow \mathbb{R}$
be a rational function and suppose
![]() $\mathbf{H}_f$
admits an SVD,
$\mathbf{H}_f$
admits an SVD,
![]() $\mathbf{H}_f = \mathbf{U} \mathbf{D} \mathbf{V}^{\top }$
. A
singular value automaton
(SVA) for
$\mathbf{H}_f = \mathbf{U} \mathbf{D} \mathbf{V}^{\top }$
. A
singular value automaton
(SVA) for
![]() $f$
is the minimal WFA
$f$
is the minimal WFA
![]() $A$
realizing
$A$
realizing
![]() $f$
such that
$f$
such that
![]() $\mathbf{F}_A=\mathbf{U} \mathbf{D}^{1/2}$
and
$\mathbf{F}_A=\mathbf{U} \mathbf{D}^{1/2}$
and
![]() $\mathbf{B}_A=\mathbf{V}\mathbf{D}^{1/2}$
.
$\mathbf{B}_A=\mathbf{V}\mathbf{D}^{1/2}$
.
The SVA can be computed with an efficient algorithm relying on the following matrices (Balle et al., Reference Balle, Panangaden and Precup2019).
Definition 4.
Let
![]() $f:\Sigma ^*\rightarrow \mathbb{R}$
be a rational function,
$f:\Sigma ^*\rightarrow \mathbb{R}$
be a rational function,
![]() $\mathbf{H}_f = \mathbf{F} \mathbf{B}^\top$
the FB factorization. If the matrices
$\mathbf{H}_f = \mathbf{F} \mathbf{B}^\top$
the FB factorization. If the matrices
![]() $\mathbf{P}=\mathbf{F}^\top \mathbf{F}$
and
$\mathbf{P}=\mathbf{F}^\top \mathbf{F}$
and
![]() $\mathbf{Q}=\mathbf{B}^\top \mathbf{B}$
are well defined (i.e., the inner products of their columns are finite for any column), we call
$\mathbf{Q}=\mathbf{B}^\top \mathbf{B}$
are well defined (i.e., the inner products of their columns are finite for any column), we call
![]() $\mathbf{P}$
the
reachability Gramian
and
$\mathbf{P}$
the
reachability Gramian
and
![]() $\mathbf{Q}$
the
observability Gramian
.
$\mathbf{Q}$
the
observability Gramian
.
If
![]() $A$
is in its SVA form, the Gramians associated with its FB factorization satisfy
$A$
is in its SVA form, the Gramians associated with its FB factorization satisfy
![]() $\mathbf{P}_A = \mathbf{Q}_A = \mathbf{D}$
, where
$\mathbf{P}_A = \mathbf{Q}_A = \mathbf{D}$
, where
![]() $\mathbf{D}$
is the matrix of singular values of the corresponding Hankel matrix. The Gramians can alternatively be characterized and computed (Balle et al., Reference Balle, Panangaden and Precup2019)) using fixed point equations, corresponding to Lyapunov equations when
$\mathbf{D}$
is the matrix of singular values of the corresponding Hankel matrix. The Gramians can alternatively be characterized and computed (Balle et al., Reference Balle, Panangaden and Precup2019)) using fixed point equations, corresponding to Lyapunov equations when
![]() $|\Sigma |=1$
(Lyapunov, Reference Lyapunov1950).
$|\Sigma |=1$
(Lyapunov, Reference Lyapunov1950).
Theorem 5.
Let
![]() $|\Sigma |=1$
,
$|\Sigma |=1$
,
![]() $A= \langle \boldsymbol{\alpha }, \mathbf{A}, \boldsymbol{\beta }\rangle$
a WFA with
$A= \langle \boldsymbol{\alpha }, \mathbf{A}, \boldsymbol{\beta }\rangle$
a WFA with
![]() $n$
states and well-defined Gramians
$n$
states and well-defined Gramians
![]() $\mathbf{P}$
,
$\mathbf{P}$
,
![]() $\mathbf{Q}$
. Then
$\mathbf{Q}$
. Then
![]() $X=\mathbf{P}$
and
$X=\mathbf{P}$
and
![]() $Y=\mathbf{Q}$
solve the equations
$Y=\mathbf{Q}$
solve the equations
![]() $X-\mathbf{A} X\mathbf{A}^{\top }=\boldsymbol{\beta }\boldsymbol{\beta }^{\top }$
and
$X-\mathbf{A} X\mathbf{A}^{\top }=\boldsymbol{\beta }\boldsymbol{\beta }^{\top }$
and
![]() $Y-\mathbf{A}^{\top }Y\mathbf{A}=\boldsymbol{\alpha }\boldsymbol{\alpha }^{\top }$
.
$Y-\mathbf{A}^{\top }Y\mathbf{A}=\boldsymbol{\alpha }\boldsymbol{\alpha }^{\top }$
.
Finally, we recall the definition of generative probabilistic automata (GPA). A WFA
![]() $A= \langle \boldsymbol{\alpha }, \{ A_a\}_{a \in \Sigma }, \boldsymbol{\beta } \rangle$
is a GPA if
$A= \langle \boldsymbol{\alpha }, \{ A_a\}_{a \in \Sigma }, \boldsymbol{\beta } \rangle$
is a GPA if
![]() $f_A(x)\geq 0$
for every
$f_A(x)\geq 0$
for every
![]() $x$
and
$x$
and
![]() $\sum _{x\in \Sigma ^*}f_A(x)=1$
, that is if
$\sum _{x\in \Sigma ^*}f_A(x)=1$
, that is if
![]() $f_A$
computes a probability distribution over
$f_A$
computes a probability distribution over
![]() $\Sigma ^*$
. In general, this class of automata can contain pathological examples having states not connected to any final state. To avoid these cases, we introduce the following property on the spectral radius of the transition matrix.
$\Sigma ^*$
. In general, this class of automata can contain pathological examples having states not connected to any final state. To avoid these cases, we introduce the following property on the spectral radius of the transition matrix.
Definition 6.
Given a WFA
![]() $A= \langle \boldsymbol{\alpha }, \{\mathbf{A}_a\}_{a \in \Sigma }, \boldsymbol{\beta } \rangle$
, let
$A= \langle \boldsymbol{\alpha }, \{\mathbf{A}_a\}_{a \in \Sigma }, \boldsymbol{\beta } \rangle$
, let
![]() $\mathbf{A}=\sum _{a\in \Sigma }\mathbf{A}_{a}$
. The WFA A is
irredundant
if
$\mathbf{A}=\sum _{a\in \Sigma }\mathbf{A}_{a}$
. The WFA A is
irredundant
if
![]() $\rho (\mathbf{A})\lt 1$
.
$\rho (\mathbf{A})\lt 1$
.
2.3 AAK theory
In this section, we introduce the theory of optimal approximation for Hankel operators and complex functions known as AAK theory (Adamyan et al., Reference Adamyan, Arov and Krein1971). A comprehensive presentation of the concepts recalled in this section can be found in Nikol’Skii (Reference Nikol’Skii2002); Peller (Reference Peller2012).
We consider the space of square-integrable complex functions on the unit circle
![]() $\mathscr{L}^{\,2}(\mathbb{T})$
. To avoid any confusion with functions defined over sequences, when dealing with complex function we make explicit the dependence on the complex variable
$\mathscr{L}^{\,2}(\mathbb{T})$
. To avoid any confusion with functions defined over sequences, when dealing with complex function we make explicit the dependence on the complex variable
![]() $z=e^{it}$
. Note that a function
$z=e^{it}$
. Note that a function
![]() $\phi (z) \in \mathscr{L}^{\,2}(\mathbb{T})$
can be represented, using the orthonormal basis
$\phi (z) \in \mathscr{L}^{\,2}(\mathbb{T})$
can be represented, using the orthonormal basis
![]() $\{z^n\}_{n \in \mathbb{Z}}$
, by means of its Fourier series:
$\{z^n\}_{n \in \mathbb{Z}}$
, by means of its Fourier series:
![]() $\phi (z)=\sum _{n \in \mathbb{Z}}\widehat{\phi }(n)z^n$
, with Fourier coefficients
$\phi (z)=\sum _{n \in \mathbb{Z}}\widehat{\phi }(n)z^n$
, with Fourier coefficients
![]() $\widehat{\phi }(n)= \int _{\mathbb{T}}\phi (z) \bar{z}^n dz, \, n \in \mathbb{Z}$
. Thus, we can partition the function space
$\widehat{\phi }(n)= \int _{\mathbb{T}}\phi (z) \bar{z}^n dz, \, n \in \mathbb{Z}$
. Thus, we can partition the function space
![]() $\mathscr{L}^{\,2}(\mathbb{T})$
into two subspaces.
$\mathscr{L}^{\,2}(\mathbb{T})$
into two subspaces.
Definition 7.
The
Hardy space
![]() $\mathscr{H}^{\,\kern1pt2}$
and the
negative Hardy space
$\mathscr{H}^{\,\kern1pt2}$
and the
negative Hardy space
![]() $\mathscr{H}^{\kern1pt\,2}_-$
on
$\mathscr{H}^{\kern1pt\,2}_-$
on
![]() $\mathbb{T}$
are the subspaces of
$\mathbb{T}$
are the subspaces of
![]() $\mathscr{L}^{\,2}(\mathbb{T})$
defined as:
$\mathscr{L}^{\,2}(\mathbb{T})$
defined as:
Interestingly, the elements of the Hardy space can be canonically identified with the set of functions analytic in the unit disc
![]() $\mathbb{D}$
, with the property that the square of their absolute value is integrable on
$\mathbb{D}$
, with the property that the square of their absolute value is integrable on
![]() $\mathbb{T}$
(a proof can be found in Nikol’Skii (Reference Nikol’Skii2002)). Thus, we will make no difference between these functions in the unit disc and their boundary value on the circle. Moreover, we remark that the definition of Hardy space can be generalized for any
$\mathbb{T}$
(a proof can be found in Nikol’Skii (Reference Nikol’Skii2002)). Thus, we will make no difference between these functions in the unit disc and their boundary value on the circle. Moreover, we remark that the definition of Hardy space can be generalized for any
![]() $p$
-th power of the functions’ absolute value, for
$p$
-th power of the functions’ absolute value, for
![]() $0\lt p\leq \infty$
.
$0\lt p\leq \infty$
.
We define Hankel operators in the Hardy spaces.
Definition 8.
Let
![]() $\phi (z)$
be a function in the space
$\phi (z)$
be a function in the space
![]() $\mathscr{L}^{\,2}(\mathbb{T})$
. A
Hankel operator
is an operator
$\mathscr{L}^{\,2}(\mathbb{T})$
. A
Hankel operator
is an operator
![]() $H_{\phi }:\mathscr{H}^{\kern1pt\,2} \rightarrow \mathscr{H}^{\kern1pt\,2}_-$
defined by
$H_{\phi }:\mathscr{H}^{\kern1pt\,2} \rightarrow \mathscr{H}^{\kern1pt\,2}_-$
defined by
![]() $ H_{\phi }f(z)=\mathbb{P}_-\phi f(z)$
, where
$ H_{\phi }f(z)=\mathbb{P}_-\phi f(z)$
, where
![]() $\mathbb{P}_-$
is the orthogonal projection from
$\mathbb{P}_-$
is the orthogonal projection from
![]() $ \mathscr{L}^{\,2}(\mathbb{T})$
onto
$ \mathscr{L}^{\,2}(\mathbb{T})$
onto
![]() $\mathscr{H}^{\kern1pt\,2}_-$
. The function
$\mathscr{H}^{\kern1pt\,2}_-$
. The function
![]() $\phi (z)$
is called a
symbol
of the Hankel operator
$\phi (z)$
is called a
symbol
of the Hankel operator
![]() $H_{\phi }$
.
$H_{\phi }$
.
The matrix
![]() $\mathbf{H}_{\phi }$
associated with the Hankel operator
$\mathbf{H}_{\phi }$
associated with the Hankel operator
![]() $H_{\phi }:\mathscr{H}^{\kern1pt\,2} \rightarrow \mathscr{H}^{\kern1pt\,2}_-$
is:
$H_{\phi }:\mathscr{H}^{\kern1pt\,2} \rightarrow \mathscr{H}^{\kern1pt\,2}_-$
is:
 \begin{equation} \mathbf{H}_{\phi }=\left(\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} \widehat{\phi }(-1) & \widehat{\phi }(-2) & \widehat{\phi }(-3) & \dots \\[4pt] \widehat{\phi }(-2) & \widehat{\phi }(-3) & \widehat{\phi }(-4) &\dots \\[4pt] \widehat{\phi }(-3) & \widehat{\phi }(-4) & \widehat{\phi }(-5) &\dots \\[4pt] \vdots & \vdots &\vdots &\ddots \end{array}\right). \end{equation}
\begin{equation} \mathbf{H}_{\phi }=\left(\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} \widehat{\phi }(-1) & \widehat{\phi }(-2) & \widehat{\phi }(-3) & \dots \\[4pt] \widehat{\phi }(-2) & \widehat{\phi }(-3) & \widehat{\phi }(-4) &\dots \\[4pt] \widehat{\phi }(-3) & \widehat{\phi }(-4) & \widehat{\phi }(-5) &\dots \\[4pt] \vdots & \vdots &\vdots &\ddots \end{array}\right). \end{equation}
Note that this matrix satisfies the Hankel property, as each entry only depends on the composition of the corresponding coordinates.
Nehari’s theorem (Nehari, Reference Nehari1957), characterizes bounded Hankel operators and their norm.
Theorem 9 (Nehari (Reference Nehari1957)). Let
![]() $\phi \in \mathscr{L}^{\,2}(\mathbb{T})$
be a symbol of the Hankel operator on Hardy spaces
$\phi \in \mathscr{L}^{\,2}(\mathbb{T})$
be a symbol of the Hankel operator on Hardy spaces
![]() $H_{\phi }:\mathscr{H}^{\kern1pt\,2} \rightarrow \mathscr{H}^{\kern1pt\,2}_-$
. Then,
$H_{\phi }:\mathscr{H}^{\kern1pt\,2} \rightarrow \mathscr{H}^{\kern1pt\,2}_-$
. Then,
![]() $H_{\phi }$
is bounded on
$H_{\phi }$
is bounded on
![]() $\mathscr{H}^{\kern1pt\,2}$
if and only if there exists
$\mathscr{H}^{\kern1pt\,2}$
if and only if there exists
![]() $\psi \in \mathscr{L}^{\,\infty }(\mathbb{T})$
such that
$\psi \in \mathscr{L}^{\,\infty }(\mathbb{T})$
such that
![]() $\widehat{\psi }(m)=\widehat{\phi }(m)$
for all
$\widehat{\psi }(m)=\widehat{\phi }(m)$
for all
![]() $m\lt 0$
. If the conditions above are satisfied, then:
$m\lt 0$
. If the conditions above are satisfied, then:
As a consequence of Theorem 9, if
![]() $H_{\phi }$
is a bounded operator, we can consider without loss of generality
$H_{\phi }$
is a bounded operator, we can consider without loss of generality
![]() $\phi (z) \in \mathscr{L}^{\,\infty }(\mathbb{T})$
. We remark that a Hankel operator has infinitely many different symbols, since
$\phi (z) \in \mathscr{L}^{\,\infty }(\mathbb{T})$
. We remark that a Hankel operator has infinitely many different symbols, since
![]() $H_{\phi }=H_{\phi +\psi }$
for
$H_{\phi }=H_{\phi +\psi }$
for
![]() $\psi (z) \in \mathscr{H}^{\kern1pt\,\infty }$
.
$\psi (z) \in \mathscr{H}^{\kern1pt\,\infty }$
.
Definition 10.
The complex function
![]() $\phi (z)$
is
rational
if
$\phi (z)$
is
rational
if
![]() $\phi (z)=p(z)/q(z)$
, with
$\phi (z)=p(z)/q(z)$
, with
![]() $p(z)$
and
$p(z)$
and
![]() $q(z)$
polynomials. The rank of
$q(z)$
polynomials. The rank of
![]() $\phi (z)$
is the maximum between the degrees of
$\phi (z)$
is the maximum between the degrees of
![]() $p(z)$
and
$p(z)$
and
![]() $q(z)$
. A rational function is
strictly proper
if the degree of
$q(z)$
. A rational function is
strictly proper
if the degree of
![]() $p(z)$
is strictly smaller than that of
$p(z)$
is strictly smaller than that of
![]() $q(z)$
.
$q(z)$
.
The following result of Kronecker relates finite-rank infinite Hankel matrices to rational functions.
Theorem 11 (Kronecker (Reference Kronecker1881)). Let
![]() $H_{\phi }$
be a bounded Hankel operator with matrix
$H_{\phi }$
be a bounded Hankel operator with matrix
![]() $\mathbf{H}$
. Then
$\mathbf{H}$
. Then
![]() $\mathbf{H}$
has finite rank if and only if
$\mathbf{H}$
has finite rank if and only if
![]() $\mathbb{P}_-\phi$
is a strictly proper rational function. Moreover, the rank of
$\mathbb{P}_-\phi$
is a strictly proper rational function. Moreover, the rank of
![]() $\mathbf{H}$
is equal to the number of poles (with multiplicities) of
$\mathbf{H}$
is equal to the number of poles (with multiplicities) of
![]() $\mathbb{P}_-\phi$
inside the unit disc.
$\mathbb{P}_-\phi$
inside the unit disc.
We are ready to state the main result of Adamyan et al. (Reference Adamyan, Arov and Krein1971). The theorem shows that for infinite dimensional Hankel matrices the constraint of preserving the Hankel property does not affect the achievable approximation error.
Theorem 12 (Adamyan et al. (Reference Adamyan, Arov and Krein1971)). Let
![]() $H_{\phi }$
be a compact Hankel operator of rank
$H_{\phi }$
be a compact Hankel operator of rank
![]() $n$
, matrix
$n$
, matrix
![]() $\mathbf{H}$
and singular numbers
$\mathbf{H}$
and singular numbers
![]() $\sigma _0 \geq \dots \geq \sigma _{n-1}\gt 0$
. Then there exists a unique Hankel operator
$\sigma _0 \geq \dots \geq \sigma _{n-1}\gt 0$
. Then there exists a unique Hankel operator
![]() $H_g$
with matrix
$H_g$
with matrix
![]() $\mathbf{G}$
of rank
$\mathbf{G}$
of rank
![]() $k\lt n$
such that:
$k\lt n$
such that:
We denote with
![]() $\mathscr{R}_k\subset \mathscr{H}^{\kern1pt\,\infty }_-$
the set of strictly proper rational functions of rank
$\mathscr{R}_k\subset \mathscr{H}^{\kern1pt\,\infty }_-$
the set of strictly proper rational functions of rank
![]() $k$
, and we consider the set of functions:
$k$
, and we consider the set of functions:
The proof of the AAK theorem is directly connected with the problem of approximating a bounded function defined on the unit circle. In fact, the theorem can be reformulated in terms of the symbols associated with the Hankel operators.
Theorem 13 (Adamyan et al. (Reference Adamyan, Arov and Krein1971)). Let
![]() $\phi \in \mathscr{L}^{\,\infty }(\mathbb{T})$
. Then there exists a complex function
$\phi \in \mathscr{L}^{\,\infty }(\mathbb{T})$
. Then there exists a complex function
![]() $\psi \in \mathscr{H}^{\kern1pt\,\infty }_k$
such that:
$\psi \in \mathscr{H}^{\kern1pt\,\infty }_k$
such that:
This theorem provides us with an alternative interpretation of singular numbers, relating them to the “smoothness” of the corresponding operator (or symbol). The advantage of this second formulation is that its proof is constructive and tells us how to find the function
![]() $\psi$
. We state as a corollary the critical steps of the proof, that allows us to find the best approximating symbol.
$\psi$
. We state as a corollary the critical steps of the proof, that allows us to find the best approximating symbol.
Corollary 14.
Let
![]() $\phi$
and
$\phi$
and
![]() $\{\boldsymbol{\xi }_k, \boldsymbol{\eta }_k\}$
be a symbol and a
$\{\boldsymbol{\xi }_k, \boldsymbol{\eta }_k\}$
be a symbol and a
![]() $\sigma _k$
-Schmidt pair for
$\sigma _k$
-Schmidt pair for
![]() $H_{\phi }$
. A function
$H_{\phi }$
. A function
![]() $\psi \in \mathscr{L}^{\,\infty }({\mathbb{T}})$
is the best AAK approximation according to Theorem 13
, if and only if:
$\psi \in \mathscr{L}^{\,\infty }({\mathbb{T}})$
is the best AAK approximation according to Theorem 13
, if and only if:
Moreover, the function
![]() $\psi$
does not depend on the particular choice of the pair
$\psi$
does not depend on the particular choice of the pair
![]() $\{\boldsymbol{\xi }_k, \boldsymbol{\eta }_k\}$
.
$\{\boldsymbol{\xi }_k, \boldsymbol{\eta }_k\}$
.
Note that the solutions of Theorem 12 and 13 are strictly related.
Corollary 15.
Let
![]() $\psi \in \mathscr{H}^{\kern1pt\,\infty }_k$
, with
$\psi \in \mathscr{H}^{\kern1pt\,\infty }_k$
, with
![]() $\psi =l+g$
,
$\psi =l+g$
,
![]() $g \in \mathscr{R}_k, \, l \in \mathscr{H}^{\kern1pt\,\infty }$
. If
$g \in \mathscr{R}_k, \, l \in \mathscr{H}^{\kern1pt\,\infty }$
. If
![]() $\psi$
solves Equation
5
, then
$\psi$
solves Equation
5
, then
![]() $H_g$
is the unique Hankel operator from Theorem 12
.
$H_g$
is the unique Hankel operator from Theorem 12
.
In particular, this means that to find the Hankel operator
![]() $H_g$
corresponding to the optimal approximation, we can first obtain
$H_g$
corresponding to the optimal approximation, we can first obtain
![]() $\psi$
by applying Corollary 14. Then, we can extract the rational component
$\psi$
by applying Corollary 14. Then, we can extract the rational component
![]() $g$
of
$g$
of
![]() $\psi$
: this will correspond to a symbol for
$\psi$
: this will correspond to a symbol for
![]() $\mathbf{H}_g$
.
$\mathbf{H}_g$
.
3. AAK Theory and Approximate Minimization
Theorem 2 establishes a correspondence between a given minimal WFA
![]() $A$
with
$A$
with
![]() $n$
states and a Hankel matrix
$n$
states and a Hankel matrix
![]() $\mathbf{H}$
of rank
$\mathbf{H}$
of rank
![]() $n$
. The relation between rank and number of states is what motivates our choice to reformulate the approximate minimization problem as low-rank approximation of the Hankel matrix. The approach that we propose to approximate
$n$
. The relation between rank and number of states is what motivates our choice to reformulate the approximate minimization problem as low-rank approximation of the Hankel matrix. The approach that we propose to approximate
![]() $A$
is to find the minimal WFA corresponding to the Hankel matrix that minimizes
$A$
is to find the minimal WFA corresponding to the Hankel matrix that minimizes
![]() $\mathbf{H}$
optimally in the spectral norm. We recall the fundamental result of Eckart and Young (Reference Eckart and Young1936).
$\mathbf{H}$
optimally in the spectral norm. We recall the fundamental result of Eckart and Young (Reference Eckart and Young1936).
Theorem 16 (Eckart and Young (Reference Eckart and Young1936)). Let
![]() $\mathbf{H}$
be a Hankel matrix corresponding to a compact Hankel operator of rank
$\mathbf{H}$
be a Hankel matrix corresponding to a compact Hankel operator of rank
![]() $n$
, and
$n$
, and
![]() $\sigma _m$
, with
$\sigma _m$
, with
![]() $0\leq m \lt n$
and
$0\leq m \lt n$
and
![]() $\sigma _0 \geq \dots \geq \sigma _{n-1}\gt 0$
, its singular numbers. Then, if
$\sigma _0 \geq \dots \geq \sigma _{n-1}\gt 0$
, its singular numbers. Then, if
![]() $\mathbf{R}$
is a matrix of rank
$\mathbf{R}$
is a matrix of rank
![]() $k$
, we have:
$k$
, we have:
![]() $\|\mathbf{H} - \mathbf{R}\|\geq \sigma _k$
. The equality is attained when
$\|\mathbf{H} - \mathbf{R}\|\geq \sigma _k$
. The equality is attained when
![]() $\mathbf{R}$
corresponds to the truncated SVD of
$\mathbf{R}$
corresponds to the truncated SVD of
![]() $\mathbf{H}$
.
$\mathbf{H}$
.
In the following example, we compute the low-rank approximation of a finite Hankel matrix using the truncated SVD.
Example 1.
We consider the Hankel matrix
![]() $\mathbf{M}\in \mathbb{R}^{3\times 3}$
,
$\mathbf{M}\in \mathbb{R}^{3\times 3}$
,
 \begin{equation*} \mathbf{M}= \left( \begin{array}{c@{\quad}c@{\quad}c} 1 & 2 & 3 \\ 2 & 3 & 1 \\ 3 & 1 & 2 \end{array}\right). \end{equation*}
\begin{equation*} \mathbf{M}= \left( \begin{array}{c@{\quad}c@{\quad}c} 1 & 2 & 3 \\ 2 & 3 & 1 \\ 3 & 1 & 2 \end{array}\right). \end{equation*}
The singular value decomposition of
![]() $\mathbf{M}$
is
$\mathbf{M}$
is
![]() $\mathbf{M}=\mathbf{U}\mathbf{D}\mathbf{V}^{\top }$
, with
$\mathbf{M}=\mathbf{U}\mathbf{D}\mathbf{V}^{\top }$
, with
 \begin{equation*} \mathbf{U}= \left(\begin{array}{c@{\quad}c@{\quad}c} \frac{1}{\sqrt{3}} & \sqrt{\frac{2}{3}} & 0 \\[2pt] \frac{1}{\sqrt{3}} & -\frac{1}{\sqrt{6}} & \frac{1}{\sqrt{2}} \\[2pt] \frac{1}{\sqrt{3}} & -\frac{1}{\sqrt{6}} & -\frac{1}{\sqrt{2}} \end{array}\right), \quad \mathbf{D}= \left(\begin{array}{c@{\quad}c@{\quad}c} 6 & 0 & 0 \\[2pt] 0 & \sqrt{3} & 0 \\[2pt] 0 & 0 & \sqrt{3} \end{array}\right) \quad \mathbf{V}= \left( \begin{array}{c@{\quad}c@{\quad}c} \frac{1}{\sqrt{3}} & -\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{6}} \\[2pt] \frac{1}{\sqrt{3}} & 0 & \sqrt{\frac{2}{3}} \\[2pt] \frac{1}{\sqrt{3}} & \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{6}} \end{array}\right). \end{equation*}
\begin{equation*} \mathbf{U}= \left(\begin{array}{c@{\quad}c@{\quad}c} \frac{1}{\sqrt{3}} & \sqrt{\frac{2}{3}} & 0 \\[2pt] \frac{1}{\sqrt{3}} & -\frac{1}{\sqrt{6}} & \frac{1}{\sqrt{2}} \\[2pt] \frac{1}{\sqrt{3}} & -\frac{1}{\sqrt{6}} & -\frac{1}{\sqrt{2}} \end{array}\right), \quad \mathbf{D}= \left(\begin{array}{c@{\quad}c@{\quad}c} 6 & 0 & 0 \\[2pt] 0 & \sqrt{3} & 0 \\[2pt] 0 & 0 & \sqrt{3} \end{array}\right) \quad \mathbf{V}= \left( \begin{array}{c@{\quad}c@{\quad}c} \frac{1}{\sqrt{3}} & -\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{6}} \\[2pt] \frac{1}{\sqrt{3}} & 0 & \sqrt{\frac{2}{3}} \\[2pt] \frac{1}{\sqrt{3}} & \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{6}} \end{array}\right). \end{equation*}
The rank
![]() $2$
matrix
$2$
matrix
![]() $\mathbf{\overline{M}}$
obtained by truncating the SVD is not Hankel:
$\mathbf{\overline{M}}$
obtained by truncating the SVD is not Hankel:
 \begin{equation*} \mathbf{\overline{M}}= \left( \begin{array}{c@{\quad}c@{\quad}c} 1 & 2 & 3 \\[2pt] \frac{5}{2} & 2 & \frac{3}{2} \\[2pt] \frac{5}{2} & 2 & \frac{3}{2} \end{array}\right). \end{equation*}
\begin{equation*} \mathbf{\overline{M}}= \left( \begin{array}{c@{\quad}c@{\quad}c} 1 & 2 & 3 \\[2pt] \frac{5}{2} & 2 & \frac{3}{2} \\[2pt] \frac{5}{2} & 2 & \frac{3}{2} \end{array}\right). \end{equation*}
It is easy to see that the low-rank approximation of a Hankel matrix obtained by truncating its SVD is not in general a Hankel matrix. This is problematic, since the low-rank approximation needs to be a Hankel matrix in order to correspond to a WFA. On the other hand, we have seen that, by applying AAK theory, we can find the optimal Hankel matrix minimizing the (Hankel) matrix of a Hankel operator in the Hardy spaces. Our objective is to find a way to apply AAK theory to solve the approximate minimization problem of WFAs. To do this, we need an appropriate framework to reformulate this task in terms of Hankel operators and complex functions.
3.1 Defining a Hankel operator: the one-letter assumption
As a first step, we want to understand whether or not a Hankel operator on the Hardy space can be associated with the Hankel matrix of a weighted automaton. To do so, we compare the Hankel matrix
![]() $\mathbf{H}_f$
of a WFA realizing a function
$\mathbf{H}_f$
of a WFA realizing a function
![]() $f$
over an alphabet
$f$
over an alphabet
![]() $\Sigma$
, to the Hankel matrix
$\Sigma$
, to the Hankel matrix
![]() $\mathbf{H}_{\phi }$
of a Hankel operator in the Hardy space:
$\mathbf{H}_{\phi }$
of a Hankel operator in the Hardy space:
 \begin{equation} \mathbf{H}_f = \left(\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} f(\varepsilon ) & f(a) & f(b) &\dots \\[4pt] f(a) & f(aa) & f(ab) &\dots \\[4pt] f(b) &f(ba) & f(bb) &\dots \\[4pt] \vdots & \vdots &\vdots &\ddots \end{array}\right) \quad \quad \mathbf{H}_{\phi }= \left(\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} \widehat{\phi }(-1) & \widehat{\phi }(-2) & \widehat{\phi }(-3) & \dots \\[4pt] \widehat{\phi }(-2) & \widehat{\phi }(-3) & \widehat{\phi }(-4) &\dots \\[4pt] \widehat{\phi }(-3) & \widehat{\phi }(-4) & \widehat{\phi }(-5) &\dots \\[4pt] \vdots & \vdots &\vdots &\ddots \end{array}\right). \end{equation}
\begin{equation} \mathbf{H}_f = \left(\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} f(\varepsilon ) & f(a) & f(b) &\dots \\[4pt] f(a) & f(aa) & f(ab) &\dots \\[4pt] f(b) &f(ba) & f(bb) &\dots \\[4pt] \vdots & \vdots &\vdots &\ddots \end{array}\right) \quad \quad \mathbf{H}_{\phi }= \left(\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} \widehat{\phi }(-1) & \widehat{\phi }(-2) & \widehat{\phi }(-3) & \dots \\[4pt] \widehat{\phi }(-2) & \widehat{\phi }(-3) & \widehat{\phi }(-4) &\dots \\[4pt] \widehat{\phi }(-3) & \widehat{\phi }(-4) & \widehat{\phi }(-5) &\dots \\[4pt] \vdots & \vdots &\vdots &\ddots \end{array}\right). \end{equation}
We remark that the columns and rows of
![]() $\mathbf{H}_f$
are indexed using the letters of the alphabet
$\mathbf{H}_f$
are indexed using the letters of the alphabet
![]() $\Sigma$
:
$\Sigma$
:
while in the case of
![]() $\mathbf{H}_{\phi }$
, the entries are indexed using natural numbers
$\mathbf{H}_{\phi }$
, the entries are indexed using natural numbers
If we think of the intuitive definition of the Hankel property presented in the previous section, we have that it holds in both cases the entries of the matrices only depend on the composition of the coordinate. Note that “composition” means concatenation of letters in the first case, and sum of numbers in the second one. One fundamental difference is that adding natural numbers is a commutative operation, while concatenating letters is not. For example, while for the matrix corresponding to a Hankel operator in the Hardy space we have:
in the case of the WFA’s matrix, this is not true:
This fact reflects in the much stronger structural property satisfied by Hankel of matrices in the Hardy spaces, where the Hankel property implies that the anti-diagonals have constant entries. This property is not reflected by the matrix of an arbitrary WFA, so it is not always possible to associate a Hankel operator to an automaton over an alphabet of arbitrary size, and AAK theory cannot be generally applied. The only case in which concatenation of strings is commutative is when we are restricting our focus on alphabets of one letter. In particular, when
![]() $|\Sigma |=1$
, the set of strings
$|\Sigma |=1$
, the set of strings
![]() $\Sigma ^*$
can be identified with
$\Sigma ^*$
can be identified with
![]() $\mathbb{N}$
. Therefore, the function
$\mathbb{N}$
. Therefore, the function
![]() $f:\Sigma ^* \rightarrow \mathbb{R}$
recognized by a minimal WFA can be rewritten as
$f:\Sigma ^* \rightarrow \mathbb{R}$
recognized by a minimal WFA can be rewritten as
![]() $f:\mathbb{N} \rightarrow \mathbb{R}$
, and the Hankel matrix
$f:\mathbb{N} \rightarrow \mathbb{R}$
, and the Hankel matrix
![]() $\mathbf{H}_f$
associated with it can be interpreted as the matrix of a Hankel operator between sequences
$\mathbf{H}_f$
associated with it can be interpreted as the matrix of a Hankel operator between sequences
![]() $H_f:\ell ^2\rightarrow \ell ^2$
. In this case, the Hankel matrix is defined by
$H_f:\ell ^2\rightarrow \ell ^2$
. In this case, the Hankel matrix is defined by
![]() $\mathbf{H}(i,j)=f(i+j)$
, for
$\mathbf{H}(i,j)=f(i+j)$
, for
![]() $i,j\geq 0$
:
$i,j\geq 0$
:
 \begin{equation*} \mathbf{H}_f= \left(\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} f(0) & f(1) & f(2) & \dots \\[4pt] f(1) & f(2) & f(3) &\dots \\[4pt] f(2) & f(3) & f(4) &\dots \\[4pt] \vdots & \vdots &\vdots &\ddots \end{array}\right). \end{equation*}
\begin{equation*} \mathbf{H}_f= \left(\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} f(0) & f(1) & f(2) & \dots \\[4pt] f(1) & f(2) & f(3) &\dots \\[4pt] f(2) & f(3) & f(4) &\dots \\[4pt] \vdots & \vdots &\vdots &\ddots \end{array}\right). \end{equation*}
Using the Fourier isomorphism, we can interpret
![]() $\mathbf{H}_f$
as the matrix
$\mathbf{H}_f$
as the matrix
![]() $\mathbf{H}_{\phi }$
of a Hankel operator over Hardy spaces, associated with a complex function
$\mathbf{H}_{\phi }$
of a Hankel operator over Hardy spaces, associated with a complex function
![]() $\phi \in \mathscr{L}^{\,2}(\mathbb{T})$
. In particular, we can embed the sequence space
$\phi \in \mathscr{L}^{\,2}(\mathbb{T})$
. In particular, we can embed the sequence space
![]() $\ell ^2$
into
$\ell ^2$
into
![]() $\ell ^2(\mathbb{Z})$
by “duplicating” each vector, that is by associating
$\ell ^2(\mathbb{Z})$
by “duplicating” each vector, that is by associating
![]() $\boldsymbol{\mu }=(\mu _0, \mu _1, \dots )\in \ell ^2$
to
$\boldsymbol{\mu }=(\mu _0, \mu _1, \dots )\in \ell ^2$
to
![]() $\boldsymbol{\mu }^{(2)}=(\dots, \mu _1,\mu _0, \mu _1, \dots )\in \ell ^2(\mathbb{Z})$
. Then, we can use the Fourier isomorphism to map the vector
$\boldsymbol{\mu }^{(2)}=(\dots, \mu _1,\mu _0, \mu _1, \dots )\in \ell ^2(\mathbb{Z})$
. Then, we can use the Fourier isomorphism to map the vector
![]() $\boldsymbol{\mu }^{(2)}\in \ell ^2(\mathbb{Z})$
to the complex function space
$\boldsymbol{\mu }^{(2)}\in \ell ^2(\mathbb{Z})$
to the complex function space
![]() $\mathscr{L}^{\,2}(\mathbb{T})$
. In this way, each vector
$\mathscr{L}^{\,2}(\mathbb{T})$
. In this way, each vector
![]() $\boldsymbol{\mu }\in \ell ^2$
corresponds to two functions in the Hardy spaces:
$\boldsymbol{\mu }\in \ell ^2$
corresponds to two functions in the Hardy spaces:
 \begin{align} &\mu ^-(z)=\sum _{j=0}^{\infty }\boldsymbol{\mu }_j z^{-j-1} \in \mathscr{H}^{\kern1pt\,2}_-, \\[4pt] &\mu ^+(z)=\sum _{j=0}^{\infty } \boldsymbol{\mu }_j z^{j} \in \mathscr{H}^{\kern1pt\,2}.\notag \end{align}
\begin{align} &\mu ^-(z)=\sum _{j=0}^{\infty }\boldsymbol{\mu }_j z^{-j-1} \in \mathscr{H}^{\kern1pt\,2}_-, \\[4pt] &\mu ^+(z)=\sum _{j=0}^{\infty } \boldsymbol{\mu }_j z^{j} \in \mathscr{H}^{\kern1pt\,2}.\notag \end{align}
Moreover, we can derive the relationship between
![]() $f$
and
$f$
and
![]() $\phi$
:
$\phi$
:
 \begin{equation*} \left(\begin {array}{c@{\quad}c@{\quad}c@{\quad}c} f_A(0) & f_A(1) & f_A(2) & \dots \\[4pt] f_A(1) & f_A(2) & f_A(3) &\dots \\[4pt] f_A(2) & f_A(3) & f_A(4) &\dots \\[4pt] \vdots & \vdots &\vdots &\ddots \end {array}\right) =\left(\begin {array}{c@{\quad}c@{\quad}c@{\quad}c} \widehat {\phi }(-1) & \widehat {\phi }(-2) & \widehat {\phi }(-3) & \dots \\[4pt] \widehat {\phi }(-2) & \widehat {\phi }(-3) & \widehat {\phi }(-4) &\dots \\[4pt] \widehat {\phi }(-3) & \widehat {\phi }(-4) & \widehat {\phi }(-5) &\dots \\[4pt] \vdots & \vdots &\vdots &\ddots \end {array}\right). \end{equation*}
\begin{equation*} \left(\begin {array}{c@{\quad}c@{\quad}c@{\quad}c} f_A(0) & f_A(1) & f_A(2) & \dots \\[4pt] f_A(1) & f_A(2) & f_A(3) &\dots \\[4pt] f_A(2) & f_A(3) & f_A(4) &\dots \\[4pt] \vdots & \vdots &\vdots &\ddots \end {array}\right) =\left(\begin {array}{c@{\quad}c@{\quad}c@{\quad}c} \widehat {\phi }(-1) & \widehat {\phi }(-2) & \widehat {\phi }(-3) & \dots \\[4pt] \widehat {\phi }(-2) & \widehat {\phi }(-3) & \widehat {\phi }(-4) &\dots \\[4pt] \widehat {\phi }(-3) & \widehat {\phi }(-4) & \widehat {\phi }(-5) &\dots \\[4pt] \vdots & \vdots &\vdots &\ddots \end {array}\right). \end{equation*}
from which we obtain:
Since we know how to express the function
![]() $f$
with respect to the parameters of the WFA, we can explicitly compute the rational component of the symbol:
$f$
with respect to the parameters of the WFA, we can explicitly compute the rational component of the symbol:
where the last equality holds only if
![]() $\rho (A)\lt 1$
.
$\rho (A)\lt 1$
.
The correspondence between symbol and function computed by a model allows us to reformulate the approximation problem in terms of Hankel operators and functions in the complex space and to apply AAK theory.
We consider the following example, from Balle et al. (Reference Balle, Lacroce, Panangaden, Precup, Rabusseau, Bansal, Merelli and Worrell2021).

Figure 1. Graphical representation of the generative probabilistic automaton described in Example2.
Example 2.
Let
![]() $|\Sigma |=1$
,
$|\Sigma |=1$
,
![]() $\Sigma =\{x\}$
, we consider the WFA
$\Sigma =\{x\}$
, we consider the WFA
![]() $A= \langle \boldsymbol{\alpha }, \mathbf{A}, \boldsymbol{\beta }\rangle$
represented in Figure
1
, with:
$A= \langle \boldsymbol{\alpha }, \mathbf{A}, \boldsymbol{\beta }\rangle$
represented in Figure
1
, with:
 \begin{equation*} \mathbf {A}= \left( \begin {array}{c@{\quad}c} 0 & \frac {1}{2} \\[4pt] \frac {1}{2} & 0 \end {array}\right), \quad \boldsymbol {\alpha }= \left( \begin {array}{c} \frac {\sqrt {3}}{2} \\[4pt] 0 \end {array}\right), \quad \boldsymbol {\beta }= \left( \begin {array}{c} \frac {\sqrt {3}}{2} \\[4pt] 0 \end {array}\right), \end{equation*}
\begin{equation*} \mathbf {A}= \left( \begin {array}{c@{\quad}c} 0 & \frac {1}{2} \\[4pt] \frac {1}{2} & 0 \end {array}\right), \quad \boldsymbol {\alpha }= \left( \begin {array}{c} \frac {\sqrt {3}}{2} \\[4pt] 0 \end {array}\right), \quad \boldsymbol {\beta }= \left( \begin {array}{c} \frac {\sqrt {3}}{2} \\[4pt] 0 \end {array}\right), \end{equation*}
Note that
![]() $A$
is a generative probabilistic automaton. Indeed, we have that
$A$
is a generative probabilistic automaton. Indeed, we have that
-
•
 $f_A(x)\geq 0$
$f_A(x)\geq 0$
-
•
 $\sum _{x\in \Sigma ^*}f_A(x)=1$
,
$\sum _{x\in \Sigma ^*}f_A(x)=1$
,
since the rational function realized by the WFA is defined as:
 \begin{equation*} f_A(x\cdots x)=f_A(k)= \boldsymbol {\alpha }^{\top }\mathbf {A}^k\boldsymbol {\beta }= \begin {cases} 0 &\text {if $k$ is odd} \\ \frac {3}{4}2^{-k} &\text {if $k$ is even} \end {cases} \end{equation*}
\begin{equation*} f_A(x\cdots x)=f_A(k)= \boldsymbol {\alpha }^{\top }\mathbf {A}^k\boldsymbol {\beta }= \begin {cases} 0 &\text {if $k$ is odd} \\ \frac {3}{4}2^{-k} &\text {if $k$ is even} \end {cases} \end{equation*}
where
![]() $k$
corresponds to the string where
$k$
corresponds to the string where
![]() $x$
is repeated
$x$
is repeated
![]() $k$
-times. We remark that
$k$
-times. We remark that
![]() $A$
is minimal and already in its SVA form, with Gramians
$A$
is minimal and already in its SVA form, with Gramians
 \begin{equation} \mathbf{P}=\mathbf{Q}= \left(\begin{array}{c@{\quad}c} \frac{4}{5} & 0 \\[4pt] 0 & \frac{1}{5} \end{array}\right). \end{equation}
\begin{equation} \mathbf{P}=\mathbf{Q}= \left(\begin{array}{c@{\quad}c} \frac{4}{5} & 0 \\[4pt] 0 & \frac{1}{5} \end{array}\right). \end{equation}
The corresponding Hankel matrix, with entries defined as
![]() $\mathbf{H}(i,j)=f(i+j)$
, has rank
$\mathbf{H}(i,j)=f(i+j)$
, has rank
![]() $2$
:
$2$
:
 \begin{equation} \mathbf{H}= \left(\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} f_A(0) & f_A(1) & f_A(2) & \dots \\[4pt] f_A(1) & f_A(2) & f_A(3) &\dots \\[4pt] f_A(2) & f_A(3) & f_A(4) &\dots \\[4pt] \vdots & \vdots &\vdots &\ddots \end{array}\right)= \left(\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} \frac{3}{4} & 0 & \frac{3}{16} & \dots \\[4pt] 0 & \frac{3}{16} & 0 &\dots \\[4pt] \frac{3}{16} & 0 & \frac{3}{64} &\dots \\[4pt] \vdots & \vdots &\vdots &\ddots \end{array}\right). \end{equation}
\begin{equation} \mathbf{H}= \left(\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} f_A(0) & f_A(1) & f_A(2) & \dots \\[4pt] f_A(1) & f_A(2) & f_A(3) &\dots \\[4pt] f_A(2) & f_A(3) & f_A(4) &\dots \\[4pt] \vdots & \vdots &\vdots &\ddots \end{array}\right)= \left(\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} \frac{3}{4} & 0 & \frac{3}{16} & \dots \\[4pt] 0 & \frac{3}{16} & 0 &\dots \\[4pt] \frac{3}{16} & 0 & \frac{3}{64} &\dots \\[4pt] \vdots & \vdots &\vdots &\ddots \end{array}\right). \end{equation}
Now, we can apply the second interpretation of the Hankel matrix and look at it with respect to the symbol, using the definition
![]() $\mathbf{H}(j,k)= \widehat{\phi }(-j-k-1)$
. We have:
$\mathbf{H}(j,k)= \widehat{\phi }(-j-k-1)$
. We have:
 \begin{equation*} \mathbf {H}= \left(\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} \frac {3}{4} & 0 & \frac {3}{16} & \dots \\[4pt] 0 & \frac {3}{16} & 0 &\dots \\[4pt] \frac {3}{16} & 0 & \frac {3}{64} &\dots \\[4pt] \vdots & \vdots &\vdots &\ddots \end {array}\right) =\left(\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} \widehat {\phi }(-1) & \widehat {\phi }(-2) & \widehat {\phi }(-3) & \dots \\[4pt] \widehat {\phi }(-2) & \widehat {\phi }(-3) & \widehat {\phi }(-4) &\dots \\[4pt] \widehat {\phi }(-3) & \widehat {\phi }(-4) & \widehat {\phi }(-5) &\dots \\[4pt] \vdots & \vdots &\vdots &\ddots \end {array}\right). \end{equation*}
\begin{equation*} \mathbf {H}= \left(\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} \frac {3}{4} & 0 & \frac {3}{16} & \dots \\[4pt] 0 & \frac {3}{16} & 0 &\dots \\[4pt] \frac {3}{16} & 0 & \frac {3}{64} &\dots \\[4pt] \vdots & \vdots &\vdots &\ddots \end {array}\right) =\left(\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} \widehat {\phi }(-1) & \widehat {\phi }(-2) & \widehat {\phi }(-3) & \dots \\[4pt] \widehat {\phi }(-2) & \widehat {\phi }(-3) & \widehat {\phi }(-4) &\dots \\[4pt] \widehat {\phi }(-3) & \widehat {\phi }(-4) & \widehat {\phi }(-5) &\dots \\[4pt] \vdots & \vdots &\vdots &\ddots \end {array}\right). \end{equation*}
We can recover the rational component of a symbol, that is the projection of
![]() $\phi$
on the negative Hardy space.
$\phi$
on the negative Hardy space.
Note that this is a complex rational function having degree
![]() $2$
, and it has two poles inside the unit disc at
$2$
, and it has two poles inside the unit disc at
![]() $z=\pm \frac{1}{2}$
(as predicted by Theorem 11). It is important to remark that from the Hankel matrix, we can only recover the negative Fourier coefficients of
$z=\pm \frac{1}{2}$
(as predicted by Theorem 11). It is important to remark that from the Hankel matrix, we can only recover the negative Fourier coefficients of
![]() $\phi$
, meaning only the component of the symbol that belongs to the negative Hardy space.
$\phi$
, meaning only the component of the symbol that belongs to the negative Hardy space.
4. Solving the Approximate Minimization Problem
In this section, we present the theoretical contribution of this paper, a closed-form solution for the approximate minimization problem.
4.1 Assumptions
We briefly list and analyze the assumptions made to solve the approximate minimization problem. A class of automata that automatically satisfies the following properties is that of generative probabilistic automata.
4.1.1 One-letter alphabet
We tackle the approximate minimization problem in the case of automata with real weights, defined over a one-letter alphabet. As discussed before, this assumption is needed in order to apply AAK theory and will hold for the rest of the paper (see Section 3.1 for more details).
4.1.2 SVA form
We assume that the minimal WFA
![]() $A= \langle \boldsymbol{\alpha }, \mathbf{A}, \boldsymbol{\beta }\rangle$
is in SVA form. This assumption is not necessary, as the SVA can be efficiently computed from a WFA satisfying the set of assumptions stated above (Balle et al., Reference Balle, Panangaden and Precup2019). Starting from a WFA in SVA form allows us to obtain results that are representation-independent. Since the alphabet has size one, the Hankel matrix
$A= \langle \boldsymbol{\alpha }, \mathbf{A}, \boldsymbol{\beta }\rangle$
is in SVA form. This assumption is not necessary, as the SVA can be efficiently computed from a WFA satisfying the set of assumptions stated above (Balle et al., Reference Balle, Panangaden and Precup2019). Starting from a WFA in SVA form allows us to obtain results that are representation-independent. Since the alphabet has size one, the Hankel matrix
![]() $\mathbf{H}$
is symmetric. Therefore, if we denote with
$\mathbf{H}$
is symmetric. Therefore, if we denote with
![]() $\lambda _i$
the
$\lambda _i$
the
![]() $i$
-th non-zero eigenvalue of
$i$
-th non-zero eigenvalue of
![]() $\mathbf{H}$
, and we consider the coordinates of
$\mathbf{H}$
, and we consider the coordinates of
![]() $\boldsymbol{\alpha }$
and
$\boldsymbol{\alpha }$
and
![]() $\boldsymbol{\beta }$
, we have that
$\boldsymbol{\beta }$
, we have that
![]() $\boldsymbol{\alpha }_i=\operatorname{sgn}(\lambda _i)\boldsymbol{\beta }_i$
, where
$\boldsymbol{\alpha }_i=\operatorname{sgn}(\lambda _i)\boldsymbol{\beta }_i$
, where
![]() $\operatorname{sgn}(\lambda _i)=\lambda _i/|\lambda _i|$
.
$\operatorname{sgn}(\lambda _i)=\lambda _i/|\lambda _i|$
.
4.1.3 Compactness of the operator
To apply Theorem 12, we need the Hankel operator
![]() $H$
to be compact. To ensure that this condition is satisfied, we study the respective Hankel matrix. In our setting, the Hankel matrix has finite rank (equal to the number of states of the minimal WFA that we are considering). Moreover, the singular values can be computed exactly using the Gramian matrices introduced in Definition4. A finite-rank operator is compact if it is bounded. Therefore, we just need to check that the Hankel operator is bounded. To this extent, Balle et al. (Reference Balle, Panangaden and Precup2019) show that it is enough that the WFA being considered computes a function
$H$
to be compact. To ensure that this condition is satisfied, we study the respective Hankel matrix. In our setting, the Hankel matrix has finite rank (equal to the number of states of the minimal WFA that we are considering). Moreover, the singular values can be computed exactly using the Gramian matrices introduced in Definition4. A finite-rank operator is compact if it is bounded. Therefore, we just need to check that the Hankel operator is bounded. To this extent, Balle et al. (Reference Balle, Panangaden and Precup2019) show that it is enough that the WFA being considered computes a function
![]() $f\in \ell ^2$
. We make the slightly stronger assumption that the transition matrix
$f\in \ell ^2$
. We make the slightly stronger assumption that the transition matrix
![]() $A$
is irredundant, that is that
$A$
is irredundant, that is that
![]() $\rho (\mathbf{A})\lt 1$
, where
$\rho (\mathbf{A})\lt 1$
, where
![]() $\rho$
is the spectral radius. This condition directly implies boundness and the existence of the SVA and the Gramian matrices
$\rho$
is the spectral radius. This condition directly implies boundness and the existence of the SVA and the Gramian matrices
![]() $\mathbf{P}$
and
$\mathbf{P}$
and
![]() $\mathbf{Q}$
, where
$\mathbf{Q}$
, where
![]() $\mathbf{P}=\mathbf{Q}$
and are diagonal matrices (Balle et al., Reference Balle, Panangaden and Precup2019). Moreover, it allows us to compute a closed form for the symbol of a WFA, as seen in Equation 10.
$\mathbf{P}=\mathbf{Q}$
and are diagonal matrices (Balle et al., Reference Balle, Panangaden and Precup2019). Moreover, it allows us to compute a closed form for the symbol of a WFA, as seen in Equation 10.
4.2 Problem formulation
Let
![]() $A= \langle \boldsymbol{\alpha }, \mathbf{A}, \boldsymbol{\beta } \rangle$
be a minimal irredundant WFA with
$A= \langle \boldsymbol{\alpha }, \mathbf{A}, \boldsymbol{\beta } \rangle$
be a minimal irredundant WFA with
![]() $n$
states and real weights, defined over a one-letter alphabet and represented in its SVA form. Let
$n$
states and real weights, defined over a one-letter alphabet and represented in its SVA form. Let
![]() $\mathbf{H}$
be the Hankel matrix of
$\mathbf{H}$
be the Hankel matrix of
![]() $A$
, we denote with
$A$
, we denote with
![]() $\sigma _i$
, for
$\sigma _i$
, for
![]() $0\leq i \lt n$
, the singular numbers. Given a target number of states
$0\leq i \lt n$
, the singular numbers. Given a target number of states
![]() $k\lt n$
, we say that a WFA
$k\lt n$
, we say that a WFA
![]() $\widehat{A}_k$
with
$\widehat{A}_k$
with
![]() $k$
states solves the optimal spectral-norm approximate minimization problem if the Hankel matrix
$k$
states solves the optimal spectral-norm approximate minimization problem if the Hankel matrix
![]() $\mathbf{G}$
of
$\mathbf{G}$
of
![]() $\widehat{A}_k$
satisfies:
$\widehat{A}_k$
satisfies:
Note that the content of the “optimal spectral-norm approximate minimization” is equivalent to the problem solved by Theorem 12, with the exception that here we represent the inputs and outputs of the problem effectively by means of WFAs.
Based on the AAK theory sketched in Section 2.3, we draw the following steps:
-
1. Compute a symbol for the WFA. Given an irredundant WFA on a one-letter alphabet, we consider its Hankel matrix
 $\mathbf{H}$
and the function
$\mathbf{H}$
and the function
 $f$
that it is computing. We use Equation 10 to associate a complex rational function to the WFA.
$f$
that it is computing. We use Equation 10 to associate a complex rational function to the WFA. -
2. Compute the optimal symbol
 $\psi (z)$
using Corollary 14
. The main challenge here is to find a suitable representation for the functions
$\psi (z)$
using Corollary 14
. The main challenge here is to find a suitable representation for the functions
 $\psi (z)$
and
$\psi (z)$
and
 $e(z)=\phi (z)-\psi (z)$
. We define them in terms of two auxiliary WFAs. The key point is to select constraints on their parameters to leverage the properties of weighted automata, while still keeping the formulation general.
$e(z)=\phi (z)-\psi (z)$
. We define them in terms of two auxiliary WFAs. The key point is to select constraints on their parameters to leverage the properties of weighted automata, while still keeping the formulation general. -
3. Extracting the rational component by solving for
 $g(z)$
in Corollary 15
. This step is arguably the most conceptually challenging, as it requires to identify the position of the function’s poles. In fact, we know from Theorem 11 that
$g(z)$
in Corollary 15
. This step is arguably the most conceptually challenging, as it requires to identify the position of the function’s poles. In fact, we know from Theorem 11 that
 $g(z)$
has
$g(z)$
has
 $k$
poles, all inside the unit disc.
$k$
poles, all inside the unit disc. -
4. Find a WFA representation for
 $g(z)$
. Since in Step 2 we parametrized the functions using WFAs, the expression of
$g(z)$
. Since in Step 2 we parametrized the functions using WFAs, the expression of
 $g(z)$
directly reveals the WFA
$g(z)$
directly reveals the WFA
 $\widehat{A}_k$
.
$\widehat{A}_k$
.
4.3 Finding the optimal approximation
We analyze each of the steps detailed above.
4.3.1 Finding a symbol for the WFA
Let
![]() $A= \langle \boldsymbol{\alpha }, \mathbf{A}, \boldsymbol{\beta } \rangle$
be a minimal irredundant WFA with
$A= \langle \boldsymbol{\alpha }, \mathbf{A}, \boldsymbol{\beta } \rangle$
be a minimal irredundant WFA with
![]() $n$
states, already represented in SVA form.
$n$
states, already represented in SVA form.
![]() $A$
realizes a function
$A$
realizes a function
![]() $f: \Sigma ^* \rightarrow \mathbb{R}$
, defined over a one-letter alphabet
$f: \Sigma ^* \rightarrow \mathbb{R}$
, defined over a one-letter alphabet
![]() $\Sigma =\{a\}$
. Let
$\Sigma =\{a\}$
. Let
![]() $\mathbf{H}$
be its Hankel matrix, with corresponding bounded Hankel operator
$\mathbf{H}$
be its Hankel matrix, with corresponding bounded Hankel operator
![]() $H$
, and singular numbers
$H$
, and singular numbers
![]() $\sigma _i$
, for
$\sigma _i$
, for
![]() $0\leq i \lt n$
.
$0\leq i \lt n$
.
As seen in sub-section 3.1, we can associate a complex function to the WFA. In particular, since we are assuming that
![]() $A$
is irredundant, from Equation 10 we obtain an expression for the rational component of the symbol:
$A$
is irredundant, from Equation 10 we obtain an expression for the rational component of the symbol:
4.3.2 Finding the optimal symbol
To find the solution to Theorem 12, we need to first derive the function
![]() $\psi$
from Theorem 13. Therefore, the second step to solve the approximate minimization problem is to find a proper expression for the complex functions
$\psi$
from Theorem 13. Therefore, the second step to solve the approximate minimization problem is to find a proper expression for the complex functions
![]() $\psi$
and
$\psi$
and
![]() $e=\phi -\psi$
described in Theorem 13. Since our objective is to find the WFA corresponding to the optimal approximation, we focus on representing these functions using the parameters of two auxiliary WFAs. We consider a WFA
$e=\phi -\psi$
described in Theorem 13. Since our objective is to find the WFA corresponding to the optimal approximation, we focus on representing these functions using the parameters of two auxiliary WFAs. We consider a WFA
![]() $\widehat{A}=\langle \widehat{\boldsymbol{\alpha }},\widehat{\mathbf{A}},\widehat{\boldsymbol{\beta }}\rangle$
with more than
$\widehat{A}=\langle \widehat{\boldsymbol{\alpha }},\widehat{\mathbf{A}},\widehat{\boldsymbol{\beta }}\rangle$
with more than
![]() $k$
states, such that the automaton
$k$
states, such that the automaton
![]() $E= \langle \boldsymbol{\alpha }_e, \mathbf{A}_e, \boldsymbol{\beta }_e \rangle$
computing the difference between
$E= \langle \boldsymbol{\alpha }_e, \mathbf{A}_e, \boldsymbol{\beta }_e \rangle$
computing the difference between
![]() $A$
and
$A$
and
![]() $\widehat{A}$
is minimal, with:
$\widehat{A}$
is minimal, with:
 \begin{equation} \mathbf{A}_e= \begin{pmatrix} \mathbf{A} & \mathbf{0} \\[4pt] \mathbf{0} & \widehat{\mathbf{A}} \end{pmatrix}, \quad \boldsymbol{\alpha }_e= \begin{pmatrix} \boldsymbol{\alpha } \\[4pt] -\widehat{\boldsymbol{\alpha }} \end{pmatrix}, \quad \boldsymbol{\beta }_e= \begin{pmatrix} \boldsymbol{\beta } \\[4pt] \widehat{\boldsymbol{\beta }} \end{pmatrix}. \end{equation}
\begin{equation} \mathbf{A}_e= \begin{pmatrix} \mathbf{A} & \mathbf{0} \\[4pt] \mathbf{0} & \widehat{\mathbf{A}} \end{pmatrix}, \quad \boldsymbol{\alpha }_e= \begin{pmatrix} \boldsymbol{\alpha } \\[4pt] -\widehat{\boldsymbol{\alpha }} \end{pmatrix}, \quad \boldsymbol{\beta }_e= \begin{pmatrix} \boldsymbol{\beta } \\[4pt] \widehat{\boldsymbol{\beta }} \end{pmatrix}. \end{equation}
Now, given
![]() $C\in \mathscr{H}^{\kern1pt\,\infty }$
, we consider the complex functions:
$C\in \mathscr{H}^{\kern1pt\,\infty }$
, we consider the complex functions:
The idea is that we want to find the parameters of
![]() $\widehat{A}$
that make
$\widehat{A}$
that make
![]() $\psi$
the solution of Theorem 13. By definition,
$\psi$
the solution of Theorem 13. By definition,
![]() $\psi$
is the sum of two components, one that is bounded around the unit circle and one that has
$\psi$
is the sum of two components, one that is bounded around the unit circle and one that has
![]() $k$
poles inside the unit disc (where
$k$
poles inside the unit disc (where
![]() $k$
is the size of the sought approximation). Therefore, there cannot be poles on the unit circle. By looking at the way we defined the function
$k$
is the size of the sought approximation). Therefore, there cannot be poles on the unit circle. By looking at the way we defined the function
![]() $\psi$
, we can see that its poles correspond to the eigenvalues of
$\psi$
, we can see that its poles correspond to the eigenvalues of
![]() $\widehat{\mathbf{A}}$
, counted with their multiplicities. Thus, in order for
$\widehat{\mathbf{A}}$
, counted with their multiplicities. Thus, in order for
![]() $\psi$
to be the solution of Theorem 13,
$\psi$
to be the solution of Theorem 13,
![]() $1$
cannot be an eigenvalue of
$1$
cannot be an eigenvalue of
![]() $\widehat{\mathbf{A}}$
, and the WFA
$\widehat{\mathbf{A}}$
, and the WFA
![]() $\widehat{A}$
needs to have at least
$\widehat{A}$
needs to have at least
![]() $k$
states.
$k$
states.
As remarked in the previous section, the parameters of the automaton
![]() $A$
only encode the negative Fourier coefficients of the symbol. We add
$A$
only encode the negative Fourier coefficients of the symbol. We add
![]() $C$
to the definition of
$C$
to the definition of
![]() $\psi$
to account for the
$\psi$
to account for the
![]() $\mathscr{H}^{\kern1pt\,\infty }$
component when considering the difference
$\mathscr{H}^{\kern1pt\,\infty }$
component when considering the difference
![]() $\phi -\psi$
. In fact, while this component of the symbol does not affect the spectral norm, it plays a role in the computation of the
$\phi -\psi$
. In fact, while this component of the symbol does not affect the spectral norm, it plays a role in the computation of the
![]() $\mathscr{L}^{\,\infty }$
-norm (in Equation 5), so it cannot be entirely dismissed. Nonetheless, we won’t need to find the value of
$\mathscr{L}^{\,\infty }$
-norm (in Equation 5), so it cannot be entirely dismissed. Nonetheless, we won’t need to find the value of
![]() $C$
, as ultimately we are only interested in the WFA’s parameters.
$C$
, as ultimately we are only interested in the WFA’s parameters.
Now that we have an expression for
![]() $\psi$
and
$\psi$
and
![]() $e$
, we can look back at Theorem 13. From this theorem, we know that by definition,
$e$
, we can look back at Theorem 13. From this theorem, we know that by definition,
![]() $\sigma _k^{1}e$
is a unimodular function. This property of
$\sigma _k^{1}e$
is a unimodular function. This property of
![]() $e$
can be used to derive a set of constraints on the parameters of the WFA
$e$
can be used to derive a set of constraints on the parameters of the WFA
![]() $E=\langle \boldsymbol{\alpha }_e, \mathbf{A}_e, \boldsymbol{\beta }_e\rangle$
. In particular, it is possible to use the maximum modulus principle, according to which the maximum modulus of an holomorphic function is attained on the boundary of the domain. To do so, we leverage a result from the control theory literature (Chui and Chen, Reference Chui and Chen1997), that can be easily applied to our setting. In fact, a parallel can be drawn between dynamical systems and automata, by noting that the impulse response of a discrete time-invariant Single-Input-Single-Output SISO system can be parametrized as a WFA over a one-letter alphabet. This allows us to apply a theorem from Chui and Chen (Chui and Chen (Reference Chui and Chen1997), Theorem 6.3) to find two matrices,
$E=\langle \boldsymbol{\alpha }_e, \mathbf{A}_e, \boldsymbol{\beta }_e\rangle$
. In particular, it is possible to use the maximum modulus principle, according to which the maximum modulus of an holomorphic function is attained on the boundary of the domain. To do so, we leverage a result from the control theory literature (Chui and Chen, Reference Chui and Chen1997), that can be easily applied to our setting. In fact, a parallel can be drawn between dynamical systems and automata, by noting that the impulse response of a discrete time-invariant Single-Input-Single-Output SISO system can be parametrized as a WFA over a one-letter alphabet. This allows us to apply a theorem from Chui and Chen (Chui and Chen (Reference Chui and Chen1997), Theorem 6.3) to find two matrices,
![]() $\mathbf{P}_e$
and
$\mathbf{P}_e$
and
![]() $\mathbf{Q}_e$
, satisfying properties similar to those of the Gramians. It is important to notice that, a priori, the controllability and observability Gramians of
$\mathbf{Q}_e$
, satisfying properties similar to those of the Gramians. It is important to notice that, a priori, the controllability and observability Gramians of
![]() $E$
might not be well defined.
$E$
might not be well defined.
Theorem 17 (Chui and Chen (Reference Chui and Chen1997)). Consider the function
![]() $e= \boldsymbol{\alpha }_e^{\top }(z\mathbf{1}-\mathbf{A}_e)^{-1} \boldsymbol{\beta }_e - C$
and the corresponding minimal WFA
$e= \boldsymbol{\alpha }_e^{\top }(z\mathbf{1}-\mathbf{A}_e)^{-1} \boldsymbol{\beta }_e - C$
and the corresponding minimal WFA
![]() $E=\langle \boldsymbol{\alpha }_e, \mathbf{A}_e, \boldsymbol{\beta }_e \rangle$
associated with it.
$E=\langle \boldsymbol{\alpha }_e, \mathbf{A}_e, \boldsymbol{\beta }_e \rangle$
associated with it.
![]() $\sigma _k^{-1}e$
is unimodular if and only if there exists a unique pair of symmetric invertible matrices
$\sigma _k^{-1}e$
is unimodular if and only if there exists a unique pair of symmetric invertible matrices
![]() $\mathbf{P}_e$
and
$\mathbf{P}_e$
and
![]() $\mathbf{Q}_e$
satisfying:
$\mathbf{Q}_e$
satisfying:
-
(1)
 $\mathbf{P}_e-\mathbf{A}_e \mathbf{P}_e \mathbf{A}_e^\top = \boldsymbol{\beta }_e\boldsymbol{\beta }_e^\top$
$\mathbf{P}_e-\mathbf{A}_e \mathbf{P}_e \mathbf{A}_e^\top = \boldsymbol{\beta }_e\boldsymbol{\beta }_e^\top$
-
(2)
 $\mathbf{Q}_e-\mathbf{A}_e^\top \mathbf{Q}_e \mathbf{A}_e = \boldsymbol{\alpha }_e\boldsymbol{\alpha }_e^\top$
$\mathbf{Q}_e-\mathbf{A}_e^\top \mathbf{Q}_e \mathbf{A}_e = \boldsymbol{\alpha }_e\boldsymbol{\alpha }_e^\top$
-
(3)
 $\mathbf{P}_e\mathbf{Q}_e=\sigma ^2_k\mathbf{1}$
$\mathbf{P}_e\mathbf{Q}_e=\sigma ^2_k\mathbf{1}$
We can now derive the parameters of the WFA
![]() $\widehat{A}=\langle \widehat{\boldsymbol{\alpha }},\widehat{\mathbf{A}},\widehat{\boldsymbol{\beta }}\rangle$
that make
$\widehat{A}=\langle \widehat{\boldsymbol{\alpha }},\widehat{\mathbf{A}},\widehat{\boldsymbol{\beta }}\rangle$
that make
![]() $\psi$
the solution of Theorem 13.
$\psi$
the solution of Theorem 13.
Theorem 18.
Let
![]() $A=\langle \boldsymbol{\alpha }, \mathbf{A}, \boldsymbol{\beta } \rangle$
be a minimal WFA with
$A=\langle \boldsymbol{\alpha }, \mathbf{A}, \boldsymbol{\beta } \rangle$
be a minimal WFA with
![]() $n$
states in its SVA form, and let
$n$
states in its SVA form, and let
![]() $\phi = \boldsymbol{\alpha }^{\top }(z\mathbf{1}-\mathbf{A})^{-1}\boldsymbol{\beta }$
be a symbol for its Hankel operator
$\phi = \boldsymbol{\alpha }^{\top }(z\mathbf{1}-\mathbf{A})^{-1}\boldsymbol{\beta }$
be a symbol for its Hankel operator
![]() $H$
. Let
$H$
. Let
![]() $\sigma _k$
be a singular number of multiplicity
$\sigma _k$
be a singular number of multiplicity
![]() $r$
for
$r$
for
![]() $H$
, with:
$H$
, with:
We can partition the Gramian matrices
![]() $\mathbf{P}$
,
$\mathbf{P}$
,
![]() $\mathbf{Q}$
as follows:
$\mathbf{Q}$
as follows:
 \begin{equation} \mathbf{P}=\mathbf{Q}=\begin{pmatrix} \boldsymbol{\Sigma } & \mathbf{0} \\[4pt] \mathbf{0} & \sigma _k\mathbf{1}_r \end{pmatrix}, \end{equation}
\begin{equation} \mathbf{P}=\mathbf{Q}=\begin{pmatrix} \boldsymbol{\Sigma } & \mathbf{0} \\[4pt] \mathbf{0} & \sigma _k\mathbf{1}_r \end{pmatrix}, \end{equation}
where
![]() $\boldsymbol{\Sigma }\in \mathbb{R}^{(n-r)\times (n-r)}$
is the diagonal matrix containing the remaining singular numbers, and partition
$\boldsymbol{\Sigma }\in \mathbb{R}^{(n-r)\times (n-r)}$
is the diagonal matrix containing the remaining singular numbers, and partition
![]() $\mathbf{A}$
,
$\mathbf{A}$
,
![]() $\boldsymbol{\alpha }$
and
$\boldsymbol{\alpha }$
and
![]() $\boldsymbol{\beta }$
to conform with the Gramians:
$\boldsymbol{\beta }$
to conform with the Gramians:
 \begin{equation} \mathbf{A}= \begin{pmatrix} \mathbf{A}_{11} & \mathbf{A}_{12} \\[4pt] \mathbf{A}_{21} & \mathbf{A}_{22} \end{pmatrix},\quad \boldsymbol{\alpha }= \begin{pmatrix} \boldsymbol{\alpha }_1 \\[4pt] \boldsymbol{\alpha }_2 \end{pmatrix},\quad \boldsymbol{\beta }= \begin{pmatrix} \boldsymbol{\beta }_1 \\[4pt] \boldsymbol{\beta }_2 \end{pmatrix}. \end{equation}
\begin{equation} \mathbf{A}= \begin{pmatrix} \mathbf{A}_{11} & \mathbf{A}_{12} \\[4pt] \mathbf{A}_{21} & \mathbf{A}_{22} \end{pmatrix},\quad \boldsymbol{\alpha }= \begin{pmatrix} \boldsymbol{\alpha }_1 \\[4pt] \boldsymbol{\alpha }_2 \end{pmatrix},\quad \boldsymbol{\beta }= \begin{pmatrix} \boldsymbol{\beta }_1 \\[4pt] \boldsymbol{\beta }_2 \end{pmatrix}. \end{equation}
Let
![]() $\mathbf{R}=\sigma _k^2\mathbf{1}_{n-r}-\boldsymbol{\Sigma }^2$
, we denote by
$\mathbf{R}=\sigma _k^2\mathbf{1}_{n-r}-\boldsymbol{\Sigma }^2$
, we denote by
![]() $({\cdot})^{+}$
the Moore-Penrose pseudo-inverse. The function
$({\cdot})^{+}$
the Moore-Penrose pseudo-inverse. The function
![]() $\psi = \widehat{\boldsymbol{\alpha }}^{\top }(z\mathbf{1}-\widehat{\mathbf{A}})^{-1} \widehat{\boldsymbol{\beta }}+C$
is the best approximation of
$\psi = \widehat{\boldsymbol{\alpha }}^{\top }(z\mathbf{1}-\widehat{\mathbf{A}})^{-1} \widehat{\boldsymbol{\beta }}+C$
is the best approximation of
![]() $\phi$
if and only if:
$\phi$
if and only if:
-
• If
 $\boldsymbol{\alpha }_2 \neq \mathbf{0}$
:(19)
$\boldsymbol{\alpha }_2 \neq \mathbf{0}$
:(19) \begin{equation} \begin{cases} \widehat{\boldsymbol{\beta }} = - \widehat{\mathbf{A}}\mathbf{A}_{21}^{\top }(\boldsymbol{\beta }_2^{\top })^{+} \\[4pt] \widehat{\boldsymbol{\alpha }} = \widehat{\mathbf{A}}^{\top }\mathbf{R}\mathbf{A}_{12}(\boldsymbol{\alpha }_2^{\top })^{+}\\[4pt] \widehat{\mathbf{A}}(\mathbf{A}_{11}^{\top }- \mathbf{A}_{21}^{\top }(\boldsymbol{\beta }_2^{\top })^{+}\boldsymbol{\beta }_1^{\top })=\mathbf{1} \end{cases} \end{equation}
\begin{equation} \begin{cases} \widehat{\boldsymbol{\beta }} = - \widehat{\mathbf{A}}\mathbf{A}_{21}^{\top }(\boldsymbol{\beta }_2^{\top })^{+} \\[4pt] \widehat{\boldsymbol{\alpha }} = \widehat{\mathbf{A}}^{\top }\mathbf{R}\mathbf{A}_{12}(\boldsymbol{\alpha }_2^{\top })^{+}\\[4pt] \widehat{\mathbf{A}}(\mathbf{A}_{11}^{\top }- \mathbf{A}_{21}^{\top }(\boldsymbol{\beta }_2^{\top })^{+}\boldsymbol{\beta }_1^{\top })=\mathbf{1} \end{cases} \end{equation}
-
• If
 $\boldsymbol{\alpha }_2=\mathbf{0}$
:(20)
$\boldsymbol{\alpha }_2=\mathbf{0}$
:(20) \begin{equation} \begin{cases} \widehat{\boldsymbol{\beta }} = (\mathbf{1} -\widehat{\mathbf{A}}\mathbf{A}_{11}^{\top })(\boldsymbol{\beta }_1^{\top })^{+}\\[4pt] \widehat{\boldsymbol{\alpha }} =-(\mathbf{R} -\widehat{\mathbf{A}}^{\top }\mathbf{R}\mathbf{A}_{11})(\boldsymbol{\alpha }_1^{\top })^{+}\\[4pt] \widehat{\mathbf{A}}\mathbf{A}_{21}^{\top }=\mathbf{0} \end{cases} \end{equation}
\begin{equation} \begin{cases} \widehat{\boldsymbol{\beta }} = (\mathbf{1} -\widehat{\mathbf{A}}\mathbf{A}_{11}^{\top })(\boldsymbol{\beta }_1^{\top })^{+}\\[4pt] \widehat{\boldsymbol{\alpha }} =-(\mathbf{R} -\widehat{\mathbf{A}}^{\top }\mathbf{R}\mathbf{A}_{11})(\boldsymbol{\alpha }_1^{\top })^{+}\\[4pt] \widehat{\mathbf{A}}\mathbf{A}_{21}^{\top }=\mathbf{0} \end{cases} \end{equation}
Proof.
We prove the first implication of this proof by applying Theorem 17 and by obtaining from it a set of equations allowing us to derive the parameters of the WFA
![]() $\widehat{A}$
. The other direction of the theorem can be easily proved by direct computation.
$\widehat{A}$
. The other direction of the theorem can be easily proved by direct computation.
If
![]() $\psi$
is the optimal approximation of
$\psi$
is the optimal approximation of
![]() $\phi$
, the function
$\phi$
, the function
![]() $\sigma ^{-1}e=\phi -\psi$
is unimodular and from Theorem 17 there exist two symmetric nonsingular matrices
$\sigma ^{-1}e=\phi -\psi$
is unimodular and from Theorem 17 there exist two symmetric nonsingular matrices
![]() $\mathbf{P}_e$
,
$\mathbf{P}_e$
,
![]() $\mathbf{Q}_e$
satisfying the fixed point equations:
$\mathbf{Q}_e$
satisfying the fixed point equations:
and such that
![]() $\mathbf{P}_e\mathbf{Q}_e=\sigma ^2_k\mathbf{1}$
. We can partition
$\mathbf{P}_e\mathbf{Q}_e=\sigma ^2_k\mathbf{1}$
. We can partition
![]() $\mathbf{P}_e$
and
$\mathbf{P}_e$
and
![]() $\mathbf{Q}_e$
according to the definition of
$\mathbf{Q}_e$
according to the definition of
![]() $\mathbf{A}_e$
(see Equation 15):
$\mathbf{A}_e$
(see Equation 15):
 \begin{equation*} \mathbf {P}_e= \begin {pmatrix} \mathbf {P}_{11} & \mathbf {P}_{12} \\ \mathbf {P}_{12}^{\top } & \mathbf {P}_{22} \end {pmatrix},\quad \mathbf {Q}_e= \begin {pmatrix} \mathbf {Q}_{11} & \mathbf {Q}_{12} \\ \mathbf {Q}_{12}^{\top } & \mathbf {Q}_{22} \end {pmatrix}. \end{equation*}
\begin{equation*} \mathbf {P}_e= \begin {pmatrix} \mathbf {P}_{11} & \mathbf {P}_{12} \\ \mathbf {P}_{12}^{\top } & \mathbf {P}_{22} \end {pmatrix},\quad \mathbf {Q}_e= \begin {pmatrix} \mathbf {Q}_{11} & \mathbf {Q}_{12} \\ \mathbf {Q}_{12}^{\top } & \mathbf {Q}_{22} \end {pmatrix}. \end{equation*}
From Equations 21 and 22, we note that
![]() $\mathbf{P}_{11}$
and
$\mathbf{P}_{11}$
and
![]() $\mathbf{Q}_{11}$
correspond to the controllability and observability Gramians of
$\mathbf{Q}_{11}$
correspond to the controllability and observability Gramians of
![]() $A$
:
$A$
:
 \begin{equation*} \mathbf {P}_{11}=\mathbf {Q}_{11}=\mathbf {P}=\begin {pmatrix} \boldsymbol {\Sigma } & \mathbf {0} \\ \mathbf {0} & \sigma _k\mathbf {1} \end {pmatrix}. \end{equation*}
\begin{equation*} \mathbf {P}_{11}=\mathbf {Q}_{11}=\mathbf {P}=\begin {pmatrix} \boldsymbol {\Sigma } & \mathbf {0} \\ \mathbf {0} & \sigma _k\mathbf {1} \end {pmatrix}. \end{equation*}
Moreover, since
![]() $\mathbf{P}_e\mathbf{Q}_e=\sigma _k^2\mathbf{1}$
, we get
$\mathbf{P}_e\mathbf{Q}_e=\sigma _k^2\mathbf{1}$
, we get
![]() $\mathbf{P}_{12}\mathbf{Q}_{12}^{\top }=\sigma _k^2\mathbf{1}-\mathbf{P}^2$
. It follows that
$\mathbf{P}_{12}\mathbf{Q}_{12}^{\top }=\sigma _k^2\mathbf{1}-\mathbf{P}^2$
. It follows that
![]() $\mathbf{P}_{12}\mathbf{Q}_{12}^{\top }$
has rank
$\mathbf{P}_{12}\mathbf{Q}_{12}^{\top }$
has rank
![]() $n-r$
. Without loss of generality we can set
$n-r$
. Without loss of generality we can set
![]() $\dim{\widehat{\mathbf{A}}}=j=n-r$
, and choose an appropriate basis for the state space such that
$\dim{\widehat{\mathbf{A}}}=j=n-r$
, and choose an appropriate basis for the state space such that
![]() $\mathbf{P}_{12}=\begin{pmatrix} \mathbf{1} & \mathbf{0} \end{pmatrix} ^{\top }$
and
$\mathbf{P}_{12}=\begin{pmatrix} \mathbf{1} & \mathbf{0} \end{pmatrix} ^{\top }$
and
![]() $\mathbf{Q}_{12}=\begin{pmatrix} \mathbf{R} & \mathbf{0} \end{pmatrix} ^{\top }$
, with
$\mathbf{Q}_{12}=\begin{pmatrix} \mathbf{R} & \mathbf{0} \end{pmatrix} ^{\top }$
, with
![]() $\mathbf{R}=\sigma _k^2\mathbf{1}-\boldsymbol{\Sigma }^2$
. Once
$\mathbf{R}=\sigma _k^2\mathbf{1}-\boldsymbol{\Sigma }^2$
. Once
![]() $\mathbf{P}_{12}$
and
$\mathbf{P}_{12}$
and
![]() $\mathbf{Q}_{12}$
are fixed, the values of
$\mathbf{Q}_{12}$
are fixed, the values of
![]() $\mathbf{P}_{22}$
and
$\mathbf{P}_{22}$
and
![]() $\mathbf{Q}_{22}$
are automatically determined. We obtain:
$\mathbf{Q}_{22}$
are automatically determined. We obtain:
 \begin{equation} \mathbf{P}_e= \begin{pmatrix} \boldsymbol{\Sigma } & \mathbf{0} & \mathbf{1}\\ \mathbf{0} & \sigma _k\mathbf{1} & \mathbf{0}\\ \mathbf{1} & \mathbf{0} & -\boldsymbol{\Sigma } \mathbf{R}^{-1} \end{pmatrix},\quad \mathbf{Q}_e= \begin{pmatrix} \boldsymbol{\Sigma } & \mathbf{0} & \mathbf{R}\\ \mathbf{0} & \sigma _k\mathbf{1} & \mathbf{0}\\ \mathbf{R} & \mathbf{0} & -\boldsymbol{\Sigma } \mathbf{R} \end{pmatrix}. \end{equation}
\begin{equation} \mathbf{P}_e= \begin{pmatrix} \boldsymbol{\Sigma } & \mathbf{0} & \mathbf{1}\\ \mathbf{0} & \sigma _k\mathbf{1} & \mathbf{0}\\ \mathbf{1} & \mathbf{0} & -\boldsymbol{\Sigma } \mathbf{R}^{-1} \end{pmatrix},\quad \mathbf{Q}_e= \begin{pmatrix} \boldsymbol{\Sigma } & \mathbf{0} & \mathbf{R}\\ \mathbf{0} & \sigma _k\mathbf{1} & \mathbf{0}\\ \mathbf{R} & \mathbf{0} & -\boldsymbol{\Sigma } \mathbf{R} \end{pmatrix}. \end{equation}
Now that we have an expression for the matrices
![]() $\mathbf{P}_e$
and
$\mathbf{P}_e$
and
![]() $\mathbf{Q}_e$
of Theorem 17, we can rewrite the fixed point equations to derive the parameters
$\mathbf{Q}_e$
of Theorem 17, we can rewrite the fixed point equations to derive the parameters
![]() $\widehat{\boldsymbol{\alpha }}$
,
$\widehat{\boldsymbol{\alpha }}$
,
![]() $\widehat{\mathbf{A}}$
and
$\widehat{\mathbf{A}}$
and
![]() $\widehat{\boldsymbol{\beta }}$
. We obtain the following systems:
$\widehat{\boldsymbol{\beta }}$
. We obtain the following systems:
 \begin{equation} \begin{cases} \mathbf{P} -\mathbf{A} \mathbf{P} \mathbf{A}^{\top }= \boldsymbol{\beta }\boldsymbol{\beta }^{\top }\\[4pt] \mathbf{N} -\mathbf{A} \mathbf{N} \widehat{\mathbf{A}}^{\top }= \boldsymbol{\beta }\widehat{\boldsymbol{\beta }}^{\top }\\[4pt] -\boldsymbol{\Sigma } \mathbf{R}^{-1} +\widehat{\mathbf{A}}\boldsymbol{\Sigma } \mathbf{R}^{-1}\widehat{\mathbf{A}}^{\top }={\widehat{\boldsymbol{\beta }}}{\widehat{\boldsymbol{\beta }}}^{\top } \end{cases} \quad \begin{cases} \mathbf{P} -\mathbf{A}^{\top } \mathbf{P} \mathbf{A}= \boldsymbol{\alpha }\boldsymbol{\alpha }^{\top }\\[4pt] \mathbf{M} -\mathbf{A}^{\top } \mathbf{M} \widehat{\mathbf{A}}= -\boldsymbol{\alpha }\widehat{\boldsymbol{\alpha }}^{\top }\\[4pt] -\boldsymbol{\Sigma } \mathbf{R} +\widehat{\mathbf{A}}^{\top }\boldsymbol{\Sigma } \mathbf{R}\widehat{\mathbf{A}}={\widehat{\boldsymbol{\alpha }}}{\widehat{\boldsymbol{\alpha }}}^{\top } \end{cases} \end{equation}
\begin{equation} \begin{cases} \mathbf{P} -\mathbf{A} \mathbf{P} \mathbf{A}^{\top }= \boldsymbol{\beta }\boldsymbol{\beta }^{\top }\\[4pt] \mathbf{N} -\mathbf{A} \mathbf{N} \widehat{\mathbf{A}}^{\top }= \boldsymbol{\beta }\widehat{\boldsymbol{\beta }}^{\top }\\[4pt] -\boldsymbol{\Sigma } \mathbf{R}^{-1} +\widehat{\mathbf{A}}\boldsymbol{\Sigma } \mathbf{R}^{-1}\widehat{\mathbf{A}}^{\top }={\widehat{\boldsymbol{\beta }}}{\widehat{\boldsymbol{\beta }}}^{\top } \end{cases} \quad \begin{cases} \mathbf{P} -\mathbf{A}^{\top } \mathbf{P} \mathbf{A}= \boldsymbol{\alpha }\boldsymbol{\alpha }^{\top }\\[4pt] \mathbf{M} -\mathbf{A}^{\top } \mathbf{M} \widehat{\mathbf{A}}= -\boldsymbol{\alpha }\widehat{\boldsymbol{\alpha }}^{\top }\\[4pt] -\boldsymbol{\Sigma } \mathbf{R} +\widehat{\mathbf{A}}^{\top }\boldsymbol{\Sigma } \mathbf{R}\widehat{\mathbf{A}}={\widehat{\boldsymbol{\alpha }}}{\widehat{\boldsymbol{\alpha }}}^{\top } \end{cases} \end{equation}
where
 $\mathbf{N}= \begin{pmatrix} \mathbf{1} \\ \mathbf{0} \end{pmatrix}$
and
$\mathbf{N}= \begin{pmatrix} \mathbf{1} \\ \mathbf{0} \end{pmatrix}$
and
 $\mathbf{M}= \begin{pmatrix} \mathbf{R} \\ \mathbf{0} \end{pmatrix}$
.
$\mathbf{M}= \begin{pmatrix} \mathbf{R} \\ \mathbf{0} \end{pmatrix}$
.
We can rewrite the second equation of each system as follows:
 \begin{equation} \begin{cases} \mathbf{1} -\mathbf{A}_{11} \widehat{\mathbf{A}}^{\top }= \boldsymbol{\beta }_1\widehat{\boldsymbol{\beta }}^{\top }\\[4pt] -\mathbf{A}_{21}\widehat{\mathbf{A}}^{\top }=\boldsymbol{\beta }_2\widehat{\boldsymbol{\beta }}^{\top } \end{cases} \quad \begin{cases} \mathbf{R} -\mathbf{A}_{11}^{\top } \mathbf{R} \widehat{\mathbf{A}}=-\boldsymbol{\alpha }_1\widehat{\boldsymbol{\alpha }}^{\top }\\[4pt] \widehat{\mathbf{A}}^{\top }\mathbf{R}\mathbf{A}_{12}=\widehat{\boldsymbol{\alpha }}\boldsymbol{\alpha }_2^{\top } \end{cases} \end{equation}
\begin{equation} \begin{cases} \mathbf{1} -\mathbf{A}_{11} \widehat{\mathbf{A}}^{\top }= \boldsymbol{\beta }_1\widehat{\boldsymbol{\beta }}^{\top }\\[4pt] -\mathbf{A}_{21}\widehat{\mathbf{A}}^{\top }=\boldsymbol{\beta }_2\widehat{\boldsymbol{\beta }}^{\top } \end{cases} \quad \begin{cases} \mathbf{R} -\mathbf{A}_{11}^{\top } \mathbf{R} \widehat{\mathbf{A}}=-\boldsymbol{\alpha }_1\widehat{\boldsymbol{\alpha }}^{\top }\\[4pt] \widehat{\mathbf{A}}^{\top }\mathbf{R}\mathbf{A}_{12}=\widehat{\boldsymbol{\alpha }}\boldsymbol{\alpha }_2^{\top } \end{cases} \end{equation}
If
![]() $\boldsymbol{\alpha }_2 \neq \mathbf{0}$
, then also
$\boldsymbol{\alpha }_2 \neq \mathbf{0}$
, then also
![]() $\boldsymbol{\beta }_2 \neq \mathbf{0}$
(recall that
$\boldsymbol{\beta }_2 \neq \mathbf{0}$
(recall that
![]() $\boldsymbol{\alpha }_i=\operatorname{sgn}(\lambda _i)\boldsymbol{\beta }_i$
), and we have:
$\boldsymbol{\alpha }_i=\operatorname{sgn}(\lambda _i)\boldsymbol{\beta }_i$
), and we have:
 \begin{equation} \begin{cases} \widehat{\boldsymbol{\beta }} = - \widehat{\mathbf{A}}\mathbf{A}_{21}^{\top }(\boldsymbol{\beta }_2^{\top })^{+} \\[4pt] \widehat{\boldsymbol{\alpha }} = \widehat{\mathbf{A}}^{\top }\mathbf{R}\mathbf{A}_{12}(\boldsymbol{\alpha }_2^{\top })^{+}\\[4pt] \widehat{\mathbf{A}}(\mathbf{A}_{11}^{\top }- \mathbf{A}_{21}^{\top }(\boldsymbol{\beta }_2^{\top })^{+}\boldsymbol{\beta }_1^{\top })=\mathbf{1} \end{cases} \end{equation}
\begin{equation} \begin{cases} \widehat{\boldsymbol{\beta }} = - \widehat{\mathbf{A}}\mathbf{A}_{21}^{\top }(\boldsymbol{\beta }_2^{\top })^{+} \\[4pt] \widehat{\boldsymbol{\alpha }} = \widehat{\mathbf{A}}^{\top }\mathbf{R}\mathbf{A}_{12}(\boldsymbol{\alpha }_2^{\top })^{+}\\[4pt] \widehat{\mathbf{A}}(\mathbf{A}_{11}^{\top }- \mathbf{A}_{21}^{\top }(\boldsymbol{\beta }_2^{\top })^{+}\boldsymbol{\beta }_1^{\top })=\mathbf{1} \end{cases} \end{equation}
with
![]() $(\boldsymbol{\alpha }_2^{\top })^{+}=\frac{\boldsymbol{\alpha }_2}{\boldsymbol{\alpha }_2^{\top }\boldsymbol{\alpha }_2}$
and
$(\boldsymbol{\alpha }_2^{\top })^{+}=\frac{\boldsymbol{\alpha }_2}{\boldsymbol{\alpha }_2^{\top }\boldsymbol{\alpha }_2}$
and
![]() $(\boldsymbol{\beta }_2^{\top })^{+}=\frac{\boldsymbol{\beta }_2}{\boldsymbol{\beta }_2^{\top }\boldsymbol{\beta }_2}$
.
$(\boldsymbol{\beta }_2^{\top })^{+}=\frac{\boldsymbol{\beta }_2}{\boldsymbol{\beta }_2^{\top }\boldsymbol{\beta }_2}$
.
If
![]() $\boldsymbol{\alpha }_2=\mathbf{0}$
, we have
$\boldsymbol{\alpha }_2=\mathbf{0}$
, we have
![]() $\widehat{\mathbf{A}}\mathbf{A}_{21}^{\top }=\mathbf{0}$
, in which case we obtain the following set of solutions:
$\widehat{\mathbf{A}}\mathbf{A}_{21}^{\top }=\mathbf{0}$
, in which case we obtain the following set of solutions:
 \begin{equation} \begin{cases} \widehat{\boldsymbol{\beta }} = (\mathbf{1} -\widehat{\mathbf{A}}\mathbf{A}_{11}^{\top })(\boldsymbol{\beta }_1^{\top })^{+}\\[4pt] \widehat{\boldsymbol{\alpha }} =-(\mathbf{R} -\widehat{\mathbf{A}}^{\top }\mathbf{R}\mathbf{A}_{11})(\boldsymbol{\alpha }_1^{\top })^{+}\\[4pt] \widehat{\mathbf{A}}\mathbf{A}_{21}^{\top }=\mathbf{0} \end{cases}. \end{equation}
\begin{equation} \begin{cases} \widehat{\boldsymbol{\beta }} = (\mathbf{1} -\widehat{\mathbf{A}}\mathbf{A}_{11}^{\top })(\boldsymbol{\beta }_1^{\top })^{+}\\[4pt] \widehat{\boldsymbol{\alpha }} =-(\mathbf{R} -\widehat{\mathbf{A}}^{\top }\mathbf{R}\mathbf{A}_{11})(\boldsymbol{\alpha }_1^{\top })^{+}\\[4pt] \widehat{\mathbf{A}}\mathbf{A}_{21}^{\top }=\mathbf{0} \end{cases}. \end{equation}
This completes the proof of the first implication. The other direction of the proof can be verified by direct computation by first obtaining the matrices
![]() $\mathbf{P}_e$
and
$\mathbf{P}_e$
and
![]() $\mathbf{Q}_e$
, and then showing that they are symmetric, invertible, and satisfy the set of equations of Theorem 17, hence proving that
$\mathbf{Q}_e$
, and then showing that they are symmetric, invertible, and satisfy the set of equations of Theorem 17, hence proving that
![]() $\sigma _k^{-1}e$
is unimodular.
$\sigma _k^{-1}e$
is unimodular.
We remark that, when
![]() $\boldsymbol{\alpha }_2=0$
, the solution returned by the algorithm will depend on the size of the original automaton and the target approximation. Specifically,
$\boldsymbol{\alpha }_2=0$
, the solution returned by the algorithm will depend on the size of the original automaton and the target approximation. Specifically,
![]() $\widehat{\mathbf{A}}$
has size
$\widehat{\mathbf{A}}$
has size
![]() $(n-r)\times (n-r)$
, while
$(n-r)\times (n-r)$
, while
![]() $\mathbf{A}_{21}^{\top }$
is
$\mathbf{A}_{21}^{\top }$
is
![]() $(n-r)\times r$
, so the system of equations corresponding to
$(n-r)\times r$
, so the system of equations corresponding to
![]() $\widehat{\mathbf{A}}\mathbf{A}_{21}^{\top }=\mathbf{0}$
is underdetermined if
$\widehat{\mathbf{A}}\mathbf{A}_{21}^{\top }=\mathbf{0}$
is underdetermined if
![]() $r\lt \frac{n}{2}$
, in which case we obtain the solutions in Equation 20, with
$r\lt \frac{n}{2}$
, in which case we obtain the solutions in Equation 20, with
![]() $\widehat{\mathbf{A}}\neq \mathbf{0}$
. On the other hand, if
$\widehat{\mathbf{A}}\neq \mathbf{0}$
. On the other hand, if
![]() $r\geq \frac{n}{2}$
, that is if the multiplicity of the singular number
$r\geq \frac{n}{2}$
, that is if the multiplicity of the singular number
![]() $\sigma _k$
is more than half the size of the original WFA, the system might not have any solution unless
$\sigma _k$
is more than half the size of the original WFA, the system might not have any solution unless
![]() $\widehat{\mathbf{A}}=\mathbf{0}$
(or unless
$\widehat{\mathbf{A}}=\mathbf{0}$
(or unless
![]() $\mathbf{A}_{21}$
was zero to begin with). In this setting, the method proposed returns
$\mathbf{A}_{21}$
was zero to begin with). In this setting, the method proposed returns
![]() $\widehat{\mathbf{A}}=\mathbf{0}$
. In the (rare) case in which the algorithm returns
$\widehat{\mathbf{A}}=\mathbf{0}$
. In the (rare) case in which the algorithm returns
![]() $\widehat{\mathbf{A}}=\mathbf{0}$
, an alternative and preferable approach is to search for an approximation of size
$\widehat{\mathbf{A}}=\mathbf{0}$
, an alternative and preferable approach is to search for an approximation of size
![]() $k-1$
or
$k-1$
or
![]() $k+1$
. This way, the multiplicity
$k+1$
. This way, the multiplicity
![]() $r$
of the singular number
$r$
of the singular number
![]() $\sigma _k$
is such that
$\sigma _k$
is such that
![]() $r\lt \frac{n}{2}$
, and the system in Equation 27 is underdetermined.
$r\lt \frac{n}{2}$
, and the system in Equation 27 is underdetermined.
Theorem 18 provides us with a way to compute the coefficients of the function
![]() $\psi$
solving Theorem 13. It is important to notice that the WFA
$\psi$
solving Theorem 13. It is important to notice that the WFA
![]() $A_k$
is not necessarily the best approximation we are looking for. Intuitively, the problem is that it might be too big, as irredundancy is not guaranteed by the system of equations (while we know from AAK theory that the best approximation corresponds to a bounded operator). Therefore, in these cases we need to “extract” from
$A_k$
is not necessarily the best approximation we are looking for. Intuitively, the problem is that it might be too big, as irredundancy is not guaranteed by the system of equations (while we know from AAK theory that the best approximation corresponds to a bounded operator). Therefore, in these cases we need to “extract” from
![]() $A_k$
a smaller WFA of size
$A_k$
a smaller WFA of size
![]() $k$
. We do this by extracting the component of the function
$k$
. We do this by extracting the component of the function
![]() $\psi$
that belongs to the negative Hardy space.
$\psi$
that belongs to the negative Hardy space.
4.3.3 Extracting the rational component
The objective of this section is to “isolate” the function
![]() $g\in \mathscr{R}_k$
, that is the rational component of
$g\in \mathscr{R}_k$
, that is the rational component of
![]() $\psi$
. To do this, we study the position of the poles of
$\psi$
. To do this, we study the position of the poles of
![]() $\psi$
. In fact, we know from Theorem 11 that the poles of a strictly proper rational function lie inside the unit disc. As noted before, the key to solving our problem is the way we parametrized the functions. We defined
$\psi$
. In fact, we know from Theorem 11 that the poles of a strictly proper rational function lie inside the unit disc. As noted before, the key to solving our problem is the way we parametrized the functions. We defined
![]() $\psi$
so that its poles correspond to the eigenvalues of
$\psi$
so that its poles correspond to the eigenvalues of
![]() $\widehat{A}$
. Therefore, we study the eigenvalues of
$\widehat{A}$
. Therefore, we study the eigenvalues of
![]() $\widehat{\mathbf{A}}$
using the following auxiliary result from Ostrowski and Schneider (Reference Ostrowski and Schneider1962). A proof of this theorem can be found in Wimmer (Reference Wimmer1973).
$\widehat{\mathbf{A}}$
using the following auxiliary result from Ostrowski and Schneider (Reference Ostrowski and Schneider1962). A proof of this theorem can be found in Wimmer (Reference Wimmer1973).
Theorem 19 (Ostrowski and Schneider (Reference Ostrowski and Schneider1962)). Let
![]() $|\Sigma |=1$
, and let
$|\Sigma |=1$
, and let
![]() $\mathbf{P}$
be a solution to the fixed point equation
$\mathbf{P}$
be a solution to the fixed point equation
![]() $X-\mathbf{A} X\mathbf{A}^{\top }=\boldsymbol{\beta }\boldsymbol{\beta }^{\top }$
for the WFA
$X-\mathbf{A} X\mathbf{A}^{\top }=\boldsymbol{\beta }\boldsymbol{\beta }^{\top }$
for the WFA
![]() $A=\langle \boldsymbol{\alpha }, \mathbf{A}, \boldsymbol{\beta } \rangle$
. If
$A=\langle \boldsymbol{\alpha }, \mathbf{A}, \boldsymbol{\beta } \rangle$
. If
![]() $A$
is reachable, then:
$A$
is reachable, then:
-
• The number of eigenvalues
 $\lambda$
of
$\lambda$
of
 $\mathbf{A}$
such that
$\mathbf{A}$
such that
 $|\lambda |\lt 1$
is equal to the number of positive eigenvalues of
$|\lambda |\lt 1$
is equal to the number of positive eigenvalues of
 $\mathbf{P}$
.
$\mathbf{P}$
. -
• The number of eigenvalues
 $\lambda$
of
$\lambda$
of
 $\mathbf{A}$
such that
$\mathbf{A}$
such that
 $|\lambda |\gt 1$
is equal to the number of negative eigenvalues of
$|\lambda |\gt 1$
is equal to the number of negative eigenvalues of
 $\mathbf{P}$
.
$\mathbf{P}$
.
After a change of basis (that we detail in Section 5 with the approximation algorithm), we can rewrite
![]() $\widehat{\mathbf{A}}$
in block-diagonal form:
$\widehat{\mathbf{A}}$
in block-diagonal form:
 \begin{equation} \widehat{\mathbf{A}}= \begin{pmatrix} \widehat{\mathbf{A}}_+ & \mathbf{0} \\ \mathbf{0} & \widehat{\mathbf{A}}_- \end{pmatrix} \end{equation}
\begin{equation} \widehat{\mathbf{A}}= \begin{pmatrix} \widehat{\mathbf{A}}_+ & \mathbf{0} \\ \mathbf{0} & \widehat{\mathbf{A}}_- \end{pmatrix} \end{equation}
where the modulus of the eigenvalues of
![]() $\widehat{\mathbf{A}}_+$
(resp.
$\widehat{\mathbf{A}}_+$
(resp.
![]() $\widehat{\mathbf{A}}_-$
) is smaller (resp. greater) than one. We then apply the same change of coordinates on
$\widehat{\mathbf{A}}_-$
) is smaller (resp. greater) than one. We then apply the same change of coordinates on
![]() $\widehat{\boldsymbol{\alpha }}$
and
$\widehat{\boldsymbol{\alpha }}$
and
![]() $\widehat{\boldsymbol{\beta }}$
.
$\widehat{\boldsymbol{\beta }}$
.
We can finally find the rational component of the function
![]() $\psi$
, that is the function
$\psi$
, that is the function
![]() $g$
from Corollary 15 necessary to solve that approximate minimization problem.
$g$
from Corollary 15 necessary to solve that approximate minimization problem.
Theorem 20.
Let
![]() $\widehat{\mathbf{A}}_+$
be as in Equation
28
, and
$\widehat{\mathbf{A}}_+$
be as in Equation
28
, and
![]() $\widehat{\boldsymbol{\alpha }}_+, \widehat{\boldsymbol{\beta }}_+$
obtained applying the same change of basis. The rational component of
$\widehat{\boldsymbol{\alpha }}_+, \widehat{\boldsymbol{\beta }}_+$
obtained applying the same change of basis. The rational component of
![]() $\psi$
is the function
$\psi$
is the function
![]() $g= \widehat{\boldsymbol{\alpha }}_+^{\top }(z\mathbf{1}-\widehat{\mathbf{A}}_+)^{-1}\widehat{\boldsymbol{\beta }}_+$
.
$g= \widehat{\boldsymbol{\alpha }}_+^{\top }(z\mathbf{1}-\widehat{\mathbf{A}}_+)^{-1}\widehat{\boldsymbol{\beta }}_+$
.
Proof.
Clearly
![]() $\psi =g+ l$
, with
$\psi =g+ l$
, with
![]() $l=\widehat{\boldsymbol{\alpha }}_-^{\top }(z\mathbf{1}-\widehat{\mathbf{A}}_-)^{-1}\widehat{\boldsymbol{\beta }}_-$
,
$l=\widehat{\boldsymbol{\alpha }}_-^{\top }(z\mathbf{1}-\widehat{\mathbf{A}}_-)^{-1}\widehat{\boldsymbol{\beta }}_-$
,
![]() $l \in \mathscr{H}^{\kern1pt\,\infty }$
. To conclude the proof we need to show that
$l \in \mathscr{H}^{\kern1pt\,\infty }$
. To conclude the proof we need to show that
![]() $g$
has
$g$
has
![]() $k$
poles inside the unit disc, and that therefore it has rank
$k$
poles inside the unit disc, and that therefore it has rank
![]() $k$
. We do this by studying the modulus of the eigenvalues of
$k$
. We do this by studying the modulus of the eigenvalues of
![]() $\widehat{\mathbf{A}}_+$
.
$\widehat{\mathbf{A}}_+$
.
Since
![]() $E$
is minimal,
$E$
is minimal,
![]() $\widehat{A}$
is reachable by definition, so we can use Theorem 19 and solve the problem by directly examining the eigenvalues of
$\widehat{A}$
is reachable by definition, so we can use Theorem 19 and solve the problem by directly examining the eigenvalues of
![]() $-\boldsymbol{\Sigma } \mathbf{R}$
. From the proof of Theorem 18, we have
$-\boldsymbol{\Sigma } \mathbf{R}$
. From the proof of Theorem 18, we have
![]() $-\boldsymbol{\Sigma } \mathbf{R}=\boldsymbol{\Sigma }(\boldsymbol{\Sigma }^2-\sigma ^2_k\mathbf{1})$
, where
$-\boldsymbol{\Sigma } \mathbf{R}=\boldsymbol{\Sigma }(\boldsymbol{\Sigma }^2-\sigma ^2_k\mathbf{1})$
, where
![]() $\boldsymbol \Sigma$
is the diagonal matrix having as elements the singular numbers of
$\boldsymbol \Sigma$
is the diagonal matrix having as elements the singular numbers of
![]() $H$
different from
$H$
different from
![]() $\sigma _k$
. It follows that
$\sigma _k$
. It follows that
![]() $-\boldsymbol{\Sigma } \mathbf{R}$
has only
$-\boldsymbol{\Sigma } \mathbf{R}$
has only
![]() $k$
strictly positive eigenvalues, and
$k$
strictly positive eigenvalues, and
![]() $\widehat{\mathbf{A}}$
has
$\widehat{\mathbf{A}}$
has
![]() $k$
eigenvalues with modulus smaller than
$k$
eigenvalues with modulus smaller than
![]() $1$
. Thus,
$1$
. Thus,
![]() $\widehat{\mathbf{A}}_+$
has
$\widehat{\mathbf{A}}_+$
has
![]() $k$
eigenvalues, corresponding to the poles of
$k$
eigenvalues, corresponding to the poles of
![]() $g$
.
$g$
.
4.3.4 Solving the approximation problem
Now that we have found the rational function
![]() $g$
, a symbol for the operator that solves Theorem 12, we need to find the parameters of
$g$
, a symbol for the operator that solves Theorem 12, we need to find the parameters of
![]() $\widehat{A}_k$
, the WFA corresponding to the optimal approximation. These are directly revealed by the expression of
$\widehat{A}_k$
, the WFA corresponding to the optimal approximation. These are directly revealed by the expression of
![]() $g$
, due to the function’s parametrization.
$g$
, due to the function’s parametrization.
Theorem 21.
Let
![]() $A= \langle \boldsymbol{\alpha }, \mathbf{A}, \boldsymbol{\beta } \rangle$
be a minimal WFA with
$A= \langle \boldsymbol{\alpha }, \mathbf{A}, \boldsymbol{\beta } \rangle$
be a minimal WFA with
![]() $n$
states over a one-letter alphabet. Let
$n$
states over a one-letter alphabet. Let
![]() $A$
be in its SVA form. The optimal spectral-norm approximation of rank
$A$
be in its SVA form. The optimal spectral-norm approximation of rank
![]() $k$
is given by the WFA
$k$
is given by the WFA
![]() $\widehat{A}_k= \langle \widehat{\boldsymbol{\alpha }}_+, \widehat{\mathbf{A}}_+, \widehat{\boldsymbol{\beta }}_+ \rangle$
.
$\widehat{A}_k= \langle \widehat{\boldsymbol{\alpha }}_+, \widehat{\mathbf{A}}_+, \widehat{\boldsymbol{\beta }}_+ \rangle$
.
Proof.
From Corollary 15, we know that
![]() $g$
is the rational function associated with the Hankel matrix of the best approximation. Given the correspondence between the Fourier coefficients of
$g$
is the rational function associated with the Hankel matrix of the best approximation. Given the correspondence between the Fourier coefficients of
![]() $g$
and the entries of the matrix, we have:
$g$
and the entries of the matrix, we have:
where
![]() $\bar{f}:\Sigma ^* \rightarrow \mathbb{R}$
is the function computed by
$\bar{f}:\Sigma ^* \rightarrow \mathbb{R}$
is the function computed by
![]() $\widehat{A}_k$
and
$\widehat{A}_k$
and
![]() $\widehat{\boldsymbol{\alpha }}_+, \widehat{\mathbf{A}}_+, \widehat{\boldsymbol{\beta }}_+$
are the parameters.
$\widehat{\boldsymbol{\alpha }}_+, \widehat{\mathbf{A}}_+, \widehat{\boldsymbol{\beta }}_+$
are the parameters.
4.4 Error analysis
Thanks to the use of AAK theory, the method outlined in the previous sections is guaranteed to return the rank
![]() $k$
optimal spectral-norm approximation of a WFA satisfying our assumptions, and the singular number
$k$
optimal spectral-norm approximation of a WFA satisfying our assumptions, and the singular number
![]() $\sigma _k$
provides the error. As noticed before, since the Hankel matrix has finite rank and we can derive the Gramian matrices of the WFA, the singular number corresponding to the error can be computed precisely, even though the Hankel matrix is infinite.
$\sigma _k$
provides the error. As noticed before, since the Hankel matrix has finite rank and we can derive the Gramian matrices of the WFA, the singular number corresponding to the error can be computed precisely, even though the Hankel matrix is infinite.
Similarly to the case of SVA truncation (Balle et al., Reference Balle, Panangaden and Precup2019), owing to the ordering of the singular numbers, the error decreases when
![]() $k$
increases, meaning that allowing
$k$
increases, meaning that allowing
![]() $\widehat{A}_k$
to have more states guarantees a better approximation of
$\widehat{A}_k$
to have more states guarantees a better approximation of
![]() $A$
. Note that the solution we propose is optimal in the spectral norm, but it might not be the case in other norms. Nonetheless, we have the following bound between
$A$
. Note that the solution we propose is optimal in the spectral norm, but it might not be the case in other norms. Nonetheless, we have the following bound between
![]() $\ell ^2$
norm and spectral norm.
$\ell ^2$
norm and spectral norm.
Theorem 22.
Let
![]() $A$
be a minimal WFA computing
$A$
be a minimal WFA computing
![]() $f:\Sigma ^* \rightarrow \mathbb{R}$
, with matrix
$f:\Sigma ^* \rightarrow \mathbb{R}$
, with matrix
![]() $\mathbf{H}$
. Let
$\mathbf{H}$
. Let
![]() $\widehat{A}_k$
be its optimal spectral-norm approximation, computing
$\widehat{A}_k$
be its optimal spectral-norm approximation, computing
![]() $g:\Sigma ^* \rightarrow \mathbb{R}$
, with matrix
$g:\Sigma ^* \rightarrow \mathbb{R}$
, with matrix
![]() $\mathbf{G}$
. Then:
$\mathbf{G}$
. Then:
Proof.
Let
![]() $\mathbf{e}_0=\begin{pmatrix} 1 & 0 & \cdots \end{pmatrix}^{\top }$
,
$\mathbf{e}_0=\begin{pmatrix} 1 & 0 & \cdots \end{pmatrix}^{\top }$
,
![]() $f:\Sigma ^*\rightarrow \mathbb{R}$
,
$f:\Sigma ^*\rightarrow \mathbb{R}$
,
![]() $g:\Sigma ^*\rightarrow \mathbb{R}$
with Hankel matrices
$g:\Sigma ^*\rightarrow \mathbb{R}$
with Hankel matrices
![]() $\mathbf{H}$
and
$\mathbf{H}$
and
![]() $\mathbf{G}$
, respectively. We have:
$\mathbf{G}$
, respectively. We have:
 \begin{align*} \|f-g\|_{\ell ^2} &=\left (\sum _{n=0}^{\infty }|f_n-g_n|^2 \right )^{1/2}\\ &=\|(\mathbf{H}-\mathbf{G}) \mathbf{e}_0\|_{\ell ^2}\\ &\leq \sup _{\|\mathbf{x}\|_{\ell ^2}=1}\|(\mathbf{H}-\mathbf{G})\mathbf{x}\|_{\ell ^2}\\ &=\|\mathbf{H}-\mathbf{G}\|=\sigma _k \end{align*}
\begin{align*} \|f-g\|_{\ell ^2} &=\left (\sum _{n=0}^{\infty }|f_n-g_n|^2 \right )^{1/2}\\ &=\|(\mathbf{H}-\mathbf{G}) \mathbf{e}_0\|_{\ell ^2}\\ &\leq \sup _{\|\mathbf{x}\|_{\ell ^2}=1}\|(\mathbf{H}-\mathbf{G})\mathbf{x}\|_{\ell ^2}\\ &=\|\mathbf{H}-\mathbf{G}\|=\sigma _k \end{align*}
where the second equation follows by definition and by observing that matrix difference is computed entry-wise.
5. Algorithm
We now use the results obtained in the previous sections to define Algorithm1, that we call AAKapproximation.
The algorithm takes as input a target number of states
![]() $k\lt n$
, a minimal irredundant WFA
$k\lt n$
, a minimal irredundant WFA
![]() $A$
$A$
![]() $n$
states and in SVA form, and its Gramian
$n$
states and in SVA form, and its Gramian
![]() $\mathbf{P}$
. We assume
$\mathbf{P}$
. We assume
![]() $\boldsymbol{\alpha }_2 \neq 0$
. If
$\boldsymbol{\alpha }_2 \neq 0$
. If
![]() $\boldsymbol{\alpha }_2 = 0$
, it is enough to substitute the Steps
$\boldsymbol{\alpha }_2 = 0$
, it is enough to substitute the Steps
![]() $4,5,6$
with the analogues from Equation 20. As mentioned in Section 4.1, the constraints on the WFA
$4,5,6$
with the analogues from Equation 20. As mentioned in Section 4.1, the constraints on the WFA
![]() $A$
to be minimal and in SVA form are not essential. In fact, a WFA with
$A$
to be minimal and in SVA form are not essential. In fact, a WFA with
![]() $n$
states can be minimized in time
$n$
states can be minimized in time
![]() $O(n^3)$
(Berstel and Reutenauer, Reference Berstel and Reutenauer2011), and the SVA computed in
$O(n^3)$
(Berstel and Reutenauer, Reference Berstel and Reutenauer2011), and the SVA computed in
![]() $O(n^3)$
(Balle et al., Reference Balle, Panangaden and Precup2019). The algorithm applies the results of Theorem 18 in order to derive the parameters of the optimal WFA. The output of the algorithm is the WFA
$O(n^3)$
(Balle et al., Reference Balle, Panangaden and Precup2019). The algorithm applies the results of Theorem 18 in order to derive the parameters of the optimal WFA. The output of the algorithm is the WFA
![]() $\widehat{A}_k$
corresponding to the unique optimal spectral-norm approximation of
$\widehat{A}_k$
corresponding to the unique optimal spectral-norm approximation of
![]() $A$
.
$A$
.
Algorithm 1: AAK approximation

5.1 Block diagonalization
The algorithm involves a call to Algorithm2, BlockDiagonalize. This algorithm corresponds to the steps necessary to derive the WFA
![]() $\widehat{A}_k$
associated with the rational function
$\widehat{A}_k$
associated with the rational function
![]() $g$
. One way to solve the problem is to compute the Jordan form of the matrix. Unfortunately, this problem is ill-conditioned, so it is not suitable for our algorithmic purposes. Following the steps of Glover (Reference Glover1984), we compute the Schur decomposition, that is we find an orthogonal matrix
$g$
. One way to solve the problem is to compute the Jordan form of the matrix. Unfortunately, this problem is ill-conditioned, so it is not suitable for our algorithmic purposes. Following the steps of Glover (Reference Glover1984), we compute the Schur decomposition, that is we find an orthogonal matrix
![]() $\mathbf{U}$
such that the matrix
$\mathbf{U}$
such that the matrix
![]() $\mathbf{U}^{\top }\widehat{\mathbf{A}}\mathbf{U}$
is upper triangular, with the eigenvalues of
$\mathbf{U}^{\top }\widehat{\mathbf{A}}\mathbf{U}$
is upper triangular, with the eigenvalues of
![]() $\widehat{\mathbf{A}}$
on the diagonal. We obtain:
$\widehat{\mathbf{A}}$
on the diagonal. We obtain:
 \begin{equation} \mathbf{T}=\mathbf{U}^{\top }\widehat{\mathbf{A}}\mathbf{U}= \begin{pmatrix} \widehat{\mathbf{A}}_{+} & \widehat{\mathbf{A}}_{12} \\ \mathbf{0} & \widehat{\mathbf{A}}_{-} \end{pmatrix} \end{equation}
\begin{equation} \mathbf{T}=\mathbf{U}^{\top }\widehat{\mathbf{A}}\mathbf{U}= \begin{pmatrix} \widehat{\mathbf{A}}_{+} & \widehat{\mathbf{A}}_{12} \\ \mathbf{0} & \widehat{\mathbf{A}}_{-} \end{pmatrix} \end{equation}
where the eigenvalues are arranged in increasing order of modulus, and the modulus of those in
![]() $\widehat{\mathbf{A}}_{+}$
(resp.
$\widehat{\mathbf{A}}_{+}$
(resp.
![]() $\widehat{\mathbf{A}}_{-}$
) is smaller (resp. greater) than one. To transform this upper triangular matrix into a block-diagonal one, we use the following result.
$\widehat{\mathbf{A}}_{-}$
) is smaller (resp. greater) than one. To transform this upper triangular matrix into a block-diagonal one, we use the following result.
Theorem 23 (Roth (Reference Roth1952)). Let
![]() $\mathbf{T}$
be the matrix defined in Equation
31
. The matrix
$\mathbf{T}$
be the matrix defined in Equation
31
. The matrix
![]() $\mathbf{X}$
is a solution of the equation
$\mathbf{X}$
is a solution of the equation
![]() $\widehat{\mathbf{A}}_{+}\mathbf{X}- \mathbf{X}\widehat{\mathbf{A}}_{-} +\widehat{\mathbf{A}}_{12}=\mathbf{0}$
if and only if the matrices
$\widehat{\mathbf{A}}_{+}\mathbf{X}- \mathbf{X}\widehat{\mathbf{A}}_{-} +\widehat{\mathbf{A}}_{12}=\mathbf{0}$
if and only if the matrices
 \begin{equation} \mathbf{M}=\begin{pmatrix} \mathbf{1} & \mathbf{X} \\ \mathbf{0} & \mathbf{1} \end{pmatrix}, \quad \text{and} \quad \mathbf{M}^{-1}=\begin{pmatrix} \mathbf{1} & -\mathbf{X} \\ \mathbf{0} & \mathbf{1} \end{pmatrix} \end{equation}
\begin{equation} \mathbf{M}=\begin{pmatrix} \mathbf{1} & \mathbf{X} \\ \mathbf{0} & \mathbf{1} \end{pmatrix}, \quad \text{and} \quad \mathbf{M}^{-1}=\begin{pmatrix} \mathbf{1} & -\mathbf{X} \\ \mathbf{0} & \mathbf{1} \end{pmatrix} \end{equation}
satisfy:
 \begin{equation} \mathbf{M}^{-1}\mathbf{T}\mathbf{M}=\begin{pmatrix} \widehat{\mathbf{A}}_{+} & \mathbf{0} \\ \mathbf{0} & \widehat{\mathbf{A}}_{-} \end{pmatrix}, \end{equation}
\begin{equation} \mathbf{M}^{-1}\mathbf{T}\mathbf{M}=\begin{pmatrix} \widehat{\mathbf{A}}_{+} & \mathbf{0} \\ \mathbf{0} & \widehat{\mathbf{A}}_{-} \end{pmatrix}, \end{equation}
where
![]() $\mathbf{T}$
is the matrix defined in Equation
31
.
$\mathbf{T}$
is the matrix defined in Equation
31
.
Setting
![]() $\boldsymbol{\Gamma }=\begin{pmatrix}\mathbf{1}_k & \mathbf{0} \end{pmatrix}$
we can now derive the rational component of the WFA:
$\boldsymbol{\Gamma }=\begin{pmatrix}\mathbf{1}_k & \mathbf{0} \end{pmatrix}$
we can now derive the rational component of the WFA:
The algorithm BlockDiagonalize corresponds to the implementation of this procedure, and Step
![]() $5$
can be performed using the Bartels-Stewart algorithm (Bartels and Stewart, Reference Bartels and Stewart1972).
$5$
can be performed using the Bartels-Stewart algorithm (Bartels and Stewart, Reference Bartels and Stewart1972).
Algorithm 2: BlockDiagonalize

5.2 Computational cost
The running time of BlockDiagonalize with input a WFA
![]() $\widehat{A}$
with
$\widehat{A}$
with
![]() $(n-r)$
states is thus in
$(n-r)$
states is thus in
![]() $O((n-r)^3)$
, where
$O((n-r)^3)$
, where
![]() $r$
is the multiplicity of the singular value considered. The running time of AAKapproximation for an input WFA
$r$
is the multiplicity of the singular value considered. The running time of AAKapproximation for an input WFA
![]() $\widehat{A}$
with
$\widehat{A}$
with
![]() $n$
states is in
$n$
states is in
![]() $O((n-r)^3)$
. In particular, it is possible to analyze the cost associated with each step of the algorithms (Trefethen and Bau III, Reference Trefethen and Bau1997):
$O((n-r)^3)$
. In particular, it is possible to analyze the cost associated with each step of the algorithms (Trefethen and Bau III, Reference Trefethen and Bau1997):
-
• The product of two
 $n\times n$
matrices can be computed in time
$n\times n$
matrices can be computed in time
 $O(n^3)$
using a standard iterative algorithm.
$O(n^3)$
using a standard iterative algorithm. -
• The inversion of a
 $n\times n$
matrix can be computed in time
$n\times n$
matrix can be computed in time
 $O(n^3)$
using Gauss-Jordan elimination.
$O(n^3)$
using Gauss-Jordan elimination. -
• The computation of the Schur decomposition of a
 $n\times n$
matrix can be done with a two-step algorithm, where each step takes
$n\times n$
matrix can be done with a two-step algorithm, where each step takes
 $O(n^3)$
, using the Hessenberg form of the matrix.
$O(n^3)$
, using the Hessenberg form of the matrix. -
• The Bartels-Stewart algorithm applied to upper triangular matrices to find a matrix of size
 $m\times n$
takes
$m\times n$
takes
 $O(mn^2+nm^2)$
.
$O(mn^2+nm^2)$
.
6. Example
We consider the following weighted finite automaton with three states over a one-letter alphabet, represented in SVA form:
 \begin{equation*} \mathbf {A}= \begin {pmatrix} 0.579 & 0.461 & 0.046 \\ -0.461 & -0.192 & 0.225 \\ 0.046 & -0.225 & -0.387 \end {pmatrix}, \quad \boldsymbol {\alpha }= \begin {pmatrix} 1.650 \\ -0.851 \\ 0.038 \end {pmatrix}, \quad \boldsymbol {\beta }= \begin {pmatrix} 1.650 \\ 0.851 \\ 0.038 \end {pmatrix}, \end{equation*}
\begin{equation*} \mathbf {A}= \begin {pmatrix} 0.579 & 0.461 & 0.046 \\ -0.461 & -0.192 & 0.225 \\ 0.046 & -0.225 & -0.387 \end {pmatrix}, \quad \boldsymbol {\alpha }= \begin {pmatrix} 1.650 \\ -0.851 \\ 0.038 \end {pmatrix}, \quad \boldsymbol {\beta }= \begin {pmatrix} 1.650 \\ 0.851 \\ 0.038 \end {pmatrix}, \end{equation*}
The objective is to find the WFA with two states solving the approximate minimization problem optimally.
We first note that
![]() $\mathbf{A}$
has spectral radius strictly smaller than
$\mathbf{A}$
has spectral radius strictly smaller than
![]() $1$
, having eigenvalues:
$1$
, having eigenvalues:
Therefore, the assumptions listed Section 4.1 are satisfied, and we can apply Theorem 18. We compute the Gramian matrices and obtain, according to the partition in Equation 17, the following matrix:
 \begin{equation*} \mathbf {P}= \mathbf {Q}=\begin {pmatrix} 4.67 & 0 & 0 \\ 0 & 1.79 & 0 \\ 0 & 0 & 0.12 \end {pmatrix}, \end{equation*}
\begin{equation*} \mathbf {P}= \mathbf {Q}=\begin {pmatrix} 4.67 & 0 & 0 \\ 0 & 1.79 & 0 \\ 0 & 0 & 0.12 \end {pmatrix}, \end{equation*}
so that
![]() $\sigma _2^2=0.12$
and:
$\sigma _2^2=0.12$
and:
 \begin{equation*} \boldsymbol {\Sigma }=\begin {pmatrix}4.67 & 0 \\ 0 & 1.79 \end {pmatrix}. \end{equation*}
\begin{equation*} \boldsymbol {\Sigma }=\begin {pmatrix}4.67 & 0 \\ 0 & 1.79 \end {pmatrix}. \end{equation*}
We then proceed by partitioning
![]() $\mathbf{A}$
,
$\mathbf{A}$
,
![]() $\boldsymbol{\alpha }$
and
$\boldsymbol{\alpha }$
and
![]() $\boldsymbol{\beta }$
and obtain:
$\boldsymbol{\beta }$
and obtain:
 \begin{equation*} \mathbf {A}_{11}= \begin {pmatrix} 0.579 & 0.461 \\ -0.461 & -0.192 \end {pmatrix}, \quad \mathbf {A}_{1,2}= \begin {pmatrix} 0.046 \\ 0.225 \end {pmatrix}, \quad \mathbf {A}_{2,1}^{\top }= \begin {pmatrix} 0.046 \\ -0.225 \end {pmatrix}, \quad \mathbf {A}_{22}=-0.387. \end{equation*}
\begin{equation*} \mathbf {A}_{11}= \begin {pmatrix} 0.579 & 0.461 \\ -0.461 & -0.192 \end {pmatrix}, \quad \mathbf {A}_{1,2}= \begin {pmatrix} 0.046 \\ 0.225 \end {pmatrix}, \quad \mathbf {A}_{2,1}^{\top }= \begin {pmatrix} 0.046 \\ -0.225 \end {pmatrix}, \quad \mathbf {A}_{22}=-0.387. \end{equation*}
 \begin{equation*} \boldsymbol {\alpha }_1= \begin {pmatrix} 1.650 \\ -0.851 \end {pmatrix}, \quad \boldsymbol {\beta }_1= \begin {pmatrix} 1.650 \\ 0.851 \end {pmatrix}, \quad \boldsymbol {\alpha }_2=\boldsymbol {\beta }_2=0.038. \end{equation*}
\begin{equation*} \boldsymbol {\alpha }_1= \begin {pmatrix} 1.650 \\ -0.851 \end {pmatrix}, \quad \boldsymbol {\beta }_1= \begin {pmatrix} 1.650 \\ 0.851 \end {pmatrix}, \quad \boldsymbol {\alpha }_2=\boldsymbol {\beta }_2=0.038. \end{equation*}
Since
![]() $\boldsymbol{\alpha }_2\neq 0$
, we can use Equation 19 to find the coefficients of the auxiliary WFA
$\boldsymbol{\alpha }_2\neq 0$
, we can use Equation 19 to find the coefficients of the auxiliary WFA
![]() $\widehat{A}=\langle \widehat{\boldsymbol{\alpha }},\widehat{\mathbf{A}},\widehat{\boldsymbol{\beta }}\rangle$
.
$\widehat{A}=\langle \widehat{\boldsymbol{\alpha }},\widehat{\mathbf{A}},\widehat{\boldsymbol{\beta }}\rangle$
.
We have:
 \begin{align*} &\begin{cases} \widehat{\boldsymbol{\beta }} = - \widehat{\mathbf{A}}\mathbf{A}_{21}^{\top }(\boldsymbol{\beta }_2^{\top })^{+} \\[3pt] \widehat{\boldsymbol{\alpha }} = \widehat{\mathbf{A}}^{\top }\mathbf{R}\mathbf{A}_{12}(\boldsymbol{\alpha }_2^{\top })^{+}\\[3pt] \widehat{\mathbf{A}}(\mathbf{A}_{11}^{\top }- \mathbf{A}_{21}^{\top }(\boldsymbol{\beta }_2^{\top })^{+}\boldsymbol{\beta }_1^{\top })=\mathbf{1} \end{cases}\\ &\begin{cases} \widehat{\boldsymbol{\beta }} = - \widehat{\mathbf{A}}\begin{pmatrix} 0.046 \\ -0.225 \end{pmatrix}(0.038)^{-1} \\[3pt] \widehat{\boldsymbol{\alpha }} = \widehat{\mathbf{A}}^{\top }\left (\begin{pmatrix}0.12 & 0 \\ 0 & 0.12 \end{pmatrix}-\begin{pmatrix}4.67 & 0 \\ 0 & 1.79 \end{pmatrix}^2\right )\begin{pmatrix} 0.046 \\ 0.225 \end{pmatrix}(0.038)^{-1}\\[3pt] \widehat{\mathbf{A}}\left (\begin{pmatrix} 0.579 & 0.461 \\ -0.461 & -0.192 \end{pmatrix}^{\top }- \begin{pmatrix} 0.046 \\ -0.225 \end{pmatrix}(0.038)^{-1}\begin{pmatrix} 1.650 \\ 0.851 \end{pmatrix}^{\top }\right )=\mathbf{1} \end{cases} \end{align*}
\begin{align*} &\begin{cases} \widehat{\boldsymbol{\beta }} = - \widehat{\mathbf{A}}\mathbf{A}_{21}^{\top }(\boldsymbol{\beta }_2^{\top })^{+} \\[3pt] \widehat{\boldsymbol{\alpha }} = \widehat{\mathbf{A}}^{\top }\mathbf{R}\mathbf{A}_{12}(\boldsymbol{\alpha }_2^{\top })^{+}\\[3pt] \widehat{\mathbf{A}}(\mathbf{A}_{11}^{\top }- \mathbf{A}_{21}^{\top }(\boldsymbol{\beta }_2^{\top })^{+}\boldsymbol{\beta }_1^{\top })=\mathbf{1} \end{cases}\\ &\begin{cases} \widehat{\boldsymbol{\beta }} = - \widehat{\mathbf{A}}\begin{pmatrix} 0.046 \\ -0.225 \end{pmatrix}(0.038)^{-1} \\[3pt] \widehat{\boldsymbol{\alpha }} = \widehat{\mathbf{A}}^{\top }\left (\begin{pmatrix}0.12 & 0 \\ 0 & 0.12 \end{pmatrix}-\begin{pmatrix}4.67 & 0 \\ 0 & 1.79 \end{pmatrix}^2\right )\begin{pmatrix} 0.046 \\ 0.225 \end{pmatrix}(0.038)^{-1}\\[3pt] \widehat{\mathbf{A}}\left (\begin{pmatrix} 0.579 & 0.461 \\ -0.461 & -0.192 \end{pmatrix}^{\top }- \begin{pmatrix} 0.046 \\ -0.225 \end{pmatrix}(0.038)^{-1}\begin{pmatrix} 1.650 \\ 0.851 \end{pmatrix}^{\top }\right )=\mathbf{1} \end{cases} \end{align*}
so we get:
 \begin{equation*} \widehat {\mathbf {A}}= \begin {pmatrix} 0.578 & 0.178 \\ -1.221 & -0.169 \end {pmatrix}, \quad \widehat {\boldsymbol {\alpha }}= \begin {pmatrix} 7.105 \\ -1.579 \end {pmatrix}, \quad \widehat {\boldsymbol {\beta }}= \begin {pmatrix} 0.353 \\ 0.474 \end {pmatrix}. \end{equation*}
\begin{equation*} \widehat {\mathbf {A}}= \begin {pmatrix} 0.578 & 0.178 \\ -1.221 & -0.169 \end {pmatrix}, \quad \widehat {\boldsymbol {\alpha }}= \begin {pmatrix} 7.105 \\ -1.579 \end {pmatrix}, \quad \widehat {\boldsymbol {\beta }}= \begin {pmatrix} 0.353 \\ 0.474 \end {pmatrix}. \end{equation*}
Now, we want to extract the rational component in order to find the optimal approximation. To do so, we block-diagonalize the transition matrix
![]() $\widehat{\mathbf{A}}$
and look at the modulus of its eigenvalues. We have:
$\widehat{\mathbf{A}}$
and look at the modulus of its eigenvalues. We have:
As we can see, both eigenvalues have modulus smaller than one. This means that the WFA
![]() $\widehat{A}$
is exactly the optimal approximation of size two that we are looking for, and there aren’t any components that need to be discarded. Following the notation introduced in the previous section, we have:
$\widehat{A}$
is exactly the optimal approximation of size two that we are looking for, and there aren’t any components that need to be discarded. Following the notation introduced in the previous section, we have:
![]() $\widehat{A}_k= \langle \widehat{\boldsymbol{\alpha }}_+, \widehat{\mathbf{A}}_+, \widehat{\boldsymbol{\beta }}_+ \rangle = \langle \widehat{\boldsymbol{\alpha }},\widehat{\mathbf{A}},\widehat{\boldsymbol{\beta }}\rangle$
.
$\widehat{A}_k= \langle \widehat{\boldsymbol{\alpha }}_+, \widehat{\mathbf{A}}_+, \widehat{\boldsymbol{\beta }}_+ \rangle = \langle \widehat{\boldsymbol{\alpha }},\widehat{\mathbf{A}},\widehat{\boldsymbol{\beta }}\rangle$
.
7. Related Work
The problem of minimizing automata has been an important subject of research since the 1950s. There is a remarkable algorithm due to Brzozowski (Brzozowski, Reference Brzozowski and Fox1962, Reference Brzozowski1964) that reduces a DFA to a minimal one. However, its worst-case running time is exponential in the number of states. Despite this shortcoming, this algorithm has seen a resurgence recently, mainly because it can be generalized to new models, such as weighted automata (Droste et al., Reference Droste, Kuich and Vogler2009). This line of algorithms is based on a new understanding of Brzozowski’s algorithm from the point of view of duality (Bonchi et al., Reference Bonchi, Bonsangue, Rutten, Silva, Constable and Silva2012b;Reference Bonchi, Bonsangue, Boreale, Rutten and Silvaa,Reference Bonchi, Bonsangue, Hansen, Panangaden, Rutten and Silva2014; Bezhanishvili et al., Reference Bezhanishvili, Kupke and Panangaden2012) and extends readily to other settings. In the context of quantitative systems, like weighted or probabilistic automata, it becomes meaningful to investigate different kinds of quantitative approximations and in particular of the approximate minimization problem. In Balle et al., (Reference Balle, Gourdeau, Panangaden, Chatzigiannakis, Indyk, Kuhn and Muscholl2017, Reference Balle, Gourdeau and Panangaden2022), the authors propose a bisimulation pseudometric to express the notion of behavioral proximity between states of WFAs. For example, this becomes particularly useful when a small perturbation has been applied to the parameters of the WFAs, and bisimulation alone would fail to capture their proximity. Similarly, in the context of finding a robust way of approximating dynamical systems despite the high sensitivity to the choice of parameters, Cardelli et al. (Reference Cardelli, Tribastone, Tschaikowski, Vandin, McIver and Horváth2018) introduce a notion of approximate bisimulation for ordinary differential equations with polynomial derivatives. Given a model and a parameter
![]() $\epsilon$
, they propose a method to compute an
$\epsilon$
, they propose a method to compute an
![]() $\epsilon$
bisimulation over the ODEs variables and then perturb minimally the model to obtain a new one where the
$\epsilon$
bisimulation over the ODEs variables and then perturb minimally the model to obtain a new one where the
![]() $\epsilon$
-bisimulation is an exact one. We remark that in this case the author generalizes the notion of differential equivalence that, while remaining very close to the concept of bisimulation defined for automata and dynamical systems, applies to ODE variables rather than the state space. The study of the approximate minimization problem and of its applications are fairly recent, and only a few works have been published on the subject. A problem analogous to approximate minimization is addressed by Kulesza, Jiang, and Singh for the spectral algorithm. The authors provide a bound on the loss of the learned low-rank model in terms of the singular values that are discarded during training (Kulesza et al., Reference Kulesza, Jiang and Singh2015). In a previous work, the same group of authors connected spectral learning to the approximation problem of a small class of Hidden Markov models, bounding the error in terms of the total variation distance (Kulesza et al., Reference Kulesza, Rao, Singh, Kaski and Corander2014). Still in the context of Hidden Markov models, Kotsalis and Shamma provide bounds for the model reduction problem using the spectral norm as a measure of the error (Kotsalis and Shamma, Reference Kotsalis and Shamma2015). We remark that the framework of Hidden Markov models is encompassed by weighted automata (Denis and Esposito, Reference Denis and Esposito2008). Balle, Panangaden, and Precup are the first authors to formalize the approximate minimization problem for WFAs (Balle et al., Reference Balle, Panangaden and Precup2015, Reference Balle, Panangaden and Precup2019). The technique presented in their paper relies on the construction (and truncation) of the singular value automaton, a canonical expression for WFAs arising from the singular value decomposition of the corresponding Hankel matrix. Their method can be viewed as a generalization to multi-letter alphabets of the balanced realization approach from control theory (Antoulas, Reference Antoulas2005). The authors conclude their analysis by providing bounds on the approximation error in the
$\epsilon$
-bisimulation is an exact one. We remark that in this case the author generalizes the notion of differential equivalence that, while remaining very close to the concept of bisimulation defined for automata and dynamical systems, applies to ODE variables rather than the state space. The study of the approximate minimization problem and of its applications are fairly recent, and only a few works have been published on the subject. A problem analogous to approximate minimization is addressed by Kulesza, Jiang, and Singh for the spectral algorithm. The authors provide a bound on the loss of the learned low-rank model in terms of the singular values that are discarded during training (Kulesza et al., Reference Kulesza, Jiang and Singh2015). In a previous work, the same group of authors connected spectral learning to the approximation problem of a small class of Hidden Markov models, bounding the error in terms of the total variation distance (Kulesza et al., Reference Kulesza, Rao, Singh, Kaski and Corander2014). Still in the context of Hidden Markov models, Kotsalis and Shamma provide bounds for the model reduction problem using the spectral norm as a measure of the error (Kotsalis and Shamma, Reference Kotsalis and Shamma2015). We remark that the framework of Hidden Markov models is encompassed by weighted automata (Denis and Esposito, Reference Denis and Esposito2008). Balle, Panangaden, and Precup are the first authors to formalize the approximate minimization problem for WFAs (Balle et al., Reference Balle, Panangaden and Precup2015, Reference Balle, Panangaden and Precup2019). The technique presented in their paper relies on the construction (and truncation) of the singular value automaton, a canonical expression for WFAs arising from the singular value decomposition of the corresponding Hankel matrix. Their method can be viewed as a generalization to multi-letter alphabets of the balanced realization approach from control theory (Antoulas, Reference Antoulas2005). The authors conclude their analysis by providing bounds on the approximation error in the
![]() $\ell ^2$
norm. The result is supported by strong theoretical guarantees and applies to a large class of WFAs. This method has later been extended to the setting of weighted tree automata in Balle and Rabusseau (Reference Balle and Rabusseau2020). The main limitation of these approaches based on SVA truncation is that the approximation obtained is not optimal in any norm. We partially address this point in this work, where we obtain an algorithm for the optimal approximation in the spectral norm for the same class of WFAs considered by Balle, Panangaden, and Precup, but restricted to a one-letter alphabet. Part of this results were presented in (Balle et al., Reference Balle, Lacroce, Panangaden, Precup, Rabusseau, Bansal, Merelli and Worrell2021). In Lacroce et al. (Reference Lacroce, Panangaden, Rabusseau, Chandlee, Eyraud, Heinz, Jardine and van Zaanen2021), we extend this results to the more general setting of black-box models trained for language modeling over one-letter alphabets. In Lacroce et al. (Reference Lacroce, Panangaden and Rabusseau2022); Lacroce (Reference Lacroce2022), we analyze the problem of extending the method presented in this paper to the case of multi-letter alphabets.
$\ell ^2$
norm. The result is supported by strong theoretical guarantees and applies to a large class of WFAs. This method has later been extended to the setting of weighted tree automata in Balle and Rabusseau (Reference Balle and Rabusseau2020). The main limitation of these approaches based on SVA truncation is that the approximation obtained is not optimal in any norm. We partially address this point in this work, where we obtain an algorithm for the optimal approximation in the spectral norm for the same class of WFAs considered by Balle, Panangaden, and Precup, but restricted to a one-letter alphabet. Part of this results were presented in (Balle et al., Reference Balle, Lacroce, Panangaden, Precup, Rabusseau, Bansal, Merelli and Worrell2021). In Lacroce et al. (Reference Lacroce, Panangaden, Rabusseau, Chandlee, Eyraud, Heinz, Jardine and van Zaanen2021), we extend this results to the more general setting of black-box models trained for language modeling over one-letter alphabets. In Lacroce et al. (Reference Lacroce, Panangaden and Rabusseau2022); Lacroce (Reference Lacroce2022), we analyze the problem of extending the method presented in this paper to the case of multi-letter alphabets.
The control theory community has largely studied approximate minimization in the context of linear time-invariant systems (Antoulas, Reference Antoulas2005). A parallel with these results can be drawn by noting that the impulse response of a discrete Single-Input-Single-Output SISO system can be parametrized as a WFA over a one-letter alphabet. Glover (Reference Glover1984) presents a state-space solution for the case of continuous Multi-Input-Multi-Output MIMO systems. His method led to a widespread application of these results, thanks to its computational and theoretical simplicity. This stems from the structure of the continuous Lyapunov equations. For discrete systems, though, the quadratic nature of the Lyapunov equations does not allow for a simple closed-form formula for the state-space solution (Chui and Chen, Reference Chui and Chen1997). Thus, most of the results for the discrete case work with a suboptimal version of the problem (Ball and Ran, Reference Ball and Ran1987; Al-Hussari et al., Reference Al-Hussari, Jaimoukha and Limebeer1993; Ionescu and Oara, Reference Ionescu and Oara2001). A solution for the SISO case can be found using a polynomial approach, but it does not provide an explicit representation of the state space nor it generalizes to the MIMO setting. The first to actually extend Glover results is Gu, who provides an elegant solution for the MIMO discrete problem (Gu, 2005). Glover and Gu’s solutions rely on building an all-pass system, equivalent to the WFA
![]() $E$
in our case. Part of our contribution is the adaptation of some of the control theory tools to WFAs.
$E$
in our case. Part of our contribution is the adaptation of some of the control theory tools to WFAs.
8. Extensions and Future Work
In this section, we examine possible extensions of our method by relaxing some of the hypothesis.
8.1 Removing the finite-rank assumption
The proof of Theorem 12 is constructive for any compact Hankel operator. In the setting of this paper, compactness is guaranteed, as the operator corresponding to an irredundant WFA has finite rank and is bounded. While boundness is necessary for compactness, the finite-rank hypothesis is not. Therefore, an interesting extension of this work is to investigate other classes of models by relaxing the finite-rank (or finite state) assumption. An example of models corresponding to infinite-rank Hankel matrices is recurrent neural networks (RNNs) (Hochreiter and Schmidhuber, Reference Hochreiter and Schmidhuber1997). Recently, particular attention has been given to the problem of extracting, from an RNN, a weighted finite automaton (Ayache et al., Reference Ayache, Eyraud and Goudian2018; Rabusseau et al., Reference Rabusseau, Li, Precup, Chaudhuri and Sugiyama2019; Weiss et al., Reference Weiss, Goldberg and Yahav2019; Theertha Suresh et al., Reference Theertha Suresh, Roark, Riley and Schogol2021; Okudono et al., Reference Okudono, Waga, Sekiyama and Hasuo2020; Eyraud and Ayache Reference Eyraud and Ayache2024; Zhang et al., Reference Zhang, Du, Xie, Ma, Liu and Sun2021). In this sense, the knowledge distillation task (Hinton et al., Reference Hinton, Vinyals and Dean2015) is very similar to an approximate minimization problem, since WFAs are a less expensive alternative to RNNs, while still being expressive and suited for sequence modeling and prediction (Cortes et al., Reference Cortes, Haffner and Mohri2004; Denis and Esposito, Reference Denis and Esposito2008). In Lacroce et al. (Reference Lacroce, Panangaden, Rabusseau, Chandlee, Eyraud, Heinz, Jardine and van Zaanen2021), we investigated the use of AAK theory on black-box models trained for language modeling on sequential data. In particular, we showed that compactness is automatically respected by black boxes for language modeling, and proposed an algorithm for the one-letter setting, based on AAK theory. This particular extension of the method presented in this paper constitutes a first fundamental step towards developing provable approximation algorithms for black-box models.
8.2 Removing the spectral radius assumption
One could consider a WFA over a one-letter alphabet with
![]() $\rho (\mathbf{A})\neq 1$
, that is not necessarily irredundant. In this case, the method proposed in the previous sections can be extended and the quality of the approximation can be estimated, but the result is not optimal in the spectral norm. Once again, we draw inspiration from the control theory literature, where some theoretical work has been done to study an analogous approach for continuous time systems and their approximation error (Glover, Reference Glover1984).
$\rho (\mathbf{A})\neq 1$
, that is not necessarily irredundant. In this case, the method proposed in the previous sections can be extended and the quality of the approximation can be estimated, but the result is not optimal in the spectral norm. Once again, we draw inspiration from the control theory literature, where some theoretical work has been done to study an analogous approach for continuous time systems and their approximation error (Glover, Reference Glover1984).
The key idea is to block-diagonalize
![]() $\mathbf{A}$
like we did in Section 4.3.3. This way, we obtain two components,
$\mathbf{A}$
like we did in Section 4.3.3. This way, we obtain two components,
![]() $\mathbf{A}_+$
and
$\mathbf{A}_+$
and
![]() $\mathbf{A}_-$
, with the property that
$\mathbf{A}_-$
, with the property that
![]() $\rho \lt 1$
and
$\rho \lt 1$
and
![]() $\rho \gt 1$
, respectively. We tackle each component separately. The case of
$\rho \gt 1$
, respectively. We tackle each component separately. The case of
![]() $A_+=\langle \boldsymbol{\alpha }_+, \mathbf{A}_+, \boldsymbol{\beta }_+ \rangle$
, the component having
$A_+=\langle \boldsymbol{\alpha }_+, \mathbf{A}_+, \boldsymbol{\beta }_+ \rangle$
, the component having
![]() $\rho (\mathbf{A})\lt 1$
, can be dealt with in the way presented in the previous sections. This means that we can find an optimal spectral-norm approximation of the desired size for
$\rho (\mathbf{A})\lt 1$
, can be dealt with in the way presented in the previous sections. This means that we can find an optimal spectral-norm approximation of the desired size for
![]() $A_+$
. Then, we can consider the second component,
$A_+$
. Then, we can consider the second component,
![]() $A_-=\langle \boldsymbol{\alpha }_-, \mathbf{A}_-, \boldsymbol{\beta }_- \rangle$
. In this case, we apply the transformation
$A_-=\langle \boldsymbol{\alpha }_-, \mathbf{A}_-, \boldsymbol{\beta }_- \rangle$
. In this case, we apply the transformation
to the symbol
![]() $\phi ^{\prime}(z)$
associated to
$\phi ^{\prime}(z)$
associated to
![]() $A_-$
. Then, the function
$A_-$
. Then, the function
is well defined, as the series converges for
![]() $z$
with small enough modulus. The use of this transformation allows us to obtain a function having poles only inside the unit disc, and to apply the method presented in this chapter. We remark that in this case, an important choice to make is the size of the target approximation of
$z$
with small enough modulus. The use of this transformation allows us to obtain a function having poles only inside the unit disc, and to apply the method presented in this chapter. We remark that in this case, an important choice to make is the size of the target approximation of
![]() $A_-$
, as it can influence the quality of the result. Analyzing the effects of this parameter on the approximation error is an interesting direction for future work, both on the theoretical and experimental side.
$A_-$
, as it can influence the quality of the result. Analyzing the effects of this parameter on the approximation error is an interesting direction for future work, both on the theoretical and experimental side.
8.3 Removing the one-letter assumption
The most pressing direction for future work is undoubtedly to extend our results to a multi-letter setting. The work of Adamyan, Arov and Krein provides us with a powerful theory connecting sequences to the study of complex functions. Unfortunately, this approach cannot be directly generalized to the multi-letter case, when
![]() $\Sigma ^*$
is a noncommutative monoid, as it requires to generalize standard harmonic analysis results to the non-abelian case. A recent line of work in multivariable operator theory has been centered around extending results of standard operator theory to the case of noncommutative operators defined on Fock spaces Frazho (Reference Frazho1982); Bunce (Reference Bunce1984); Arias and Popescu (Reference Arias and Popescu1995); Popescu (Reference Popescu1989, Reference Popescu1992, Reference Popescu1993, Reference Popescu1995, Reference Popescu2003, Reference Popescu2006, Reference Popescu2010, Reference Popescu2013); Ball and Bolotnikov (Reference Ball and Bolotnikov2021); Jury et al. (Reference Jury, Martin and Shamovich2021). In particular, a noncommutative definition of Hankel operator, and a noncommutative version of the AAK theorem are presented in a recent work of Popescu Popescu (Reference Popescu2003), but its proof is not constructive. Therefore, solving the approximate minimization problem for multi-letter alphabets using AAK theory comes with two distinct challenges:
$\Sigma ^*$
is a noncommutative monoid, as it requires to generalize standard harmonic analysis results to the non-abelian case. A recent line of work in multivariable operator theory has been centered around extending results of standard operator theory to the case of noncommutative operators defined on Fock spaces Frazho (Reference Frazho1982); Bunce (Reference Bunce1984); Arias and Popescu (Reference Arias and Popescu1995); Popescu (Reference Popescu1989, Reference Popescu1992, Reference Popescu1993, Reference Popescu1995, Reference Popescu2003, Reference Popescu2006, Reference Popescu2010, Reference Popescu2013); Ball and Bolotnikov (Reference Ball and Bolotnikov2021); Jury et al. (Reference Jury, Martin and Shamovich2021). In particular, a noncommutative definition of Hankel operator, and a noncommutative version of the AAK theorem are presented in a recent work of Popescu Popescu (Reference Popescu2003), but its proof is not constructive. Therefore, solving the approximate minimization problem for multi-letter alphabets using AAK theory comes with two distinct challenges:
-
• Finding a noncommutative Hankel operator: given a WFA and its Hankel matrix, we need to find a way to reformulate the approximation problem using multivariable operators. In particular, we need to find a noncommutative analogue of the Hardy space and of the symbol.
-
• Making AAK constructive: the proof of the noncommutative version of the AAK theorem does not provide us with an expression for the optimal approximation. An interesting direction would be to explore ways to extend the proof to a constructive one.
In Lacroce et al. (Reference Lacroce, Panangaden and Rabusseau2022), we proposed a framework to associate a noncommutative Hankel operator (defined on a noncommutative version of the Hardy space) and a noncommutative rational function to the Hankel matrix computed by a model on sequential data, solving the first point listed above. In the one-letter case, obtaining the framework allowed us to reformulate the approximation problem in terms of functional analysis, and to solve it using the constructive proof of AAK theorem. In Lacroce (Reference Lacroce2022), we tried to address the question of whether or not the proof of the noncommutative AAK theorem can be made constructive. While we did not manage to provide a definitive answer, we laid out possible approaches that can be used to tackle the problem of making the proof of the noncommutative version of AAK theorem constructive.
9. Conclusion
In this paper, we applied the AAK theory for Hankel operators and complex functions with the framework of WFAs in order to construct the optimal approximation to an automaton given a bound on the size. We propose an algorithm to find the parameters of the best WFA approximation in the spectral norm and derive bounds on the error. Our method applies to real irredundant WFAs defined over a one-letter alphabet. These alphabets have proven to be of independent interest when dealing with automata, as in this case the classes of regular and context-free languages collapse (Pighizzini, Reference Pighizzini2015).
We think the spectral norm has desirable characteristics, making it a solid candidate for the approximate minimization task. For example, it can be minimized in polynomial time and a global minimum for the error can be computed accurately. Moreover, the fact that this norm is independent on the specific architecture or model considered facilitates future applications of this method, as it can be used to compare different classes of models. Nonetheless, a limitation of this work is that we do not have a clear picture of how effective it is to use the spectral norm to evaluate the approximation of WFAs and black boxes. Concretely, we do not know how the spectral norm performs with respect to behavioral metrics, or other metrics coming from natural language processing (e.g., word error rate and normalized discounted cumulative gain). To some extent, this problem is a collateral effect of the size of the alphabet: the comparison between spectral norm and other kind of norms is possible only in the multi-letter setting. Obtaining algorithms for the multi-letter case will thus open the possibility of evaluating the quality of the spectral norm.
While the one-letter setting is certainly restricted, we believe that this work constitutes a first fundamental step in the direction of optimal approximation. Furthermore, the use of AAK techniques has proven to be very fruitful in related areas like control theory; we think that automata theory can also benefit from it. The use of such methods can help deepen the understanding of the behavior of rational functions. This paper highlights and strengthens the interesting connections between functional analysis, automata theory, and control theory, unifying tools from different domains in one formalism.
Acknowledgments
This research has been supported by NSERC Canada (C. Lacroce, P. Panangaden) and Canada CIFAR AI chairs program (G. Rabusseau). The authors would like to thank Doina Precup, Tianyu Li, Harsh Satija, and Alessandro Sordoni for feedback on earlier drafts of this work, Gheorghe Comanici and Robert Robere for a detailed review, Florence Clerc for help with the submission, and Maxime Wabartha for fruitful discussions and comments on proofs.
Competing interests
The authors declare none.