Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Master, Jade
2020.
Petri nets based on Lawvere theories.
Mathematical Structures in Computer Science,
Vol. 30,
Issue. 7,
p.
833.
Kachi, Fatma
Bouanaka, Chafia
and
Merkouche, Souheir
2020.
A Formal Model for Quality-Driven Decision Making in Self-Adaptive Systems.
Electronic Proceedings in Theoretical Computer Science,
Vol. 329,
Issue. ,
p.
48.
Baez, John C.
Genovese, Fabrizio
Master, Jade
and
Shulman, Michael
2021.
Categories of Nets.
p.
1.
Watanabe, Kazuki
Eberhart, Clovis
Asada, Kazuyuki
and
Hasuo, Ichiro
2021.
A Compositional Approach to Parity Games.
Electronic Proceedings in Theoretical Computer Science,
Vol. 351,
Issue. ,
p.
278.
Foley, John D.
Breiner, Spencer
Subrahmanian, Eswaran
and
Dusel, John M.
2021.
Operads for complex system design specification, analysis and synthesis.
Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 477,
Issue. 2250,
Genovese, Fabrizio Romano
Herold, Jelle
Loregian, Fosco
and
Palombi, Daniele
2021.
A Categorical Semantics for Hierarchical Petri Nets.
Electronic Proceedings in Theoretical Computer Science,
Vol. 350,
Issue. ,
p.
51.
Waites, W.
Cavaliere, M.
Manheim, D.
Panovska-Griffiths, J.
and
Danos, V.
2021.
Rule-based epidemic models.
Journal of Theoretical Biology,
Vol. 530,
Issue. ,
p.
110851.
Libkind, Sophie
Baas, Andrew
Halter, Micah
Patterson, Evan
and
Fairbanks, James P.
2022.
An algebraic framework for structured epidemic modelling.
Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 380,
Issue. 2233,
Breiner, S.
Subrahmanian, E.
and
Sriram, R. D.
2022.
Handbook of Model-Based Systems Engineering.
p.
1.
Bakirtzis, Georgios
Genovese, Fabrizio
and
Fleming, Cody H.
2022.
Yoneda Hacking: The Algebra of Attacker Actions.
ACM Transactions on Cyber-Physical Systems,
Vol. 6,
Issue. 3,
p.
1.
Karr, Jonathan
Malik-Sheriff, Rahuman S.
Osborne, James
Gonzalez-Parra, Gilberto
Forgoston, Eric
Bowness, Ruth
Liu, Yaling
Thompson, Robin
Garira, Winston
Barhak, Jacob
Rice, John
Torres, Marcella
Dobrovolny, Hana M.
Tang, Tingting
Waites, William
Glazier, James A.
Faeder, James R.
and
Kulesza, Alexander
2022.
Model Integration in Computational Biology: The Role of Reproducibility, Credibility and Utility.
Frontiers in Systems Biology,
Vol. 2,
Issue. ,
Baez, John C.
Courser, Kenny
and
Vasilakopoulou, Christina
2022.
Structured versus Decorated Cospans.
Compositionality,
Vol. 4,
Issue. ,
p.
3.
Waites, W.
Cavaliere, M.
Danos, V.
Datta, R.
Eggo, R. M.
Hallett, T. B.
Manheim, D.
Panovska-Griffiths, J.
Russell, T. W.
and
Zarnitsyna, V. I.
2022.
Compositional modelling of immune response and virus transmission dynamics.
Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 380,
Issue. 2233,
Kock, Joachim
2023.
Whole-grain Petri Nets and Processes.
Journal of the ACM,
Vol. 70,
Issue. 1,
p.
1.
Kachi, Fatma
and
Bouanaka, Chafia
2023.
A hybrid model for efficient decision-making in self-adaptive systems.
Information and Software Technology,
Vol. 153,
Issue. ,
p.
107063.
Breiner, S.
Subrahmanian, E.
and
Sriram, R. D.
2023.
Handbook of Model-Based Systems Engineering.
p.
1259.
Castellan, Simon
and
Clairambault, Pierre
2023.
The Geometry of Causality: Multi-token Geometry of Interaction and Its Causal Unfolding.
Proceedings of the ACM on Programming Languages,
Vol. 7,
Issue. POPL,
p.
689.
Gogioso, Stefano
Wang-Maścianica, Vincent
Waseem, Muhammad Hamza
Scandolo, Carlo Maria
and
Coecke, Bob
2023.
Constructor Theory as Process Theory.
Electronic Proceedings in Theoretical Computer Science,
Vol. 397,
Issue. ,
p.
137.
Ritter, Daniel
Nordvall Forsberg, Fredrik
and
Rinderle-Ma, Stefanie
2024.
Responsible composition and optimization of integration processes under correctness preserving guarantees.
Information Systems,
Vol. 124,
Issue. ,
p.
102400.
Díaz-Marín, Homero G.
and
Sánchez-Ponce, José L.
2024.
Intraspecific and monotone enzyme catalysis with oscillatory substrate and inhibitor supplies.
Journal of Mathematical Chemistry,
Vol. 62,
Issue. 9,
p.
2160.
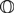 ${\mathbb O}$pen(Petri). We describe two forms of semantics for open Petri nets using symmetric monoidal double functors out of
${\mathbb O}$pen(Petri). We describe two forms of semantics for open Petri nets using symmetric monoidal double functors out of 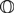 ${\mathbb O}$pen(Petri). The first, an operational semantics, gives for each open Petri net a category whose morphisms are the processes that this net can carry out. This is done in a compositional way, so that these categories can be computed on smaller subnets and then glued together. The second, a reachability semantics, simply says which markings of the outputs can be reached from a given marking of the inputs.
${\mathbb O}$pen(Petri). The first, an operational semantics, gives for each open Petri net a category whose morphisms are the processes that this net can carry out. This is done in a compositional way, so that these categories can be computed on smaller subnets and then glued together. The second, a reachability semantics, simply says which markings of the outputs can be reached from a given marking of the inputs.