Article contents
Separating minimal valuations, point-continuous valuations, and continuous valuations
Published online by Cambridge University Press: 07 December 2021
Abstract
We give two concrete examples of continuous valuations on dcpo’s to separate minimal valuations, point-continuous valuations, and continuous valuations:
(1) Let
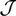 ${\mathcal J}$ be the Johnstone’s non-sober dcpo, and μ be the continuous valuation on
${\mathcal J}$ be the Johnstone’s non-sober dcpo, and μ be the continuous valuation on 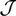 ${\mathcal J}$ with μ(U)=1 for nonempty Scott opens U and μ(U)=0 for
${\mathcal J}$ with μ(U)=1 for nonempty Scott opens U and μ(U)=0 for 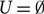 $U=\emptyset$. Then, μ is a point-continuous valuation on
$U=\emptyset$. Then, μ is a point-continuous valuation on 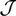 ${\mathcal J}$ that is not minimal.
${\mathcal J}$ that is not minimal.(2) Lebesgue measure extends to a measure on the Sorgenfrey line
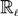 $\mathbb{R}_\ell$. Its restriction to the open subsets of
$\mathbb{R}_\ell$. Its restriction to the open subsets of 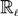 $\mathbb{R}_\ell$ is a continuous valuation λ. Then, its image valuation
$\mathbb{R}_\ell$ is a continuous valuation λ. Then, its image valuation 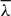 $\overline\lambda$ through the embedding of
$\overline\lambda$ through the embedding of 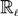 $\mathbb{R}_\ell$ into its Smyth powerdomain
$\mathbb{R}_\ell$ into its Smyth powerdomain 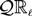 $\mathcal{Q}\mathbb{R}_\ell$ in the Scott topology is a continuous valuation that is not point-continuous.
$\mathcal{Q}\mathbb{R}_\ell$ in the Scott topology is a continuous valuation that is not point-continuous.
We believe that our construction 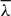 $\overline\lambda$ might be useful in giving counterexamples displaying the failure of the general Fubini-type equations on dcpo’s.
$\overline\lambda$ might be useful in giving counterexamples displaying the failure of the general Fubini-type equations on dcpo’s.
Information
- Type
- Paper
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
- 2
- Cited by


