Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Eskin, Gregory
1976.
A parametrix for mixed problems for strictly hyberbolic equations of arbitrary order.
Communications in Partial Differential Equations,
Vol. 1,
Issue. 6,
p.
521.
Duff, G. F. D.
1977.
Boundary Value Problems for Linear Evolution Partial Differential Equations.
p.
27.
Eskin, Gregory
1977.
Parametrix and propagation of singularities for the interior mixed hyperbolic problem.
Journal d'Analyse Mathématique,
Vol. 32,
Issue. 1,
p.
17.
Andersson, K. G.
and
Melrose, R. B.
1977.
The propagation of singularities along gliding rays.
Inventiones Mathematicae,
Vol. 41,
Issue. 3,
p.
197.
Friedlander, F. G.
and
Melrose, R. B.
1977.
The wave front set of the solution of a simple initial-boundary value problem with glancing rays. II.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 81,
Issue. 1,
p.
97.
Melrose, R. B.
1978.
Airy operators.
Communications in Partial Differential Equations,
Vol. 3,
Issue. 1,
p.
1.
Taylor, Michael E.
1978.
Propagation, reflection, and diffraction of singularities of solutions to wave equations.
Bulletin of the American Mathematical Society,
Vol. 84,
Issue. 4,
p.
589.
Alinhac, Serge
1978.
Solution explicite du probleme de Cauchy pour des operateurs
effectivement hyperboliques.
Duke Mathematical Journal,
Vol. 45,
Issue. 2,
Helffer, Bernard
1980.
Séminaire Bourbaki vol. 1978/79 Exposés 525 – 542.
Vol. 770,
Issue. ,
p.
1.
Eskin, Gregory
1981.
Singularities in Boundary Value Problems.
p.
19.
Lascar, Richard
1981.
Propagation des Singularités des Solutions d’Equations Pseudo-Différentielles à Caractéristiques de Multiplicités Variables.
Vol. 856,
Issue. ,
p.
106.
Gramtcheff, Todor V.
1981.
An application of airy functions to the Tricomi problem.
Mathematische Nachrichten,
Vol. 102,
Issue. 1,
p.
169.
Melrose, Richard B.
1981.
Singularities in Boundary Value Problems.
p.
133.
Eskin, Gregory
1981.
Initial boundary value problem for second order hyperbolic equations with general boundary conditions I.
Journal d'Analyse Mathématique,
Vol. 40,
Issue. 1,
p.
43.
Beals, Michael
1982.
Local Lp estimates for fourier‐airy integral operators.
Communications on Pure and Applied Mathematics,
Vol. 35,
Issue. 6,
p.
751.
Williams, Mark
1983.
Wa vefront sets of extensions of solutions to diffractive boundary problems..
Communications in Partial Differential Equations,
Vol. 8,
Issue. 8,
p.
1.
Mizohata, S.
Ohya, Y.
and
Ikawa, M.
1986.
Hyperbolic Equations and Related Topics.
p.
ix.
Fontong, Wu
1988.
Partial Differential Equations.
Vol. 1306,
Issue. ,
p.
224.
Egorov, Yu. V.
and
Shubin, M. A.
1994.
Partial Differential Equations II.
Vol. 31,
Issue. ,
p.
1.
Smith, Hart F.
and
Sogge, Christopher D.
1994.
Lp regularity for the wave equation with strictly
convex obstacles.
Duke Mathematical Journal,
Vol. 73,
Issue. 1,
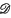 ′ (Ω) and Pu = 0, the wave front set of u, WF(u), is a set in the cotangent bundle T*Ω (minus the zero section) that is contained in p−1(0) and is invariant under the flow generated in p−1(0) by the Hamiltonian vector field (gradξp, − gradxp). In other words, WF(u) is made up of bicharacteristic strips. This is a special case of an important theorem due to Hörmander (5), and Duistermaat and Hörmander (1), which generalizes classical results on the relation between discontinuities of solutions of a partial differential equation and the characteristics of the equation.
′ (Ω) and Pu = 0, the wave front set of u, WF(u), is a set in the cotangent bundle T*Ω (minus the zero section) that is contained in p−1(0) and is invariant under the flow generated in p−1(0) by the Hamiltonian vector field (gradξp, − gradxp). In other words, WF(u) is made up of bicharacteristic strips. This is a special case of an important theorem due to Hörmander (5), and Duistermaat and Hörmander (1), which generalizes classical results on the relation between discontinuities of solutions of a partial differential equation and the characteristics of the equation.
