Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Künzi, H.-P. A.
1986.
TOPOLOGICAL SPACES WITH A COARSEST COMPATIBLE QUASI-PROXIMITY.
Quaestiones Mathematicae,
Vol. 10,
Issue. 2,
p.
179.
Künzi, Hans-Peter A.
1989.
Some remarks on quasi-uniform spaces.
Glasgow Mathematical Journal,
Vol. 31,
Issue. 3,
p.
309.
Künzi, Hans-Peter A.
and
Ferrario, Nathalie
1991.
Bicompleteness of the fine quasi-uniformity.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 109,
Issue. 1,
p.
167.
KÜNZI, HANS‐PETER A.
1992.
Quasi Uniformities Defined by Sets of Neighborhoodsa.
Annals of the New York Academy of Sciences,
Vol. 659,
Issue. 1,
p.
125.
Schauerte, A.
1993.
On the MacNeille Completion of the Category of Partially Ordered Topological Spaces.
Mathematische Nachrichten,
Vol. 163,
Issue. 1,
p.
281.
Ivanov, A. A.
1996.
Bibliography on bitopological spaces. 2.
Journal of Mathematical Sciences,
Vol. 81,
Issue. 2,
p.
2497.
Künzi, Hans-Peter A.
and
Watson, Stephen
1996.
A nontrivial T1-space admitting a unique quasi-proximity.
Glasgow Mathematical Journal,
Vol. 38,
Issue. 2,
p.
207.
PIN, J.-E.
and
WEIL, P.
1999.
UNIFORMITIES ON FREE SEMIGROUPS.
International Journal of Algebra and Computation,
Vol. 09,
Issue. 03n04,
p.
431.
Künzi, H.-P. A.
and
Pérez-Peñalver, M. J.
2000.
The Number of Compatible Totally Bounded Quasi-Uniformities.
Acta Mathematica Hungarica,
Vol. 88,
Issue. 1-2,
p.
15.
Salbany, S.
and
Romaguera, S.
2000.
DIEUDONN ÉCOMPLETE BISPACES.
Studia Scientiarum Mathematicarum Hungarica,
Vol. 36,
Issue. 3-4,
p.
407.
Nailana, K. R.
2000.
Papers in Honour of Bernhard Banaschewski.
p.
445.
Sünderhauf, Philipp
2000.
Sobriety in Terms of Nets.
Applied Categorical Structures,
Vol. 8,
Issue. 4,
p.
649.
Erné, Marcel
2001.
Ideal Completions and Compactifications.
Applied Categorical Structures,
Vol. 9,
Issue. 3,
p.
217.
Jung, Achim
Kegelmann, Mathias
and
Moshier, M.Andrew
2001.
Stably Compact Spaces and Closed Relations.
Electronic Notes in Theoretical Computer Science,
Vol. 45,
Issue. ,
p.
209.
Künzi, H. P. A.
Romaguera, S.
and
Salbany, S.
2001.
Bispaces admitting only bicomplete or only totally bounded quasi-metrics.
Rendiconti del Circolo Matematico di Palermo,
Vol. 50,
Issue. 1,
p.
186.
Romaguera, Salvador
2001.
ALMOST 2-FULLY NORMAL, PAIRWISE PARACOMPACT AND COMPLETE DEVELOPABLE BISPACES.
Quaestiones Mathematicae,
Vol. 24,
Issue. 1,
p.
21.
Rodríguez-López, Jesús
and
Romaguera, Salvador
2002.
The relationship between the Vietoris topology and the Hausdorff quasi-uniformity.
Topology and its Applications,
Vol. 124,
Issue. 3,
p.
451.
Künzi, H.-P. A.
2002.
Quasi-Metrizable Spaces Satisfying Certain Completeness Conditions.
Acta Mathematica Hungarica,
Vol. 95,
Issue. 4,
p.
345.
2005.
Bitopological Spaces: Theory, Relations with Generalized Algebraic Structures, and Applications.
Vol. 199,
Issue. ,
p.
385.
Gerlo, A.
2008.
Approach Theory in a Category: A Study of Compactness and Hausdorff Separation.
Applied Categorical Structures,
Vol. 16,
Issue. 4,
p.
479.

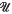 is a compatible totally bounded quasi-uniformity on a
is a compatible totally bounded quasi-uniformity on a 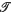 ), then the bicompletion
), then the bicompletion 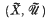 of (
of ( if and only if (
if and only if (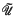 is the Pervin quasi-uniformity on
is the Pervin quasi-uniformity on 