No CrossRef data available.
Article contents
A Principle in classical mechanics with a ‘relativistic’ path-element extending the principle of least action
Published online by Cambridge University Press: 24 October 2008
Extract
1. A particle with mass m and coordinates x1 x2, x3 relative to a set of rectangular axes fixed in Newtonian space is moving in a field of conservative forces with a potential energy V(x1, x2, x3) and a kinetic energy
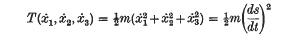
The equations of motion, written
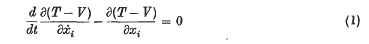
(representing the three equations i = l, i = 2, i = 3 in a way to be used in this paper), constitute, as they stand, a sufficient condition in order to ensure
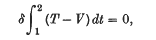
in the sense that the Hamiltonian integral has a stationary value if the actual motion is compared with neighbouring motions with the same terminal positions and the same terminal values of the time as in the actual motion.
Information
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 51 , Issue 3 , July 1955 , pp. 469 - 475
- Copyright
- Copyright © Cambridge Philosophical Society 1955

