Hostname: page-component-745bb68f8f-mzp66 Total loading time: 0 Render date: 2025-01-26T22:50:06.356Z Has data issue: false hasContentIssue false
  • English
  • Français

On the integral Hodge conjecture for varieties with trivial Chow group

Published online by Cambridge University Press:  17 May 2023

HUMBERTO A. DIAZ
HUMBERTO A. DIAZ*
Affiliation:
Washington University in Saint Louis, 1 Brookings Dr., St. Louis, MO 63130, U.S.A. e-mail: humbertoadiaziii@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

We obtain examples of smooth projective varieties over 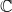${\mathbb C}$ that violate the integral Hodge conjecture and for which the total Chow group is of finite rank. Moreover, we show that there exist such examples defined over number fields.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 175 , Issue 2 , September 2023 , pp. 433 - 443
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Cambridge Philosophical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Atiyah, M. F. and Hirzebruch, F.. Analytic cycles on complex manifolds. Topology 1 (1962), 25–45.CrossRefGoogle Scholar
Benoist, O. and Ottem, J. C.. Failure of the integral Hodge conjecture for threefolds of Kodaira dimension zero. Comment. Math. Helv. 95 (2020), 27–35.CrossRefGoogle Scholar
Bloch, S.. Torsion algebraic cycles and a theorem of Roitman. Comp. Math. 39(1) (1979), 107–127.Google Scholar
Bloch, S., Kas, A. and Lieberman, D.. Zero cycles on surfaces with $p_{g}=0$ . Comp. Math. 33(2) (1976), 135–145.Google Scholar
Bloch, S. and Ogus, A.. Gersten’s conjecture and the homology of schemes. Ann. Sci. Ecole Norm. Sup, (4). 7(2) (1974), 181–201.CrossRefGoogle Scholar
Colliot–Thélène, J.–L.. Cohomologie non ramifiée dans le produit avec une courbe elliptique. Manuscripta Math. 160(2019), 561–565.CrossRefGoogle Scholar
Colliot–Thélène, J.–L. and Ojanguren, M.. Variétés unirationnelles non rationnelles: au-delà de l’exemple d’Artin et Mumford. Invent. Math. 97(1) (1989), 141–158.CrossRefGoogle Scholar
Colliot-Thélène, J.–L. and Voisin, C.. Cohomologie non ramifiée et conjecture de Hodge entiére. Duke Math. J. 161(5) (2012), 735–801.CrossRefGoogle Scholar
Gabber, O.. Appendix to Exposant et indice d’algèbres simples centrales non ramifiées, By J.–L. Colliot–Thélène. Enseign. Math. 48(1)-(2) (2002), 127–146.Google Scholar
Guletskii, V. and Pedrini, C.. The Chow motive of the Godeaux surface. Proceedings of the Conference on Algebraic Geometry in memory of P. Francia, (W. De Gruyter, Berlin-New York 2002), 179–196.CrossRefGoogle Scholar
Hulek, K. and Schütt, M.. Enriques surfaces and Jacobian elliptic K3 surfaces. Math. Zeit. 268 (2011), 1025–1056.CrossRefGoogle Scholar
Kollár, J.. Classification of irregular varieties, ed. E. Ballico, F. Catanese and C. Ciliberto. Lecture Notes in Math. 1515 (Springer, 1990).Google Scholar
Milne, J.. Étale Cohomology. (Princeton University Press, 1980).Google Scholar
Mumford, D.. Rational equivalence of zero cycles on surfaces. J. Math. Kyoto 9 (1969), 195–204.Google Scholar
Ottem, J. C. and Suzuki, F.. A pencil of Enriques surfaces with non-algebraic integral Hodge classes. To appear in Math. Ann. Google Scholar
Patel, D. and Ravindra, G. V.. Lefschetz theorems for torsion algebraic cycles in codimension 2. Adv. Math. 315 (2017), 554–575.Google Scholar
Pedrini, C. and Weibel, C.. Some surfaces of general type for which Bloch’s conjecture holds. Period Domains, Algebraic Cycles and Arithmetic (Cambridge University Press, 2016).CrossRefGoogle Scholar
Schreieder, S.. Refined unramified homology of schemes. Preprint 2021, arXiv:2010.05814v4.Google Scholar
Soulé, C. and Voisin, C.. Torsion cohomology classes and algebraic cycles on complex manifolds. Adv. Math. 198 (2005), 107–127.CrossRefGoogle Scholar
Totaro, B.. On the integral Hodge and Tate conjectures over a number field. Forum Math. Sigma 1 (2013), e4 (13 pages).CrossRefGoogle Scholar
Vial, C.. Projectors on the intermediate algebraic Jacobians. New York J. Math. 19 (2013), 793–822.Google Scholar
Voisin, C.. Bloch’s conjecture for Catanese and Barlow surfaces. J. Differential Geom. 97 (2014), 149–175.CrossRefGoogle Scholar