Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Acrivos, Andreas
1956.
The Transient Response of Stagewise Processes.
Journal of the Society for Industrial and Applied Mathematics,
Vol. 4,
Issue. 2,
p.
120.
Luke, Yudell L.
1956.
Evaluation of an integral arising in numerical integration near a logarithmic singularity.
Mathematics of Computation,
Vol. 10,
Issue. 53,
p.
14.
Acrivos, Andreas
1956.
The Transient Response of Stagewise Processes.
Journal of the Society for Industrial and Applied Mathematics,
Vol. 4,
Issue. 1,
p.
1.
Longman, I. M.
1956.
Note on a method for computing infinite integrals of oscillatory functions.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 52,
Issue. 4,
p.
764.
Hurwitz, H.
and
Zweifel, P. F.
1956.
Numerical quadrature of Fourier transform integrals.
Mathematics of Computation,
Vol. 10,
Issue. 55,
p.
140.
Householder, Alston S.
1956.
Bibliography on Numerical Analysis.
Journal of the ACM,
Vol. 3,
Issue. 2,
p.
85.
Struble, George W.
1963.
Orthogonal polynomials: Variable-signed weight functions.
Numerische Mathematik,
Vol. 5,
Issue. 1,
p.
88.
Pohler, R. F.
and
Hanson, H. P.
1965.
Incoherent X-Ray Scattering Factors.
The Journal of Chemical Physics,
Vol. 42,
Issue. 7,
p.
2347.
1965.
The rectangle in generalized plane stress, with numerically prescribed boundary stresses and applications to discontinuous loading.
Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences,
Vol. 286,
Issue. 1405,
p.
251.
van de Vooren, A. I.
and
van Linde, H. J.
1966.
Numerical calculation of integrals with strongly oscillating integrand.
Mathematics of Computation,
Vol. 20,
Issue. 94,
p.
232.
Clendenin, W. W.
1966.
A method for numerical calculation of Fourier integrals.
Numerische Mathematik,
Vol. 8,
Issue. 5,
p.
422.
de Balbine, Guy
and
Franklin, Joel N.
1966.
The calculation of Fourier integrals.
Mathematics of Computation,
Vol. 20,
Issue. 96,
p.
570.
Murli, A.
1968.
Il calcolo numerico degli integrali trigonometrici.
Calcolo,
Vol. 5,
Issue. S2,
p.
922.
Thornton, B. S.
1968.
Damping loss in a cascade of fluttering phased aerofoils.
Journal of the Australian Mathematical Society,
Vol. 8,
Issue. 2,
p.
327.
Fosdick, Lloyd D.
1968.
A special case of the Filon quadrature formula.
Mathematics of Computation,
Vol. 22,
Issue. 101,
p.
77.
Chase, Stephen M.
and
Fosdick, Lloyd D.
1969.
An algorithm for Filon quadrature.
Communications of the ACM,
Vol. 12,
Issue. 8,
p.
453.
Lyness, J. N.
1970.
The calculation of Fourier coefficients by the Möbius inversion of the Poisson summation formula. I. Functions whose early derivatives are continuous.
Mathematics of Computation,
Vol. 24,
Issue. 109,
p.
101.
Piessens, R.
and
Poleunis, F.
1971.
A numerical method for the integration of oscillatory functions.
BIT,
Vol. 11,
Issue. 3,
p.
317.
Håvie, Tore
1973.
Remarks on an expansion for integrals of rapidly oscillating functions.
BIT,
Vol. 13,
Issue. 1,
p.
16.
Fuller, James A.
and
Wait, James R.
1973.
Mutual electromagnetic coupling of coaxial loops in a borehole.
Radio Science,
Vol. 8,
Issue. 5,
p.
453.

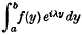 is of frequent occurrence in applied problems. Here λ is real and i is the imaginary unit. Tables of the integrals are often required for a wide range of λ values, some of which may be quite large. Tabulation of the integrand for each λ, followed by ordinary methods of numerical integration, is slow and tedious because the number of points required increases with increasing λ. In this paper formulas are given so that once
is of frequent occurrence in applied problems. Here λ is real and i is the imaginary unit. Tables of the integrals are often required for a wide range of λ values, some of which may be quite large. Tabulation of the integrand for each λ, followed by ordinary methods of numerical integration, is slow and tedious because the number of points required increases with increasing λ. In this paper formulas are given so that once 