Hostname: page-component-6bf8c574d5-m789k Total loading time: 0 Render date: 2025-03-07T03:28:38.371Z Has data issue: false hasContentIssue false
  • English
  • Français

Groups generated by two twists along spherical sequences

Part of: Special aspects of infinite or finite groups Representation theory of rings and algebras

Published online by Cambridge University Press:  16 May 2022

Y. VOLKOV
Y. VOLKOV*
Affiliation:
Department of Mathematics and Computer Sciences, Saint Petersburg State University, Saint Petersburg, 199178, Russia, Line 14th (Vasilyevsky Island), 29. e-mail: wolf86_666@list.ru
Get access Rights & Permissions [Opens in a new window]

Abstract

We describe all groups that can be generated by two twists along spherical sequences in an enhanced triangulated category. It will be shown that with one exception such a group is isomorphic to an abelian group generated by not more than two elements, the free group on two generators or the braid group of one of the types 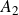$A_2$ 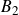, $B_2$ and 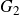$G_2$ factorised by a central subgroup. The last mentioned subgroup can be nontrivial only if some specific linear relation between length and sphericity holds. The mentioned exception can occur when one has two spherical sequences of length 3 and sphericity 2. In this case the group generated by the corresponding two spherical twists can be isomorphic to the nontrivial central extension of the symmetric group on three elements by the infinite cyclic group. Also we will apply this result to give a presentation of the derived Picard group of selfinjective algebras of the type 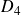$D_4$ with torsion 3 by generators and relations.

MSC classification

Secondary: 20F36: Braid groups; Artin groups 16G70: Auslander-Reiten sequences (almost split sequences) and Auslander-Reiten quivers
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 174 , Issue 1 , January 2023 , pp. 137 - 161
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Cambridge Philosophical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anno, R. and Logvinenko, T.. Spherical DG-functors. J. Eur. Math. Soc. 19 (2017), 2577–2656.CrossRefGoogle Scholar
Asashiba, H.. The derived equivalence classification of representation-finite selfinjective algebras. J. Alg. 214 (1999), 182–221.Google Scholar
Brav, C. and Thomas, H.. Braid groups and Kleinian singularities. Math. Ann. (4) 351 (2011), 1005–1017.Google Scholar
Coelho Simões, R.. Hom-configurations in triangulated categories generated by spherical objects. J. Pure Appl. Alg. (8) 219 (2015), 3322–3336.Google Scholar
Coelho Simões, R., Pauksztello, D.. Torsion pairs in a triangulated category generated by a spherical object. J. Alg. 448 (2016), 1–47.Google Scholar
Coelho Simões, R.. Mutations of simple-minded systems in Calabi-Yau categories generated by a spherical object. Forum Math. (5) 29 (2017), 1065–1081.Google Scholar
Efimov, A.. Braid group actions on triangulated categories. The Möbius contest paper (2007).Google Scholar
Happel, D.. Triangulated categories in the representation theory of finite dimensional algebras. LMS Lecture Note Series 119, (Cambridge University Press, 1988).CrossRefGoogle Scholar
Guil-Asensio, F. and Saorýn, M.. The group of outer automorphisms and the Picard group of an algebra. Alg. Rep. Theory (4) 2 (1999), 313–330.Google Scholar
Holm, T., Jørgensen, P. and Yang., D. Sparseness of t-structures and negative Calabi-Yau dimension in triangulated categories generated by a spherical object. Bull. London Math. Soc. 45 (2013), 120–130.Google Scholar
Miyachi, J. I. and Yekutieli, A.. Derived Picard groups of finite-dimensional hereditary algebras. Comp. Math. (3) 129 (2001), 341–368.Google Scholar
Mizuno, Y.. Derived Picard groups of preprojective algebras of Dynkin type. (2017) arXiv:1709.03383.Google Scholar
Pollack, R. D.. Algebras and their automorphism groups. Comm. Alg. (8) 17 (1989), 1843–1866.Google Scholar
Rickard, J.. Morita theory for derived categories. J. London Math. Soc. (3) 39 (1989), 436–456.Google Scholar
Rickard, J.. Derived equivalences as derived functors. J. London Math. Soc, (1) 43 (1991), 37–48.Google Scholar
Rouquier, R. and Zimmermann, A.. Picard groups for derived module categories. Proc. London Math. Soc. (1) 87 (2003), 197–225.Google Scholar
Segal, E.. All autoequivalences are spherical twists. Int. Math. Res. Not. (10) 2018 (2018), 3137–3154.Google Scholar
Seidel, P. and Thomas, R.. Braid group actions on derived categories of coherent sheaves. Duke Math. J. (1) 108 (2001), 37–108.Google Scholar
Volkov, Y. V. and Generalov, A.. Hochschild cohomology for self-injective algebras of tree class $D_n$ . III. Zap. Nauch. Sem. POMI 386, 100–128 (2011). Translation: J. Math. Sci. (N. Y.) (3) 180 (2012), 252–268.Google Scholar
Volkov, Y. V., Generalov, A. and Ivanov, S.. On the construction of bimodule resolutions with the help of the Happel lemma. — Zap. Nauch. Sem. POMI 375, 61–70 (2010). Translation: J. Math. Sci. (N. Y.) (3) 171 (2010), 338–343.Google Scholar
Riedtmann, C.. Algebren, Darstellungsköcher, Überlagerungen und zurück. Comment. Math. Helv. 55 (1980), 199–224.CrossRefGoogle Scholar
Volkov, Y. and Zvonareva, A.. On standard derived equivalences of orbit categories. Alg. Rep. Theory (1) 21 (2018), 195–217.Google Scholar
Volkov, Y. and Zvonareva, A.. Derived Picard groups of selfinjective Nakayama algebras. Manuscripta Math. (1) 152 (2017), 199–222.Google Scholar
Qiu, Y. and Woolf, J.. Contractible stability spaces and faithful braid group actions. Geom. Top. (6) 22 (2018), 3701–3760.Google Scholar
Yekutieli, A.. Dualizing complexes, Morita equivalence and the derived Picard group of a ring. J. London Math. Soc. (3) 60 (1999), 723–746.Google Scholar
Yekutieli, A.. The Derived Picard Group is a Locally Algebraic Group. Alg. Rep. Theory (1) 7 (2004), 53–57.Google Scholar