Article contents
Conformally invariant complete metrics
Published online by Cambridge University Press: 30 May 2022
Abstract
For a domain G in the one-point compactification 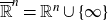 $\overline{\mathbb{R}}^n = {\mathbb{R}}^n \cup \{ \infty\}$ of
$\overline{\mathbb{R}}^n = {\mathbb{R}}^n \cup \{ \infty\}$ of 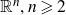 ${\mathbb{R}}^n, n \geqslant 2$, we characterise the completeness of the modulus metric
${\mathbb{R}}^n, n \geqslant 2$, we characterise the completeness of the modulus metric 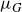 $\mu_G$ in terms of a potential-theoretic thickness condition of
$\mu_G$ in terms of a potential-theoretic thickness condition of 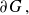 $\partial G\,,$ Martio’s M-condition [35]. Next, we prove that
$\partial G\,,$ Martio’s M-condition [35]. Next, we prove that 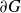 $\partial G$ is uniformly perfect if and only if
$\partial G$ is uniformly perfect if and only if 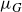 $\mu_G$ admits a minorant in terms of a Möbius invariant metric. Several applications to quasiconformal maps are given.
$\mu_G$ admits a minorant in terms of a Möbius invariant metric. Several applications to quasiconformal maps are given.
MSC classification
Information
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 174 , Issue 2 , March 2023 , pp. 273 - 300
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of Cambridge Philosophical Society
Footnotes
The authors were supported in part by JSPS KAKENHI Grant Number JP17H02847 and NSF of the Higher Education Institutions of Jiangsu Province, China, Grant Number 17KJB110015, and NSFC Grant Number 12001391.
References
- 6
- Cited by

