Collapsing three-dimensional convex polyhedra: correction
Published online by Cambridge University Press: 24 October 2008
Extract
An ingenious construction due to Connelly and Henderson (2) has shown that there exists a rectilinearly triangulated convex polyhedron P in 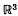 having the property that at least one vertex of the triangulation lies in the interior of a face of P, and yet there is no isomorphic triangulation of a convex polyhedron P′ all of whose vertices are vertices of P′. Thus the assertion beginning on the top line of p. 354 of (1) is false, which leaves a gap in the proof of essentially the main result of (1), namely that any rectilinearly triangulated convex polyhedron in
having the property that at least one vertex of the triangulation lies in the interior of a face of P, and yet there is no isomorphic triangulation of a convex polyhedron P′ all of whose vertices are vertices of P′. Thus the assertion beginning on the top line of p. 354 of (1) is false, which leaves a gap in the proof of essentially the main result of (1), namely that any rectilinearly triangulated convex polyhedron in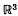 can be simplicially collapsed onto its boundary minus a 2-simplex σ. The purpose of this note is to show that the theorem is nevertheless still true. In any case the Corollaries 2 and 3 in (1) are unaffected by the error.
can be simplicially collapsed onto its boundary minus a 2-simplex σ. The purpose of this note is to show that the theorem is nevertheless still true. In any case the Corollaries 2 and 3 in (1) are unaffected by the error.
Information
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 88 , Issue 2 , September 1980 , pp. 307 - 310
- Copyright
- Copyright © Cambridge Philosophical Society 1980
References
REFERENCES
- 3
- Cited by

