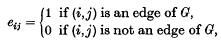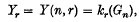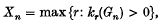Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Chvátal, V.
1977.
Determining the Stability Number of a Graph.
SIAM Journal on Computing,
Vol. 6,
Issue. 4,
p.
643.
Bollobás, B.
Catlin, P.A.
and
Erdös, P.
1980.
Hadwiger's Conjecture is True for Almost Every Graph.
European Journal of Combinatorics,
Vol. 1,
Issue. 3,
p.
195.
Bollobás, Béla
1981.
The diameter of random graphs.
Transactions of the American Mathematical Society,
Vol. 267,
Issue. 1,
p.
41.
Bollobás, Béla
and
Thomason, Andrew
1981.
Graphs which Contain all Small Graphs.
European Journal of Combinatorics,
Vol. 2,
Issue. 1,
p.
13.
Lueker, George S.
1981.
Optimization Problems on Graphs with Independent Random Edge Weights.
SIAM Journal on Computing,
Vol. 10,
Issue. 2,
p.
338.
Bollobás, Béla
1981.
Degree sequences of random graphs.
Discrete Mathematics,
Vol. 33,
Issue. 1,
p.
1.
Bartusch, M.
1981.
An algorithm for generating all maximal independent subsets of posets.
Computing,
Vol. 26,
Issue. 4,
p.
343.
Ausiello, G.
and
Protasi, M.
1981.
Fundamentals of Computation Theory.
Vol. 117,
Issue. ,
p.
24.
Slominski, L.
1982.
Probabilistic analysis of combinatorial algorithms: A bibliography with selected annotations.
Computing,
Vol. 28,
Issue. 3,
p.
257.
Lueker, George S.
1982.
Applied Probability-Computer Science: The Interface Volume 1.
p.
489.
Karoński, Michał
1982.
A review of random graphs.
Journal of Graph Theory,
Vol. 6,
Issue. 4,
p.
349.
Kelly, Douglas G.
and
Oxley, James G.
1982.
Asymptotic properties of random subsets of projective spaces.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 91,
Issue. 1,
p.
119.
Lueker, George S.
1982.
Applied Probability-Computer Science: The Interface Volume 1.
p.
489.
Pittel, B.
1982.
On the probable behaviour of some algorithms for finding the stability number of a graph.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 92,
Issue. 3,
p.
511.
McDiarmid, Colin
1982.
Achromatic numbers of random graphs.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 92,
Issue. 1,
p.
21.
Oberschelp, W.
1982.
Combinatorial Theory.
Vol. 969,
Issue. ,
p.
276.
Erdös, P.
and
Palka, Z.
1983.
Trees in random graphs.
Discrete Mathematics,
Vol. 46,
Issue. 2,
p.
145.
Marchetti-Spaccamela, A.
and
Talamo, M.
1983.
CAAP'83.
Vol. 159,
Issue. ,
p.
332.
Marchetti-Spaccamela, Alberto
and
Protasi, Marco
1983.
The largest tree in a random graph.
Theoretical Computer Science,
Vol. 23,
Issue. 3,
p.
273.
Protasi, Marco
and
Talamo, Maurizio
1983.
Foundations of Computation Theory.
Vol. 158,
Issue. ,
p.
360.
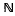 , the set of natural numbers, such that each edge occurs with probability p, independently of all other edges. In other words the random variables eij, 1 ≤ i < j, defined by
, the set of natural numbers, such that each edge occurs with probability p, independently of all other edges. In other words the random variables eij, 1 ≤ i < j, defined by