Hostname: page-component-745bb68f8f-f46jp Total loading time: 0 Render date: 2025-01-11T19:52:31.582Z Has data issue: false hasContentIssue false
  • English
  • Français

Centers and Azumaya loci for finite W-algebras in positive characteristic

Part of: Lie algebras and Lie superalgebras

Published online by Cambridge University Press:  24 May 2021

BIN SHU  and
YANG ZENG
BIN SHU
Affiliation:
School of Mathematical Sciences, East China Normal University, No. 500, Dongchuan Road, Shanghai 200241, P. R. China e-mail: bshu@@math.ecnu.edu.cn
YANG ZENG
Affiliation:
School of Statistics and Data Science, Nanjing Audit University, No. 86 West Yushan Road, Jiangpu Street, Pukou District, Nanjing, Jiangsu Province 211815, P. R. China e-mail: zengyang@nau.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we study the center Z of the finite W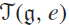-algebra $${\mathcal{T}}({\mathfrak{g}},e)$$ associated with a semi-simple Lie algebra 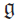$$\mathfrak{g}$$ over an algebraically closed field 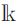$$\mathbb{k}$$ of characteristic p≫0, and an arbitrarily given nilpotent element 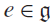$$e \in{\mathfrak{g}} $$ We obtain an analogue of Veldkamp’s theorem on the center. For the maximal spectrum Specm(Z), we show that its Azumaya locus coincides with its smooth locus of smooth points. The former locus reflects irreducible representations of maximal dimension for 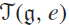$${\mathcal{T}}({\mathfrak{g}},e)$$ .

MSC classification

Primary: 17B50: Modular Lie (super)algebras
Secondary: 17B05: Structure theory 17B08: Coadjoint orbits; nilpotent varieties
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 173 , Issue 1 , July 2022 , pp. 35 - 66
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of Cambridge Philosophical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Atiyah, M. F. and Macdonald, I. G.. Introduction to Commutative Algebras (Addison-Wesley publishing company, Reading, Massachusetts, Menlo Park, California/London/Don Mills, Ontario) (1969).Google Scholar
Björk, J. E.. The Auslander condition on Noetherian rings. Seminaire Dubreil–Malliavin 1987-88, Lecture Notes in Math. 1404 (Springer, 1989), 137–173.Google Scholar
Brown, K. A. and Goodearl, K. R.. Homological aspects of Noetherian PI Hopf algebras and irreducible modules of maximal dimension. J. Algebra 198 (1997), 240–265.CrossRefGoogle Scholar
Brown, K. A. and Gordon, I.. The ramification of centres: Lie algebras in positive characteristic and quantised enveloping algebras. Math. Z. 238 (2001), 733–779.CrossRefGoogle Scholar
Carter, R. W.. Finite groups of Lie type: conjugacy classes and complex characters (John Wiley & Sons, 1985).Google Scholar
Drozd, Y. A. and Kirichenko, V. V.. Finite dimensional algebras. Translated from the Russian by Vlastimil Dlab (Springer-Verlag, Berlin/Heidelberg/New York/London/Paris/Tokyo/Hong Kong/Barcelona/Budapest, 1994).CrossRefGoogle Scholar
Gan, W. L. and Ginzburg, V.. Quantization of Slodowy slices. Internat. Math. Res. Notices 5 (2002), 243–255.CrossRefGoogle Scholar
Goodearl, K. R and Warfiled, R. B. An introduction to noncommutative Noetherian rings. no. 16 London Math. Soc. Student Texts (Cambridge University Press, 1989).Google Scholar
Goodwin, S. M. and Topley, L. W.. Modular finite W-algebras. Internat. Math. Res. Notices 18 (2019), 5811–5853.CrossRefGoogle Scholar
Goodwin, S. M. and Topley, L. W.. Restricted shifted Yangians and restricted finite W-algebras. Trans. Amer. Math. Soc. Series B vol. 8 (2021), 190–228.CrossRefGoogle Scholar
Jacobson, N.. Basic Algebra II (W. H. Freeman and Company, San Francisco, 1980).Google Scholar
Jacobson, N.. Lectures in abstract algebra, III. (Van Nostrand, Princeton, 1964).10.1007/978-1-4612-9872-4CrossRefGoogle Scholar
Jantzen, J. C.. Representations of Lie algebras in prime characteristic, in: Representation Theories and Algebraic Geometry, Proc. Montréal (NATO ASI series C 524) (1997), 185–235.CrossRefGoogle Scholar
Jantzen, J. C.. Nilpotent orbits in representation theory. Progr. Math. vol. 228 (Birkhäuser 2004).Google Scholar
Kac, V. and Weisfeiler, B.. Coadjoint action of a semi-simple algebraic group and the center of the enveloping algebra in characteristic p. Indag. Math. 38 (1976), 136–151.CrossRefGoogle Scholar
Kostant, B.. On Whittaker modules and representation theory. Invent. Math. 48 (1978), 101–184.CrossRefGoogle Scholar
Losev, I.. Quantized symplectic actions and W-algebras. J. Amer. Math. Soc. 23 (2010), 35–59.10.1090/S0894-0347-09-00648-1CrossRefGoogle Scholar
Lynch, T. E.. Generalized Whittaker vectors and representation theory. PhD. thesis. M. I. T. (1979).Google Scholar
McConnell, J. C. and Robson, J. C.. Noncommutative Noetherian Rings (John Wiley & Sons Ltd, Chichester/New York/Brisbane/Toronto/Singapore, 1988).Google Scholar
Mirković, I. and Rumynin, D.. Centers of reduced enveloping algebras. Math. Z. 231 (1999), 123–132.10.1007/PL00004719CrossRefGoogle Scholar
Mil’ner, A. A.. Irreducible representations of modular Lie algebras. Math. USSR-Izv. 9 (1975), 1169–1187.CrossRefGoogle Scholar
Pierce, R. S.. Associative Algebras. Graduate Texts in Math. (Springer, New York/Heidelberg/Berlin, 1982).CrossRefGoogle Scholar
Premet, A. and Skryabin, S.. Representations of restricted Lie algebras and families of associative $$\mathfrak{L}$$ -algebras. J. Reine Angew. Math. 507 (1999), 189–218.CrossRefGoogle Scholar
Premet, A. Complexity of Lie algebra representations and nilpotent elements of the stabilizers of linear forms. Math. Z. 228 (1998), 255–282.CrossRefGoogle Scholar
Premet, A.. Irreducible representations of Lie algebras of reductive groups and the Kac-Weisfeiler conjecture. Invent. Math. 121 (1995), 79–117.CrossRefGoogle Scholar
Premet, A.. Special transverse slices and their enveloping algebras. Advances in Math. 170 (2002), 1–55.CrossRefGoogle Scholar
. Premet, A. Enveloping algebras of Slodowy slices and the Joseph ideal. J. Eur. Math. Soc. 9 (2007), 487–543.CrossRefGoogle Scholar
. Premet, A. Primitive ideals, non-restricted representations and finite W-algebras. Mosc. Math. J. 7 (2007), 743–762.Google Scholar
Premet, A.. Commutative quotients of finite W-algebras. Advances in Math. 225 (2010), 269–306.CrossRefGoogle Scholar
Premet, A.. Enveloping algebras of Slodowy slices and Goldie rank. Transform. Groups 16 (2011), 857–888.CrossRefGoogle Scholar
Shafarevich, I. R.. Basic Algebraic Geometry vol. 1 (Springer-Verlag, Berlin/Heidelberg/New York, 1977, 1994).Google Scholar
Skryabin, S.. Representations of the Poisson algebra in prime characteristic. Math. Z. 243 (2003), 563–597.CrossRefGoogle Scholar
Slodowy, P.. Simple singularities and simple algebraic groups. Lecture Notes in Math. 815 (Springer-Verlag, Berlin/Heidelberg/New York, 1980).Google Scholar
Stafford, J. T. and Zhang, J. J.. Homological properties of graded Noetherian PI rings. J. Algebra 168 (1994), 988–1026.CrossRefGoogle Scholar
Serre, J.-P.. Algebre locale—Multiplicites. Lecture Notes in Math. vol. 11 (Springer-Verlag, Berlin/New York, 1975).Google Scholar
Strade, H. and Farnsteiner, R.. Modular Lie algebras and their representations. Monog. Textbooks Pure and Appl. Math. vol. 116 (Marcel Dekker, Inc., New York/Basel, 1988).Google Scholar
Teo, K.-M.. Homological properties of fully bounded Noetherian rings. J. London Math. Soc. 255 (1997), 37–54.CrossRefGoogle Scholar
Veldkamp, F. D.. The center of the universal enveloping algebra of a Lie algebra in characteristic p. Ann. Sci. Ecole Norm. Sup. 5 (1972), 217–240.CrossRefGoogle Scholar
Zassenhaus, H.. The representations of Lie algebras of prime characteristic. Proc. Glasgow Math. Assoc. 2 (1954), 1–36.10.1017/S2040618500032974CrossRefGoogle Scholar