No CrossRef data available.
Article contents
Restricted projections to lines in 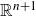 $\mathbb{R}^{n+1}$
$\mathbb{R}^{n+1}$
Published online by Cambridge University Press: 15 May 2025
Abstract
We prove the following restricted projection theorem. Let 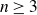 $n\ge 3$ and
$n\ge 3$ and 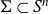 $\Sigma \subset S^{n}$ be an
$\Sigma \subset S^{n}$ be an  $(n-1)$-dimensional
$(n-1)$-dimensional 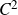 $C^2$ manifold such that
$C^2$ manifold such that 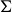 $\Sigma$ has sectional curvature
$\Sigma$ has sectional curvature  $\gt1$. Let
$\gt1$. Let 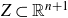 $Z \subset \mathbb{R}^{n+1}$ be analytic and let
$Z \subset \mathbb{R}^{n+1}$ be analytic and let 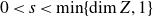 $0 \lt s \lt \min\{\dim Z, 1\}$. Then
$0 \lt s \lt \min\{\dim Z, 1\}$. Then 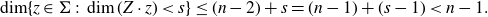 \begin{equation*} \dim \{z \in \Sigma\; :\; \dim (Z \cdot z) \lt s\} \le (n-2)+s = (n-1) + (s-1) \lt n-1.\end{equation*}
\begin{equation*} \dim \{z \in \Sigma\; :\; \dim (Z \cdot z) \lt s\} \le (n-2)+s = (n-1) + (s-1) \lt n-1.\end{equation*}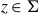 $z \in \Sigma$,
$z \in \Sigma$, 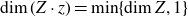 $\dim (Z \cdot z) = \min\{\dim Z, 1\}$.
$\dim (Z \cdot z) = \min\{\dim Z, 1\}$.
The core idea, originated from Käenmäki–Orponen–Venieri, is to transfer the restricted projection problem to the study of the dimension lower bound of Furstenberg sets of cinematic family contained in 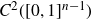 $C^2([0,1]^{n-1})$. This cinematic family of functions with multivariables are extensions of those of one variable by Pramanik–Yang–Zahl and Sogge. Since the Furstenberg sets of cinematic family contain the affine Furstenberg sets as a special case, the dimension lower bound of Furstenberg sets improves the one by Héra, Héra–Keleti–Máthé and Dąbrowski–Orponen–Villa.
$C^2([0,1]^{n-1})$. This cinematic family of functions with multivariables are extensions of those of one variable by Pramanik–Yang–Zahl and Sogge. Since the Furstenberg sets of cinematic family contain the affine Furstenberg sets as a special case, the dimension lower bound of Furstenberg sets improves the one by Héra, Héra–Keleti–Máthé and Dąbrowski–Orponen–Villa.
Moreover, our method to show the restricted projection theorem can also give a new proof for the Mattila projection theorem in 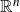 $\mathbb{R}^n$ with
$\mathbb{R}^n$ with 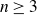 $n \ge 3$.
$n \ge 3$.
Information
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 179 , Issue 1 , July 2025 , pp. 105 - 143
- Copyright
- © The Author(s), 2025. Published by Cambridge University Press on behalf of Cambridge Philosophical Society

