Hostname: page-component-5b777bbd6c-f9nfp Total loading time: 0 Render date: 2025-06-18T19:40:24.848Z Has data issue: false hasContentIssue false
  • English
  • Français

Orbifold Euler characteristics for compactified universal Jacobians over 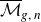$\overline{\mathcal{M}}_{g,\,n}$

Part of: Curves Abelian varieties and schemes

Published online by Cambridge University Press:  13 May 2025

SOFIA WOOD
SOFIA WOOD*
Affiliation:
Department of Mathematics, Columbia University, 2990 Broadway, New York, NY 10027, U.S.A. e-mail: sw3987@columbia.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We calculate the orbifold Euler characteristics of all the degree d fine universal compactified Jacobians over the moduli space of stable curves of genus g with n marked points, as defined by Pagani and Tommasi. We show that this orbifold Euler characteristic agrees with the Euler characteristic of 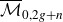$\overline{\mathcal{M}}_{0, 2g+n}$ up to a combinatorial factor, and in particular, is independent of the degree d and the choice of degree d fine compactified universal Jacobian.

MSC classification

Primary: 14H10: Families, moduli (algebraic)
Secondary: 14K10: Algebraic moduli, classification
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 179 , Issue 1 , July 2025 , pp. 1 - 16
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Cambridge Philosophical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Alexeev, V.. Compactifled Jacobians and Torelli map. Publ. Res. Inst. Math. Sci. 40 (2004), 1241–1265.CrossRefGoogle Scholar
Arbarello, E., Cornalba, M. and Griffiths, P.. Geometry of Algebraic Curves, vol. II (Springer-Verlag, 2011).CrossRefGoogle Scholar
Alper, J.. Stacks and moduli. https://sites.math.washington.edu/jarod/moduli.pdf Google Scholar
Bae, Y., Holmes, D., Pandharipande, R., Schmitt, J. and Schwarz, R.. Pixton’s formula and Abel-Jacobi theory on the Picard stack. Acta Math., 230 (2023), 205–319.CrossRefGoogle Scholar
Beauville, A.. Counting rational curves on ${\text{K3}}$ surfaces. Duke Math. J., Duke University Press, 97 (1999), 99–108.Google Scholar
Bejleri, D.. Deformation theory of line bundles, compactified Jacobians and integral curves, (2020). https://people.math.harvard.edu/bejleri/teaching/math259xfa19/math259x_lecture19-21.pdf.Google Scholar
Bini, G. and Harer, J.. The Euler characteristic of the moduli space of curves. Invent. Math., 85 (1986), 457–485.Google Scholar
Caporaso, L.. A compactification of the universal Picard variety over the moduli space of stable curves. Algebraic Geometry, 3 (1994), 589–660.Google Scholar
Constantini, M., Möller, M. and Zachhuber, Jonathan. The Chern classes and Euler characteristic of the moduli spaces of Abelian differentials. Forum of Mathematics, Pi 10 (2022), 1–55.Google Scholar
Estaves, E.. Compactifying the relative Jacobian over families of reduced curves. Trans. Amer. Math. Soc. 353 (1994), 3045–3095.CrossRefGoogle Scholar
Esteves, E., Gagne, M. and Kleiman, S.. Abel Maps and presentation schemes. Comm. Algebra, 28 (2007), 5961–5992.CrossRefGoogle Scholar
Harer, J. and Zagier, D.. The Euler characteristic of the moduli space of curves. Invent. Math. 85 (1986), 457–485.CrossRefGoogle Scholar
Hartshorne, R.. Algebraic Geometry, Springer, (1977).Google Scholar
Holmes, D., Kass, J. L. and Pagani, N.. Extending the double ramification cycle using Jacobians. European Journal of Mathematics, 4 (2018), 1087–1099.CrossRefGoogle Scholar
Holmes, D., Molcho, S., Pandharipande, R., Pixton, A. and Schmitt, J.. Logarithmic double ramification cycles. Preprint: ArXiv:2207.06778 (2024).CrossRefGoogle Scholar
Kass, J. L. and Pagani, N.. Extensions of the universal theta divisor. Adv. Math. 321 (2017), 221–268.CrossRefGoogle Scholar
Kass, J. and Pagani, N.. The stability space of compactified universal Jacobians. Trans. Amer. Math. Soc. 372 (2019), 4851–4887.CrossRefGoogle Scholar
Melo, M., Compactifications of the universal Jacobian over curves with marked points. Preprint: ArXiv:1509.06177 (2016).Google Scholar
Melo, M. and Viviani, F.. Fine compactified Jacobians. Math. Nachr., 285 (2012), 997–1031.CrossRefGoogle Scholar
Pagani, N. and Tommasi, O.. Geometry of genus one fine Compactified universal Jacobians. Internat. Math. Res. Not. 0 (2022), 1–49.Google Scholar
Pagani, N. and Tommasi, O.. Stability conditions for line bundles on nodal curves. Preprint: ArXiv:2309.08509 (2004).Google Scholar
Pandharipande, R.. A compactification over $\overline{M}_g$ of the universal moduli space of slope-semistable vector bundles, J. Amer. Math. Soc. 9 (1996), 425–471.CrossRefGoogle Scholar
Simpson, C. T.. Moduli of representations of the fundamental group of a smooth projective variety. Publ. Math. Inst. Hautés Etudés Sci. 3 (1994), 47–129.CrossRefGoogle Scholar
Spanier, E. H.. Algebraic Topology (Springer-Verlag, 1921).Google Scholar
Yin, Q.. Cycles on curves and Jacobians: a tale of two tautological rings. Algebraic Geometry, 3 (2016), 179–210.CrossRefGoogle Scholar
Vistoli, A.. Intersection theory on algebraic stacks and on their moduli spaces. Invent. Math. 97 (1989), 613–670.CrossRefGoogle Scholar
El, F.. Zein. Topology of algebraic morphisms, (2008). https://webusers.imj-prg.fr/fouad.elzein/Contemporary.pdf#page.Google Scholar