No CrossRef data available.
Article contents
On Λ-Ω-extendable distributions
Published online by Cambridge University Press: 24 October 2008
Abstract
Let Λ ⊂ Ω ⊂ ℝnbe open subsets. We construct a natural space 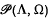 of test functions on Λ such that the dual
of test functions on Λ such that the dual 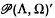 consists exactly of those distributions on Λ which can be extended to distributions on Ω. As an application of this representation we calculate the space
consists exactly of those distributions on Λ which can be extended to distributions on Ω. As an application of this representation we calculate the space 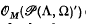 of multiplication operators on
of multiplication operators on 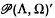 as well as the space
as well as the space 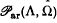 of absolutely regular extendable distributions.
of absolutely regular extendable distributions.
Information
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 99 , Issue 1 , January 1986 , pp. 135 - 142
- Copyright
- Copyright © Cambridge Philosophical Society 1986
References
REFERENCES
[2]Dierolf, P.. Multiplication and convolution operators between spaces of distributions. In Functional Analysis: Surveys and Recent Results, vol. III, ed. Bierstedt, K. D. and Fuchssteiner, B. (North-Holland Publ. Comp., 1984), pp. 305–330.Google Scholar
[3]Dierolf, P.. Some locally convex spaces of regular distributions. Studia Math. 77 (1984), 393–412.CrossRefGoogle Scholar
[4]Dierolf, P. and Voigt, J.. Calculation of the bidual for some function spaces. Integrable distributions. Math. Ann. 253 (1980), 63–87.Google Scholar
[5]Dierolf, S. and Schwanengel, U.. Examples of locally compact non-compact minimal topological groups. Pacific J. Math. 82 (1979), 249–355.CrossRefGoogle Scholar
[6]Floret, K.. Some aspects of the theory of locally convex inductive limits. In Functional Analysis: Surveys and Recent Results, vol. II, ed. Bierstedt, K. D. and Fuchssteiner, B. (North-Holland Publ. Comp., 1980), pp. 205–237.CrossRefGoogle Scholar
[7]Grothendieck, A.. Produits tensoriels topologiques et espaces nucléaires. Memoirs Amer. Math. Soc. 16 (1966).Google Scholar
[8]Horvath, J.. Topological vector spaces and distributions (Addison-Wesley Publishing Company, 1966).Google Scholar
[9]Łojasiewicz, S.. Sur le probleme de division. Studia Math. 18 (1959), 87–136.CrossRefGoogle Scholar
[10]Schwartz, L.. Théorie des distributions à valeurs vectorielles. Ann. Inst. Fourier Grenóble 7 (1957), 1–141.CrossRefGoogle Scholar
[11]Schwartz, L.. Some applications of the theory of distributions. In Lectures on Modern Mathematics, ed. Saaty, T. L. (J. Wiley, 1963), pp. 23–58.Google Scholar
[13]Valdivia, M.. Sobre el espacio ℬ0(Ω). Rev. Real. Acad. Ci. Exact. Fis. Natur. Madrid 74 (1980), 835–863.Google Scholar
[14]Vogt, D.. Sequence space representations of spaces of test functions and distributions. In Functional Analysis, Holomorphy and Approximation Theory, ed. Zapata, G. I. (Marcel Dekker, 1983).Google Scholar
[15]Voigt, J.. Factorization in some Fréchet algebras of differentiable functions. Studia Math. 77 (1984), 333–348.CrossRefGoogle Scholar

