Article contents
Images of fractional Brownian motion with deterministic drift: Positive Lebesgue measure and non-empty interior
Published online by Cambridge University Press: 28 February 2022
Abstract
Let 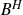 $B^{H}$ be a fractional Brownian motion in
$B^{H}$ be a fractional Brownian motion in 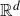 $\mathbb{R}^{d}$ of Hurst index
$\mathbb{R}^{d}$ of Hurst index 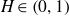 $H\in\left(0,1\right)$,
$H\in\left(0,1\right)$,  $f\;:\;\left[0,1\right]\longrightarrow\mathbb{R}^{d}$ a Borel function and
$f\;:\;\left[0,1\right]\longrightarrow\mathbb{R}^{d}$ a Borel function and 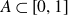 $A\subset\left[0,1\right]$ a Borel set. We provide sufficient conditions for the image
$A\subset\left[0,1\right]$ a Borel set. We provide sufficient conditions for the image 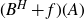 $(B^{H}+f)(A)$ to have a positive Lebesgue measure or to have a non-empty interior. This is done through the study of the properties of the density of the occupation measure of
$(B^{H}+f)(A)$ to have a positive Lebesgue measure or to have a non-empty interior. This is done through the study of the properties of the density of the occupation measure of 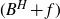 $(B^{H}+f)$. Precisely, we prove that if the parabolic Hausdorff dimension of the graph of f is greater than Hd, then the density is a square integrable function. If, on the other hand, the Hausdorff dimension of A is greater than Hd, then it even admits a continuous version. This allows us to establish the result already cited.
$(B^{H}+f)$. Precisely, we prove that if the parabolic Hausdorff dimension of the graph of f is greater than Hd, then the density is a square integrable function. If, on the other hand, the Hausdorff dimension of A is greater than Hd, then it even admits a continuous version. This allows us to establish the result already cited.
MSC classification
Information
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 173 , Issue 3 , November 2022 , pp. 693 - 713
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of Cambridge Philosophical Society
References
- 4
- Cited by

