No CrossRef data available.
Article contents
Dynamics of generalised exponential maps
Published online by Cambridge University Press: 21 April 2022
Abstract
Since 1984, many authors have studied the dynamics of maps of the form 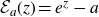 $\mathcal{E}_a(z) = e^z - a$, with
$\mathcal{E}_a(z) = e^z - a$, with 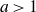 $a > 1$. It is now well-known that the Julia set of such a map has an intricate topological structure known as a Cantor bouquet, and much is known about the dynamical properties of these functions.
$a > 1$. It is now well-known that the Julia set of such a map has an intricate topological structure known as a Cantor bouquet, and much is known about the dynamical properties of these functions.
It is rather surprising that many of the interesting dynamical properties of the maps 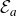 $\mathcal{E}_a$ actually arise from their elementary function theoretic structure, rather than as a result of analyticity. We show this by studying a large class of continuous
$\mathcal{E}_a$ actually arise from their elementary function theoretic structure, rather than as a result of analyticity. We show this by studying a large class of continuous 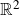 $\mathbb{R}^2$ maps, which, in general, are not even quasiregular, but are somehow analogous to
$\mathbb{R}^2$ maps, which, in general, are not even quasiregular, but are somehow analogous to 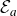 $\mathcal{E}_a$. We define analogues of the Fatou and the Julia set and we prove that this class has very similar dynamical properties to those of
$\mathcal{E}_a$. We define analogues of the Fatou and the Julia set and we prove that this class has very similar dynamical properties to those of 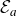 $\mathcal{E}_a$, including the Cantor bouquet structure, which is closely related to several topological properties of the endpoints of the Julia set.
$\mathcal{E}_a$, including the Cantor bouquet structure, which is closely related to several topological properties of the endpoints of the Julia set.
Information
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 174 , Issue 1 , January 2023 , pp. 123 - 136
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of Cambridge Philosophical Society
Footnotes
Supported by Engineering and Physical Sciences Research Council grant EP/R010560/1.

