No CrossRef data available.
Article contents
Braid groups, mapping class groups and their homology with twisted coefficients
Part of:
Fiber spaces and bundles
Special aspects of infinite or finite groups
Homology and cohomology theories
Published online by Cambridge University Press: 05 April 2021
Abstract
We consider the Birman–Hilden inclusion 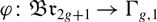 $\phi\colon\Br_{2g+1}\to\Gamma_{g,1}$ of the braid group into the mapping class group of an orientable surface with boundary, and prove that
$\phi\colon\Br_{2g+1}\to\Gamma_{g,1}$ of the braid group into the mapping class group of an orientable surface with boundary, and prove that 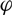 $\phi$ is stably trivial in homology with twisted coefficients in the symplectic representation
$\phi$ is stably trivial in homology with twisted coefficients in the symplectic representation 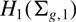 $H_1(\Sigma_{g,1})$ of the mapping class group; this generalises a result of Song and Tillmann regarding homology with constant coefficients. Furthermore we show that the stable homology of the braid group with coefficients in
$H_1(\Sigma_{g,1})$ of the mapping class group; this generalises a result of Song and Tillmann regarding homology with constant coefficients. Furthermore we show that the stable homology of the braid group with coefficients in 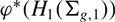 $\phi^*(H_1(\Sigma_{g,1}))$ has only 4-torsion.
$\phi^*(H_1(\Sigma_{g,1}))$ has only 4-torsion.
Information
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 172 , Issue 2 , March 2022 , pp. 249 - 266
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press on behalf of Cambridge Philosophical Society
References
Artin, E.. Theorie der Zöpfe. Abhandlungen aus dem Math. Sem. der Univ. Hamburg, 4 (1925), 47–72.CrossRefGoogle Scholar
Bianchi, A.. Embeddings of braid groups into mapping class groups. Master’s thesis, University of Pisa (2016), https://etd.adm.unipi.it/t/etd-06172016-101920/.Google Scholar
Birman, J. and Hilden, H.. On isotopies of homeomorphisms of Riemann surfaces. Ann. of Math. 97 (1973), 424–439.CrossRefGoogle Scholar
Bödigheimer, C. F. and Tillmann, U.. Embeddings of braid groups into mapping class groups and their homology. Configuration Spaces: Geometry, Combinatorics and Topology (2012), 173–191.CrossRefGoogle Scholar
Boldsen, S. K.. Improved homological stability for the mapping class group with integral or twisted coefficients. Math. Zeit. 270 (2012), 297–329.CrossRefGoogle Scholar
Callegaro, F. and Salvetti, M.. Homology of the family of hyperelliptic curves. Israel J. Math. 230 (2019), 653–692.CrossRefGoogle Scholar
Callegaro, F. and Salvetti, M.. Families of superelliptic curves, complex braid groups and generalized dehn twists. Israel J. Math. 238 (2020), 945–1000.CrossRefGoogle Scholar
Earle, C. J. and Schatz, A.. Teichmüller theory for surfaces with boundary. J. Differtial Geom. 4 (1970), 169–185.Google Scholar
Fadell, E. and Neuwirth, L.. Configuration spaces. Math. Scan. 10 (1962), 111–118.CrossRefGoogle Scholar
Farb, B. and Margalit, D.. A Primer on Mapping Class Groups (Princeton University Press, 2012).Google Scholar
Harer, J.. Stability of the homology of the mapping class group of orientable surfaces. Ann. of Math. 121 (1985), 215–249.CrossRefGoogle Scholar
Randal-Williams, O.. Resolutions of moduli spaces and homological stability. J. Eur. Math. Soc. 18 (2016), 1–81.CrossRefGoogle Scholar
Segal, G. and Tillmann, U.. Mapping configuration spaces to moduli spaces. Adv. Stud. in Pure Math. 52 (2008), 469–477.CrossRefGoogle Scholar
Song, Y. and Tillmann, U.. Braids, mapping class groups, and categorical delooping. Math. Ann. 339 (2007), 377–393.CrossRefGoogle Scholar
Vassiliev, V. A.. Complements of discriminants of smooth maps: topology and applications. (AMS, Providence, 1992).CrossRefGoogle Scholar
Vershinin, V. V.. Thom spectra of generalized braid groups. J. London Math. Soc. 61 (2000), 245–258.CrossRefGoogle Scholar

