An example in the theory of solubl groups
Published online by Cambridge University Press: 24 October 2008
Extract
Let G be a finite soluble group. In (1) Alperin proves that two system normalizers of G contained in the same Carter subgroup C of G are conjugate in C. In recent unpublished work G.A.Chambers of the University of Wisconsin has proved that, if 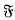 is a saturated formation, the
is a saturated formation, the 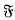 -normalizers of an A-group are pronormal subgruops; hence, in particular, that two
-normalizers of an A-group are pronormal subgruops; hence, in particular, that two 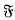 -normalizers contained in an
-normalizers contained in an 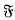 -projector E of an A-group are conjugate in E. In this note we describe an example which shows that in Alperin's theorem the class
-projector E of an A-group are conjugate in E. In this note we describe an example which shows that in Alperin's theorem the class 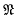 of nilpotent groups cannot in general be replaced by an arbitary saturated formation without some restriction on the class of soluble groups under consideration. we prove
of nilpotent groups cannot in general be replaced by an arbitary saturated formation without some restriction on the class of soluble groups under consideration. we prove
PROPOSITION. There exists a saturated formation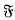 and a group G which has two
and a group G which has two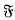 -normalizers E1and E2contained in an
-normalizers E1and E2contained in an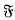 -projector F of G such that E1and E2are not conjugate in F.
-projector F of G such that E1and E2are not conjugate in F.
Information
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 67 , Issue 1 , January 1970 , pp. 13 - 16
- Copyright
- Copyright © Cambridge Philosophical Society 1970
References
REFERENCES
- 3
- Cited by

