The motivation for this article was the desire to make the cosine rule in some way geometrically “obvious”. What we have ended up with is a mixture of inductive and deductive approaches which we hope goes some way to illuminating the cosine rule, and to enhancing students' relational understanding of it. The germ of these ideas can be sown soon after students have met Pythagoras, with the question “O.K., suppose the triangle ABC is not rightangled: what can we say about a2, b2 and c2 now?”

A familiar result is that in any group of six people there are three who either all know each other or are all strangers to each other. This can be reformulated to say that, if six points are marked on a piece of paper and every pair of points is joined by a red or blue line, then there will be a monochromatic triangle, i.e. one which is all red or all blue. This result is related to a theorem which the Cambridge philosopher Frank Ramsey proved in 1930.

The set of whole numbers less than and coprime to n, with the operation of multiplication modulo n, forms an Abelian group (try to prove it for yourselves). We'll write Mn for this group, and call all such groups modulo groups or M-groups. M-groups are easy to compute. It is also particularly easy to calculate quotient groups of M-groups, making them a good source of examples and practice for the beginner. There are also some very hard, possibly unsolved, problems in classifying M-groups. In attacking such problems there is an interaction between number theoretical and group theoretical arguments which makes this a rich topic, for projects or personal pleasure.

Even the purest of pure mathematics can have a crucial influence on practical problems. In this article we show how a topic in pure mathematics (modular arithmetic) originally pursued for its own interest only, turns out to have unexpected application to an area of communication theory (cryptography). The fact that at the present time it is easy to construct large prime numbers but very difficult to factorise large composite numbers has made it possible to devise simple codes which are uncrackable by known methods.

While I worked at Teeside Polytechnic I had some difficulty in arriving in the morning by 9.00. Not being an early bird my desire was to pull into the carpark at 8.58, but this I did not seem able to achieve. If I left home at 8.15 the journey was smooth and trouble-free, and I was at my parking place by 8.50. Whereas if I left a moment later there were a couple more cars at the estate exit, each succeeding roundabout and set of traffic lights was busier, and eventually I drove into the car-park at 9.05—not only five minutes late, but also quite likely finding the spaces all full and having to resort to street parking. It seemed that no matter how I varied my start time the arrival interval of 8.50 to 9.05 was somehow inaccessible to me. Of course some people did arrive in this interval—if I did the sensible thing and left early I enviously watched them arrive at the time I would have wished. But they did not start from where I started. So I was drawn to the belief that the relationship between start and arrival time was a genuine discontinuous function, and not simply a continuous function with a rather steep critical section. Maybe the catastrophe theorists could analyse this further (but to call my misfortune a catastrophe would be a bit strong).

This perennial problem has led to many articles in the Gazette (listed by Sullivan in the June 1987 edition) many of them geometric or combinatorial in nature. If we look at some older algebra texts, published before the 1960s say, we see that the method of differences is one of the standard methods for dealing with the problem. With the current interest in discrete mathematics this method merits re-examination. A feature of the method is its effectiveness in finding the solution to the problem for all powers and it is not limited to the sums of squares and cubes. In this article we hope to show that it can be treated more transparently using the calculus of finite differences.

Here is an interesting result on sequences amenable to investigation and proof in the classroom. Consider the sequence

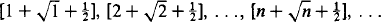
where, as usual, [x] denotes the integer part of x. You will find that you get the sequence

which consists of the natural numbers with the perfect squares omitted. This result is due to H. Halberstam [1] and in this article we verify it and look for generalisations to sequences which omit mth powers.