Hostname: page-component-5b777bbd6c-sbgtn Total loading time: 0 Render date: 2025-06-21T20:28:51.749Z Has data issue: false hasContentIssue false
  • English
  • Français

Visualising alternating geometric series

Published online by Cambridge University Press:  20 June 2025

Michael Waters  and
Ritam Sinha
Michael Waters
Affiliation:
Department of Mathematics and Statistics, Northern Kentucky University, Highland Heights, KY 41099, USA e-mail: watersm1@nku.edu
Ritam Sinha
Affiliation:
Ramakrishna Mission Vivekananda Centenary College, Rahara, India e-mail: ritamsinha23@gmail.com
Get access Rights & Permissions [Opens in a new window]

Extract

When first learning about geometric series, students often wonder why these series are termed 'geometric'. The geometry of some geometric series is readily apparent for some common series such as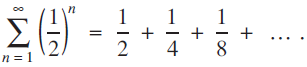

$$\sum\limits_{n = 1}^\infty{\left( {\frac{1}{2}} \right)}^n = \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + ...{\text{ }}.$$

Type
Articles
Information
The Mathematical Gazette , Volume 109 , Issue 575 , July 2025 , pp. 223 - 230
Check for updates
Copyright
© The Authors, 2025 Published by Cambridge University Press on behalf of The Mathematical Association

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Plaza, A., Sum of an alternating geometric series via self-similarity. American Mathematical Monthly, 129(4) (2022) p. 380.CrossRefGoogle Scholar
Chakraborty, B., Sum of a geometric series via the integral $\int_1^r {\frac{1}{x}dx}$ . American Mathematical Monthly, 130 (8) (2023) p. 764.CrossRefGoogle Scholar
Sinha, R., Visualizing an alternating series. Ohio Journal of School Mathematics, 92 (2022) pp. 57–61. https://library.osu.edu/ojs/index.php/OJSM/article/view/9282/7772 Google Scholar
Rep-tile,Wikipedia, accessed November 2024 at https://en.wikipedia.org/wiki/Rep-tile Google Scholar