No CrossRef data available.
Article contents
The three centroids of a polygonal lamina
In memory of Nick Lord
Published online by Cambridge University Press: 20 June 2025
Extract
The centre of mass of a plane, uniform, lamina in the shape of a regular n-gon coincides with the centre of mass of n unit masses, one at each of its vertices. As many n-gons fail to have this property it is remarkable that all triangular laminas, whether regular (i.e. equilateral) or not, do have this property. Here we discuss this difference and we assume throughout that each lamina has unit density (so, disregarding units, its mass is the same as its area). We shall refer to the centre of mass 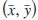 of the lamina as its centroid, and the centre of mass
of the lamina as its centroid, and the centre of mass 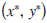 of unit point masses, one at each vertex, as its vertex-centroid. Also, we shall say that a polgonal lamina is vertex-equivalent if its centroid coincides with its vertex-centroid, i.e. if, and only if,
of unit point masses, one at each vertex, as its vertex-centroid. Also, we shall say that a polgonal lamina is vertex-equivalent if its centroid coincides with its vertex-centroid, i.e. if, and only if, 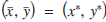 .
.
Information
- Type
- Articles
- Information
- Copyright
- © The Authors, 2025 Published by Cambridge University Press on behalf of The Mathematical Association


