It is well known that the real geometric series 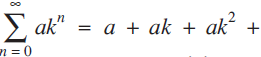${\sum\limits_{n = 0}^\infty{a{k^n} = a + ak + a{k^2} + }}$ … converges to a definite sum if the common ratio, k, is such that |k| < 1, the sum being 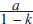${a}\over{1-k}$. For example, if a = 1 and 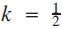${k ={{1}\over{2}}}$ we obtain the series 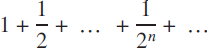${{1} + {{1}\over{2}} + ... + {{1}\over{2}^n} + ...}$, whose partial sums are 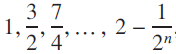${{1}, {{3}\over{2}}, {{7}\over{4}}, ..., 2 -{{1}\over{2}^n}}$, …, and these are clearly approaching the value 2 as n becomes larger and larger. As n → ∞, 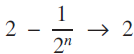${2} - {{1}\over{2}^n}{\unicode{x2192}} \,\,2$, in agreement with the formula 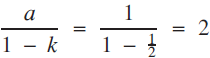${{a}\over{1-k}} {=} {{1}\over{1}-{1\over2}}=2$.