No CrossRef data available.
Article contents
Quotient polynomials with positive coefficients
Published online by Cambridge University Press: 23 January 2015
Extract
In a recent paper [1] Michael Hirschhorn and the present author had to prove that the polynomial
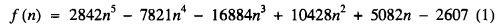
is positive for all integers n ≥ 4. We did so by writing down the identity
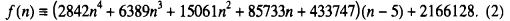
Since all the coefficients of the quotient polynomial are positive as well as the remainder, this shows by inspection that f(n) > 0 for n ≥ 5 and computing f(4) = 12025 completes the proof. This example illustrates a useful and efficient method for proving that polynomials have strictly positive values for all real numbers exceeding a given one. We leamed this method from a paper by Chen [2], (see [3] and the references cited there), and we have subsequently used it in our own researches [1,4].
We also conjectured in [1] that the theoretical basis of the method is a true theorem and the present paper is dedicated to proving this conjecture.
Theorem 1: Let f(x) be a polynomial with real coefficients whose leading coefficient is positive and with at least one positive root x = a. Then there exists an x = b ≥ a such that
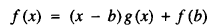
where f(b), and all the coefficients of the quotient polynomial g(x), are non-negative.
Information
- Type
- Articles
- Information
- Copyright
- Copyright © Mathematical Association 2014

