No CrossRef data available.
Article contents
The probabilistic nature of Wallis's formula
Published online by Cambridge University Press: 23 January 2015
Extract
The beautiful representation of π by Wallis's product formula has attracted many authors who have given a variety of proofs (see [1, 2, 3, 4, 5, 6, 7]). The purpose of this note is to revisit some elementary derivations with a focus on probabilistic/statistical flavours of this formula. The famous Wallis's product formula for 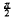 is given by
is given by
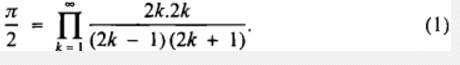
There are a number proofs available for this formula scattered in the literature. Here we will concentrate on the probabilistic nature of this formula.
Information
- Type
- Articles
- Information
- Copyright
- Copyright © The Mathematical Association 2012
References
1.
Boros, G. and Moll, V., Irresistible integrals, symbolics, analysis and experiments in the evaluation of integrals, Cambridge University Press, (2004).CrossRefGoogle Scholar
5.
Miller, Steven J., A probabilistic proof of Wallis's formula for π, Amer. Math. Monthly
115 no. 8 (2008) pp. 740–745.CrossRefGoogle Scholar
6.
Vito, Lampret, Wallis sequence estimated through the Euler-Maclaurin formula, Austral. Math. Soc. Gaz.
31, no. 5 (2004) pp. 328–339.Google Scholar
8.
Levrie, Paul and Daems, Walter, Evaluating the probability integral using Wallis's product formula for π, Amer. Math. Monthly
116, no. 6 (2009) pp. 538–541.CrossRefGoogle Scholar

