No CrossRef data available.
Article contents
A New Numerical Method of Solving a Space Triangle
Published online by Cambridge University Press: 03 November 2016
Extract
Applying this method we evaluate (see Fig. 1) the projections of the vector 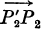 (the height at P 2 of the given triangle), and also the co-ordinates of the point
(the height at P 2 of the given triangle), and also the co-ordinates of the point 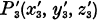 in which the perpendicular form
in which the perpendicular form
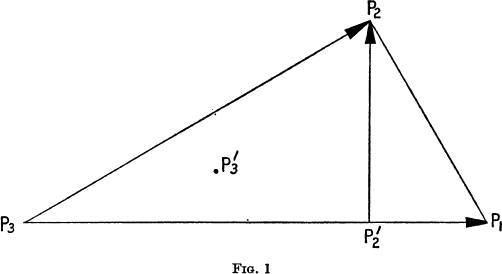
the origin meets the plane of the triangle. In this way, as will be shown, we find immediately the co-ordinates of the perpendicular projection 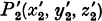 of the given point P 2(x 2, y 2, z 2) on the straight line passing through P 3 and P 1, and also the equation of the plane of the triangle.
of the given point P 2(x 2, y 2, z 2) on the straight line passing through P 3 and P 1, and also the equation of the plane of the triangle.
Information
- Type
- Other
- Information
- Copyright
- Copyright © Mathematical Association 1965

