Article contents
The morphology of 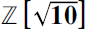 ${\mathbb{Z}}\sqrt {{\rm{[10]}}} $
${\mathbb{Z}}\sqrt {{\rm{[10]}}} $
Published online by Cambridge University Press: 21 October 2019
Extract
What are the units, irreducibles, and primes of the ring 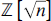 ${\mathbb{Z}}\sqrt n $, the set of all numbers
${\mathbb{Z}}\sqrt n $, the set of all numbers 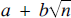 $a + b\sqrt n $where a and b are integers and n is a fixed positive square-free integer? In the ring
$a + b\sqrt n $where a and b are integers and n is a fixed positive square-free integer? In the ring 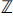 ${\mathbb{Z}}$, primes and irreducibles are synonymous and its units are ±1.
${\mathbb{Z}}$, primes and irreducibles are synonymous and its units are ±1.  ${\mathbb{Z}}\sqrt n $ is wilder, and our modest goal here is to catalogue all such numbers for
${\mathbb{Z}}\sqrt n $ is wilder, and our modest goal here is to catalogue all such numbers for 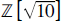 ${\mathbb{Z}}\sqrt {{\rm{[10]}}} $, where a and b range from 0 to 10; the result appears in Figure 1. Here are a few teasers that may induce a reader to read on:
${\mathbb{Z}}\sqrt {{\rm{[10]}}} $, where a and b range from 0 to 10; the result appears in Figure 1. Here are a few teasers that may induce a reader to read on: 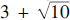 $3 + \sqrt {10} $ is a unit; 2, 3, 5, and 7 are irreducibles, but not 31; and 7 is the least positive integer that is prime in both
$3 + \sqrt {10} $ is a unit; 2, 3, 5, and 7 are irreducibles, but not 31; and 7 is the least positive integer that is prime in both 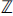 ${\mathbb{Z}}$ and
${\mathbb{Z}}$ and 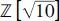 ${\mathbb{Z}}\sqrt {{\rm{[10]}}} $.
${\mathbb{Z}}\sqrt {{\rm{[10]}}} $.
Information
- Type
- Articles
- Information
- Copyright
- © Mathematical Association 2019
References
- 1
- Cited by

