Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Nickalls, R. W. D.
2000.
84.34 The quadratic formula is a particular case.
The Mathematical Gazette,
Vol. 84,
Issue. 500,
p.
276.
Panayi, A. P.
Diaz, A. R.
and
Schock, H. J.
2009.
On the optimization of piston skirt profiles using a pseudo-adaptive response surface method.
Structural and Multidisciplinary Optimization,
Vol. 38,
Issue. 3,
p.
317.
van Rensburg, E J Janse
2011.
Adsorption of pulled directed paths in a slanted boundary.
Journal of Physics A: Mathematical and Theoretical,
Vol. 44,
Issue. 32,
p.
325001.
Mason, John
2011.
Phenomenology of example construction.
ZDM,
Vol. 43,
Issue. 2,
p.
195.
Cao, Wensheng
and
Gongopadhyay, Krishnendu
2012.
Algebraic characterization of isometries of the complex and the quaternionic hyperbolic planes.
Geometriae Dedicata,
Vol. 157,
Issue. 1,
p.
23.
De Simone, Pasquale
2012.
Head embedment in Broms pile lateral capacity theory for cohesionless soils.
Computers and Geotechnics,
Vol. 43,
Issue. ,
p.
51.
Gongopadhyay, Krishnendu
and
Parsad, Shiv
2013.
Classification of quaternionic hyperbolic isometries.
Conformal Geometry and Dynamics of the American Mathematical Society,
Vol. 17,
Issue. 7,
p.
68.
Pereira, Jorge Vitório
and
Pirio, Luc
2015.
An Invitation to Web Geometry.
p.
1.
Clamond, Didier
Dutykh, Denys
and
Galligo, André
2016.
Algebraic method for constructing singular steady solitary waves: a case study.
Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 472,
Issue. 2191,
p.
20160194.
Pauwelyn, P. J.
and
Guerry, M. A.
2022.
Perturbations of non-diagonalizable stochastic matrices with preservation of spectral properties.
Linear and Multilinear Algebra,
Vol. 70,
Issue. 20,
p.
5115.
Santana, Paulo
2024.
On the structural instability of non-hyperbolic limit cycles on planar polynomial vector fields.
São Paulo Journal of Mathematical Sciences,
Vol. 18,
Issue. 2,
p.
1605.
Bastos, Jefferson
Buzzi, Claudio
and
Santana, Paulo
2024.
On structural stability of evolutionary stable strategies.
Journal of Differential Equations,
Vol. 389,
Issue. ,
p.
190.
Marques, Gil
and
Gama, Sílvio
2025.
Geometric Characterization of Atmospheric Islands Formed by Two Point Vortices.
Axioms,
Vol. 14,
Issue. 4,
p.
272.
Salizzoni, Giulio
Ouhamma, Reda
and
Kamgarpour, Maryam
2025.
Nash equilibria in scalar discrete-time linear quadratic games.
p.
2416.

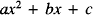 to have two equal roots, i.e. to have a repeated root, is that its discriminant
to have two equal roots, i.e. to have a repeated root, is that its discriminant 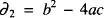 should be zero. We should remark, at the outset, that we are concerned only with ordinary polynomials whose coefficients are complex numbers. Indeed, little is lost if a reader assumes that all our polynomials are real, i.e. have real numbers for all their coefficients, though their complex roots must be considered as well as their real ones.
should be zero. We should remark, at the outset, that we are concerned only with ordinary polynomials whose coefficients are complex numbers. Indeed, little is lost if a reader assumes that all our polynomials are real, i.e. have real numbers for all their coefficients, though their complex roots must be considered as well as their real ones.