Article contents
Extract
1. Let f(x) be a real function of a real variable x. The meanings of 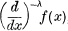 when λ is a positive integer, a negative integer and zero, are well known. In the first case,
when λ is a positive integer, a negative integer and zero, are well known. In the first case, 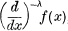 denotes the λth integral of f(x) with respect to x, with an arbitrary lower limit of integration. In the second case,
denotes the λth integral of f(x) with respect to x, with an arbitrary lower limit of integration. In the second case, 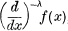 stands for the (−λ)th differential coefficient of f(x) with respect to x. Lastly, when λ = 0,
stands for the (−λ)th differential coefficient of f(x) with respect to x. Lastly, when λ = 0, 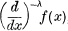 means f(x).
means f(x).
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Mathematical Association 1936
References
Page no 88 note * Leibnitz, Opera, ed. Dutens, 3, Commercium Phiols. et Math., p. 105(1695).
Page no 88 note † Liouville, , Journal de l’Ecole Polytechnic, 13, pp.1–186 (1832)Google Scholar.
Page no 88 note ‡ Riemann, Gesammelte Werke, pp. 331-344 (1876).
Page no 88 note § Ferrar, , Proc. Edin. Math. Soc., 48, pp. 92–105 (1927).CrossRefGoogle Scholar
Page no 89 note * Fabian, , Philosophical Magazine, ser. 7, vol. 20, pp. 781–789 (1935)Google Scholar. The index laws and the Riemann series are dealt with here.
- 2
- Cited by

