Hostname: page-component-5b777bbd6c-sbgtn Total loading time: 0 Render date: 2025-06-21T16:25:18.543Z Has data issue: false hasContentIssue false
  • English
  • Français

The Euler numbers and their last digits

Published online by Cambridge University Press:  20 June 2025

Warren P. Johnson
Warren P. Johnson*
Affiliation:
Connecticut College, 270 Mohegan Avenue, New London, CT 06320 USA e-mail: wpjoh@conncoll.edu
Get access Rights & Permissions [Opens in a new window]

Extract

The Euler numbers are the coefficients En in the expansion

(1)

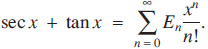
Since sec x is an even function and tan x an odd one, this decouples into

(2)

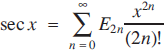
and

(3)

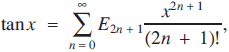
where all three series converge if 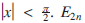and E2n + 1 are sometimes called the secant numbers (or secant coefficients) and tangent numbers (or tangent coefficients) respectively.

Type
Articles
Information
The Mathematical Gazette , Volume 109 , Issue 575 , July 2025 , pp. 259 - 264
Check for updates
Copyright
© The Authors, 2025 Published by Cambridge University Press on behalf of The Mathematical Association

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Euler, Leonhard, Institutiones calculi differentialis, Academiae Imperialis Scientiarum, 1755; Opera Omnia, 1st series, vol. 10, B. G. Teubner, Leipzig, 1913.Google Scholar
Euler, Leonhard, De seriebus quibusdam considerationes, Commentarii academiae scientiarum Petropolitanae 12 (1740), 1750, pp. 53–96; Opera Omnia, 1st series, vol. 14, B. G. Teubner, Leipzig (1925) pp. 407-462.Google Scholar
Forder, H. G., Euler Numbers, Math. Gaz. 14 (October 1928) p. 233.Google Scholar
André, Désiré, Développements de sec x et de tang x, Comptes Rendus hebdomadaires des scéances de l’Academie des sciences 88 (1879), pp. 965–967.Google Scholar
André, Désiré, Sur les permutations alternées, Journal de mathématiques pures et appliquées, 7 (1881) pp. 167–184.Google Scholar
Stanley, Richard P., A survey of alternating permutations (2009), accessed November 2024 at https://arXiv.org/pdf/0912.4240 Google Scholar
Carlitz, Leonard, Enumeration of up-down permutations by number of rises, Pacific Journal of Mathematics 45 (1973) pp. 49–59.CrossRefGoogle Scholar
Carlitz, Leonard, Permutations and sequences, Advances in mathematics 14 (1974) pp. 92–120.CrossRefGoogle Scholar
Carlitz, Leonard, Permutations, sequences, and special functions, SIAM Review 17 (1975) pp. 298–322.CrossRefGoogle Scholar
Carlitz, Leonard and Scoville, Richard, Enumeration of up-down permutations by upper records, Monatshefte für Mathematik 79 (1975) pp. 3–12.CrossRefGoogle Scholar
Ferdinand Scherk, Heinrich, Mathematische Abhandlungen, G. Reimer, Berlin (1825).Google Scholar
Moritz Abraham Stern, Zur Theorie der Eulerschen Zahlen, Journal für die reine und angewandte Mathematik 79 (1875) pp. 67–98.Google Scholar
Glaisher, J. W. L., On Eulerian numbers (formulæ, residues, end-figures), with the values of the first twenty-seven, Quarterly Journal of Pure and Applied Mathematics 45 (1914) pp. 1–51.Google Scholar
He, Yuan and Liao, Qunying, Some congruences involving Euler numbers, Fibonacci Quarterly 46/47 (3) (August 2009) pp. 225–234.Google Scholar