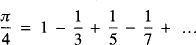Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Chien-Lih, Hwang
1997.
81.22 More Machin-type identities.
The Mathematical Gazette,
Vol. 81,
Issue. 490,
p.
120.
McGlynn, John E.
Singmaster, David
Wetherfield, Michael
Chien-Lih, Hwang
and
MacHale, Des
1997.
Correspondence.
The Mathematical Gazette,
Vol. 81,
Issue. 492,
p.
457.
Wetherfield, Michael
1997.
81.23 Machin revisited.
The Mathematical Gazette,
Vol. 81,
Issue. 490,
p.
121.
Chien-Lih, Hwang
2004.
88.38 Some observations on the method of arctangents for the calculation of π.
The Mathematical Gazette,
Vol. 88,
Issue. 512,
p.
270.
Calcut, Jack S.
2009.
Gaussian Integers and Arctangent Identities for π.
The American Mathematical Monthly,
Vol. 116,
Issue. 6,
p.
515.
Pla, Juan
2011.
Some remarks about a formula of Charles Dodgson.
The Mathematical Gazette,
Vol. 95,
Issue. 533,
p.
235.
Ruedas, Thomas
2017.
Globally smooth approximations for shock pressure decay in impacts.
Icarus,
Vol. 289,
Issue. ,
p.
22.
Balaji, Nikhil
Perifel, Sylvain
Shirmohammadi, Mahsa
and
Worrell, James
2021.
Cyclotomic Identity Testing and Applications.
p.
35.
Abrarov, Sanjar M.
Jagpal, Rajinder K.
Siddiqui, Rehan
and
Quine, Brendan M.
2021.
Algorithmic Determination of a Large Integer in the Two-Term Machin-like Formula for π.
Mathematics,
Vol. 9,
Issue. 17,
p.
2162.
Gasull, Armengol
Luca, Florian
and
Varona, Juan L.
2023.
Three essays on Machin’s type formulas.
Indagationes Mathematicae,
Vol. 34,
Issue. 6,
p.
1373.
Abrarov, Sanjar M.
Siddiqui, Rehan
Jagpal, Rajinder Kumar
and
Quine, Brendan M.
2024.
An Iterative Method for Computing π by Argument Reduction of the Tangent Function.
Mathematical and Computational Applications,
Vol. 29,
Issue. 2,
p.
17.

 , the simplest, and most slowly convergent, series of this kind is
, the simplest, and most slowly convergent, series of this kind is