Hostname: page-component-5b777bbd6c-v4w92 Total loading time: 0 Render date: 2025-06-21T14:31:15.918Z Has data issue: false hasContentIssue false
  • English
  • Français

A caution (or two) regarding mathematical expectation

Published online by Cambridge University Press:  20 June 2025

Leonard M. Wapner
Leonard M. Wapner*
Affiliation:
Division of Mathematical Sciences, El Camino College, Torrance, CA 90506, USA e-mail: lwapner@elcamino.edu
Get access Rights & Permissions [Opens in a new window]

Extract

Computing mathematical expectation for an experiment involving a finite number of numerical outcomes is straightforward. Let X denote the random variable having n possible values x1, x2, x3,…, xn. Letting pk denote the probability of xk, the expected value of X is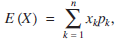

$$E\,(X)\, = \,\sum\limits_{k\, = \,1}^n {{x_k}{p_k}} ,$$

which can be interpreted as a weighted average of all xk, where the weight of each outcome is represented by its probability. But caution is required when interpreting the sum if there are infinitely many outcomes and the series fails to converge absolutely.

Type
Articles
Information
The Mathematical Gazette , Volume 109 , Issue 575 , July 2025 , pp. 247 - 252
Check for updates
Copyright
© The Authors, 2025 Published by Cambridge University Press on behalf of The Mathematical Association

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Gale, D., Tracking the automatic ant and other mathematical explorations, Springer-Verlag (1998).CrossRefGoogle Scholar
Hacking, I., Strange expectations, Philosophy of Science, 47(4) (1980) pp. 562-567.CrossRefGoogle Scholar
Nathan, A., False expectations, Philosophy of Science, 51(1) (1984) pp. 128-136.CrossRefGoogle Scholar
Kraitchik, M., Mathematical recreations (2nd edn.), Dover (1953).Google Scholar
Gardner, M., Aha! gotcha: paradoxes to puzzle and delight, W. H. Freeman and Company (1982).Google Scholar
Wapner, L., Unexpected expectations: the curiosities of a mathematical crystal ball, CRC Press (2012).CrossRefGoogle Scholar
Wagner, C. H., Simpson’s paradox in real life, The American Statistician, 36 (1982) pp. 46–48.CrossRefGoogle Scholar
Taleb, N. N., The black swan: the impact of the highly improbable (2nd edn.), Random House (2010).Google Scholar