A very simple way of generating a sequence is to take two starting values, a 1 and a 2, and construct a 3 as their arithmetic mean, a 4 as the mean of a 2 and a 3 and so on. This sequence always converges to the limit 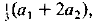and seems to be fairly widely known as a topic for investigation in schools and colleges. It can immediately be generalised to the case of k starting values, and this forms a good subject for investigation using a micro-computer. It seems likely that such a simple set-up has arisen independently many times. One emergence occurred about ten years ago at a conference of the Association of Teachers of Mathematics, where the originator introduced it under the fictitious name ‘Littov sequences’. It has recently resurfaced at a Department of Education and Science conference.