A series of consecutive odd numbers has interesting properties useful for classroom investigation [1]. This Article was inspired by the series of fractions for 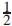${{1}\over{2}}$ using only sums of consecutive odd numbers

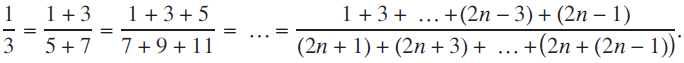$$\frac{1}{3} = \frac{{1 + 3}}{{5 + 7}} = \frac{{1 + 3 + 5}}{{7 + 9 + 11}} = {\text{ }} \ldots {\text{ }} = \frac{{1 + 3 + {\text{ }} \ldots {\text{ }} + (2n - 3) + (2n - 1)}}{{(2n + 1) + (2n + 3) + {\text{ }} \ldots {\text{ }} + (2n + (2n - 1))}}.$$