Hostname: page-component-5b777bbd6c-6lqsf Total loading time: 0 Render date: 2025-06-21T22:19:36.701Z Has data issue: false hasContentIssue false
  • English
  • Français

The most concise recurrence formula for the sums of integer powers

Published online by Cambridge University Press:  20 June 2025

José Luis Cereceda
José Luis Cereceda*
Affiliation:
C/La Fragua 11, Bajo A, Collado Villalba, 28400 Madrid, Spain e-mail: jl.cereceda@movistar.es
Get access Rights & Permissions [Opens in a new window]

Extract

For integers n, 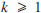, let Sk (n) denote the power sum 1k + 2k +… + nk, with S0 (n) = n. As is well known, Sk (n) can be represented by a polynomial in n of degree k + 1 with constant term equal to zero, i.e. 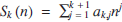${S_k}\,(n)\, = \,\mathop \sum \nolimits_{j\, = \,1}^{k\, + \,1} \,{a_{k,j}}{n^j}$, for certain rational coefficients ak,j. In 1973, in the popular science magazine Kvant*, appeared an article by Vladimir Abramovich [1] in which, among other things, the author derived the following minimal recurrence relation which expresses in a very compact way the connection between the power sums Sk (n) and Sk-1 (n):

(1)

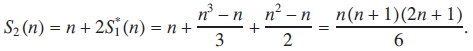
where the polynomial 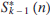$S_{k\, - \,1}^*\,(n)$ is constructed by replacing in Sk-1 (n) the term nj with the expression 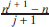${{{n^{j + 1}} - n} \over {j + 1}}$ for each j = 1, 2, … , k. Note that 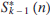$S_{k\, - \,1}^*\,(n)$ has degree k + 1, as it should be.

Type
Articles
Information
The Mathematical Gazette , Volume 109 , Issue 575 , July 2025 , pp. 253 - 258
Check for updates
Copyright
© The Authors, 2025 Published by Cambridge University Press on behalf of The Mathematical Association

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Abramovich, V., Sums of equal powers of natural numbers, Kvant 5 (1973) pp. 22-25 (in Russian). This article was later translated and adapted with permission in Crux Mathematicorum 40(6) (2014) pp. 248–252.Google Scholar
Shevelev, V. S., A short proof of a known relation for consecutive power sums, arXiv preprint (2007).Google Scholar
Bloom, D. M., An old algorithm for the sums of integer powers, Math. Mag. 66(5) (1993) pp. 304–305.CrossRefGoogle Scholar
Owens, R. W., Sums of powers of integers, Math. Mag. 65(1) (1992) pp. 38–40.CrossRefGoogle Scholar
Carchidi, M., Two simple recursive formulas for summing 1k + 2k +… + n k , Coll. Math. J. 18(5) (1987) pp. 406–409.Google Scholar
Doucet, J. and Saleh-Jahromi, A., Sums of powers of integers, Research paper in Proceedings of the Louisiana-Mississippi Section of the Mathematical Association of America (Spring 2002).Google Scholar
Torabi-Dashti, M., Faulhaber’s triangle, Coll. Math. J. 42(2) (2011) pp. 9697.CrossRefGoogle Scholar
Sherwood, H., Sums of powers of integers and Bernoulli numbers, Math. Gaz. 54 (October 1970) pp. 272–274.CrossRefGoogle Scholar
Coen, L. E. S., Sums of powers and the Bernoulli numbers, Master Thesis Eastern Illinois University (1996) accessed November 2024 at https://thekeep.eiu.edu/theses/1896/ Google Scholar
Costa, S., Geometry of the sums of consecutive integer powers, Math. Gaz. 92 (November 2008) pp. 516–522.CrossRefGoogle Scholar
Edwards, H. M., Fermat’s last theorem: A genetic introduction to algebraic number theory, Springer-Verlag (1977) pp. 229–230.CrossRefGoogle Scholar
Budin, M. A. and Cantor, A. J., Simplified computation of sums of powers of integers, IEEE Trans. Syst. Man Cybern., SMC-2(2) (1972) pp. 284–285 accessed November 2024 at https://doi.org/10.1109/TSMC.1972.4309107 Google Scholar
Wu, D. W., Bernoulli numbers and sums of powers, Int. J. Math. Educ. Sci. Technol. 32(3) (2001) pp. 440–443.CrossRefGoogle Scholar
Booth, R. and Nguyen, H. D., Bernoulli polynomials and Pascal’s square, Fibonacci Quart. 46/47(1) (February 2008/2009) pp. 38–47.Google Scholar
Qi, F. and Guo, B.-N., Some determinantal expressions and recurrence relations of the Bernoulli polynomials, Mathematics 4 (2016) Article number 65.CrossRefGoogle Scholar