Article contents
A cubic surface of revolution
Published online by Cambridge University Press: 23 January 2015
Extract
A well-known exercise in classical differential geometry [1, 2, 3] is to show that the set 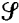 of all points (x, y, z) ∈ ℝ3 which satisfy the cubic equation
of all points (x, y, z) ∈ ℝ3 which satisfy the cubic equation

is a surface of revolution.
The standard proof ([2], [3, p. 11]), which, in principle, goes back to Lagrange [4] and Monge [5], is to verify that (1) satisfies the partial differential equation (here written as a determinant)

which characterises any surface of revolution F (x, y, z) = 0 whose axis of revolution has direction numbers (l, m, n) and goes through the point (a, b, c). This PDE, for its part, expresses the geometric property that the normal line through any point of 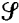 must intersect the axis of revolution (this is rather subtle; see [6]). All of this, though perfectly correct, seems complicated and rather sophisticated just to show that one can obtain
must intersect the axis of revolution (this is rather subtle; see [6]). All of this, though perfectly correct, seems complicated and rather sophisticated just to show that one can obtain 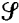 by rotating a suitable curve around a certain fixed line. Moreover, to carry out this proof one needs to know a priori just what this axis is, something not immediately clear from the statement of the problem. Nor does the solution give much of a clue as to which curve one rotates.
by rotating a suitable curve around a certain fixed line. Moreover, to carry out this proof one needs to know a priori just what this axis is, something not immediately clear from the statement of the problem. Nor does the solution give much of a clue as to which curve one rotates.
A search of the literature failed to turn up a treatment of the problem which differs significantly from that sketched above (although see [1]).
The polynomial (1) is quite famous and has been the object of numerous algebraical and number theoretical investigations. See the delightful and informative paper [7].
Information
- Type
- Articles
- Information
- Copyright
- Copyright © Mathematical Association 2014
References
- 1
- Cited by

