1. Introduction
Real business cycle (RBC) models and their modern versions in dynamic stochastic general equilibrium (DSGE) models have enjoyed a great deal of success since they were first introduced to the literature by Kydland and Prescott (Reference Kydland and Prescott1982). These models are the standard framework used by academics and policymakers to understand economic fluctuations and analyze the effects of monetary and fiscal policies on the macroeconomy. They typically feature rational optimizing agents and various sources of random disturbances to preferences, technology, government purchases, monetary policy rules, and/or international trade. Two notable disturbances, that are now considered standard, are shocks to neutral technology (NT) and shocks to investment-specific technology (IST). NT shocks make both labor and existing capital more productive. On the other hand, IST shocks have no impact on the productivity of old capital goods, but they make new capital goods more productive and less expensive.
Nonetheless, the modeling of these two types of technology in many DSGE models often varies greatly from a stationary process to an integrated smooth trend process, with each choice having different implications for the variations in economic activity and the analysis of macro variables. In this paper, we revisit the question of the specification of NT and IST via the lens of an unobserved components (UCs) model of the total factor productivity (TFP) and the relative price of investment (RPI). Specifically, the approach allows us to decompose a series into two unobserved components: one UC that reflects permanent or trend movements in the series, and the other that captures transitory movements in the series. In addition, based on the stock of evidence from Schmitt-Grohé and Uribè (Reference Schmitt-Grohé and Uribè2011), Benati (Reference Benati2013), Basu et al. (Reference Basu, Fernald and Oulton2003), Chen and Wemy (Reference Chen and Wemy2015), and other studies that appear to indicate that the two series are related in the long run, we specify that RPI and TFP share a common unobserved trend component. We label this component as general purpose technology (GPT), and we argue that it reflects spillover effects from innovations in information and communication technologies to aggregate productivity. As demonstrated in other studies, we contend that such an analysis of the time series properties of TFP and RPI must be the foundation for the choice of the stochastic processes of NT and IST in DSGE models.
The UC framework offers ample flexibility and greater benefits. First, our framework nests all competing theories of the univariate and bivariate properties of RPI and TFP. In fact, the framework incorporates Schmitt-Grohé and Uribè (Reference Schmitt-Grohé and Uribè2011)’s result of co-integration and Benati (Reference Benati2013)’s findings of the long-run positive comovement as special cases. In that sense, we are able to evaluate the validity of all the proposed specifications of NT and IST in the DSGE literature. Furthermore, the UC structure yields a quantitative estimate, in addition to the qualitative measure in Benati (Reference Benati2013), of potential scale differences between the trends of RPI and TFP. Last, but not least, it is grounded on economic theory. In particular, we demonstrate that our UC framework may be derived from the neoclassical growth model used by studies in the growth accounting literature, for example, Greenwood et al. (Reference Greenwood, Hercowitz and Huffman1997a, Reference Greenwood, Hercowitz and Per1997b), Oulton (Reference Oulton2007), and Greenwood and Krusell (Reference Greenwood and Krusell2007), to investigate the contribution of embodiment in the growth of aggregate productivity. As such, we may easily interpret the idiosyncratic UC of RPI and TFP, and their potential interaction from the lenses of a well-defined economic structure.
Using the time series of the logarithm of (the inverse of) RPI and TFP from
![]() $1959.II$
to
$1959.II$
to
![]() $2019.II$
in the USA, we estimate our UC model through Markov chain Monte Carlo methods developed by Chan and Jeliazkov (Reference Chan and Jeliazkov2009) and Grant and Chan (Reference Grant and Chan2017). A novel feature of this approach is that it builds upon the band and sparse matrix algorithms for state space models, which are shown to be more efficient than the conventional Kalman filter-based algorithms. Two points emerge from our estimation results.
$2019.II$
in the USA, we estimate our UC model through Markov chain Monte Carlo methods developed by Chan and Jeliazkov (Reference Chan and Jeliazkov2009) and Grant and Chan (Reference Grant and Chan2017). A novel feature of this approach is that it builds upon the band and sparse matrix algorithms for state space models, which are shown to be more efficient than the conventional Kalman filter-based algorithms. Two points emerge from our estimation results.
First, our findings indicate that the idiosyncratic trend component in RPI and TFP is better captured by a differenced first-order autoregressive, ARIMA(1,1,0), process; a result which suggests that NT and IST should each be modeled as following an ARIMA(1,1,0) process. While several papers like Justiniano et al. (Reference Justiniano, Primiceri and Tambalotti2011a, Reference Justiniano, Primiceri and Tambalotti2011b), Schmitt-Grohé and Uribè (Reference Schmitt-Grohé and Uribè2011), and Kaihatsu and Kurozumi (Reference Kaihatsu and Kurozumi2014) adopt an ARIMA(1,1,0) specification, other notable studies such as Smets and Wouters (Reference Smets and Wouters2007) and Fisher (Reference Fisher2006) impose either a trend stationary ARMA(1,0) process or an integrated ARIMA(0,1,0) process, respectively. Through our exploration of the literature, we find that this disconnected practice is complicated by two important facts. The first fact is that it is not easy to establish whether highly persistent macro data are trend stationary or difference stationary in finite sample. Since the models are expected to fit the data along this dimension, researchers typically take a stand on the specification of the trend in DSGE models by arbitrarily building into these models stationary or nonstationary components of NT and IST. Then, the series are transformed accordingly in the same fashion prior to the estimation of the parameters of the models. However, several studies demonstrate that this approach may create various issues such as generating spurious cycles and correlations in the filtered series, and/or altering the persistence and the volatility of the original series. The second fact, which is closely related to the first, is that DSGE models must rely on impulse dynamics to match the periodicity of output as such models have weak amplification mechanisms. In DSGE models, periodicity is typically measured by the autocorrelation function of output. Many studies document that output growth is positively correlated over short horizons. Consequently, if technology follows a differenced first-order autoregressive, ARIMA(1,1,0), process, the model will approximately mimic the dynamics of output growth in the data. Therefore, our results serve to reduce idiosyncratic trend misspecification which may lead to erroneous conclusions about the dynamics of macroeconomic variables.
The second point is that while the idiosyncratic trend component in each (the inverse of RPI and TFP) is not common to both series, it appears that the variables share a common stochastic trend component which captures a positive long-run covariation between the series. We argue that the common stochastic trend component is a reflection of GPT progress from innovations in information and communications technologies. In fact, using industry-level and aggregate-level data, several studies, such as Cummins and Violante (Reference Cummins and Violante2002), Basu et al. (Reference Basu, Fernald and Oulton2003), and Jorgenson et al. (Reference Jorgenson, Ho, Samuels and Stiroh2007), document that improvements in information communication technologies contributed to productivity growth in the 1990s and the 2000s in essentially every industry in the USA. Through our results, we are also able to confirm that changes in the trend of RPI have lasting impact on the long-run developments of TFP. In addition, errors associated with the misspecification of common trend between NT and IST may bias conclusions about the source of business cycle fluctuations in macroeconomic variables. For instance, Schmitt-Grohé and Uribè (Reference Schmitt-Grohé and Uribè2011) shows that when NT and IST are co-integrated, then the shocks to the common stochastic trend become the major source of fluctuations of output, investment, and hours. This challenges results in several studies which demonstrate that exogenous disturbances in either NT or IST, may individually, account for the majority of the business cycle variability in economic variables. Therefore, our results suggest that researchers might need to modify DSGE models to consider the possibility of the existence of this long-run relationship observed in the data and its potential effect on fluctuations.
2. The model
Fundamentally, there are multiple potential representations of the relationship between the trend components and the transitory components in RPI and TFP. We adopt the UC approach which stipulates that RPI and TFP can each be represented as the sum of a permanent component, an idiosyncratic component, and a transitory component in the following fashion:
where
![]() $z_{t}$
is the logarithm of RPI,
$z_{t}$
is the logarithm of RPI,
![]() $x_{t}$
is the logarithm of TFP,
$x_{t}$
is the logarithm of TFP,
![]() $\tau _{t}$
is the common trend component in RPI and TFP,
$\tau _{t}$
is the common trend component in RPI and TFP,
![]() $\tau _{x,t}$
is the idiosyncratic trend component in TFP, and
$\tau _{x,t}$
is the idiosyncratic trend component in TFP, and
![]() $c_{z,t}$
and
$c_{z,t}$
and
![]() $c_{x,t}$
are the corresponding idiosyncratic transitory components. The parameter
$c_{x,t}$
are the corresponding idiosyncratic transitory components. The parameter
![]() $\gamma$
captures the relationship between the trends in RPI and TFP.
$\gamma$
captures the relationship between the trends in RPI and TFP.
The first differences of the trend components are modeled as following stationary processes:
where
![]() $\eta _t\sim \mathcal{N}(0,\sigma _{\eta }^2)$
and
$\eta _t\sim \mathcal{N}(0,\sigma _{\eta }^2)$
and
![]() $\eta _{x,t}\sim \mathcal{N}(0,\sigma _{\eta _x}^2)$
are independent of each other at all leads and lags,
$\eta _{x,t}\sim \mathcal{N}(0,\sigma _{\eta _x}^2)$
are independent of each other at all leads and lags,
![]() $1(A)$
is the indicator function for the event A, and
$1(A)$
is the indicator function for the event A, and
![]() $T_{B}$
is the index corresponding to the time of the break at
$T_{B}$
is the index corresponding to the time of the break at
![]() $1982.I$
.
$1982.I$
.
Finally, following Morley et al. (Reference Morley, Nelson and Zivot2003) and Grant and Chan (Reference Grant and Chan2017), the transitory components are assumed to follow AR(2) processes:
where
![]() $\epsilon _{z,t}\sim \mathcal{N}(0,\sigma _{z}^2)$
,
$\epsilon _{z,t}\sim \mathcal{N}(0,\sigma _{z}^2)$
,
![]() $\epsilon _{x,t}\sim \mathcal{N}(0,\sigma _{x}^2)$
, and
$\epsilon _{x,t}\sim \mathcal{N}(0,\sigma _{x}^2)$
, and
![]() $corr(\varepsilon _{z,t},\varepsilon _{x,t}) = 0$
.Footnote
1
$corr(\varepsilon _{z,t},\varepsilon _{x,t}) = 0$
.Footnote
1
The presence of the common stochastic trend component in RPI and TFP captures the argument that innovations in information technologies are GPT, and they have been the main driver of the trend in RPI and a major source of the growth in productivity in the USA. Simply put, GPT can be defined as a new method that leads to fundamental changes in the production process of industries using it, and it is important enough to have a protracted aggregate impact on the economy. As discussed extensively in Jovanovic and Rousseau (Reference Jovanovic and Rousseau Peter2005), electrification and information technology (IT) are probably the most recent GPTs so far. In fact, using industry-level data, Cummins and Violante (Reference Cummins and Violante2002) and Basu et al. (Reference Basu, Fernald and Oulton2003) find that improvements in information communication technologies contributed to productivity growth in the 1990s in essentially every industry in the USA. Moreover, Jorgenson et al. (Reference Jorgenson, Ho, Samuels and Stiroh2007) show that much of the TFP gain in the USA in the 2000s originated in industries that are the most intensive users of IT. Specifically, the authors look at the contribution to the growth rate of value-added and aggregate TFP in the USA in 85 industries. They find that the four IT-producing industries (computer and office equipment, communication equipment, electronic components, and computer services) accounted for nearly all of the acceleration of aggregate TFP in 1995–2000. Furthermore, IT-using industries, which engaged in great IT investment in the period 1995–2000, picked up the momentum and contributed almost half of the aggregate acceleration in 2000–2005. Overall, the authors assert that IT-related industries made significant contributions to the growth rate of TFP in the period 1960–2005. Similarly, Gordon (Reference Gordon1990) and Cummins and Violante (Reference Cummins and Violante2002) have argued that technological progress in areas such as equipment and software have contributed to a faster rate of decline in RPI, a fact that has also been documented in Fisher (Reference Fisher2006) and Justiniano et al. (Reference Justiniano, Primiceri and Tambalotti2011a, Reference Justiniano, Primiceri and Tambalotti2011b).
A complementary interpretation of the framework originates from the growth accounting literature associated with the relative importance of embodiment in the growth of technology. In particular, Greenwood et al. (Reference Greenwood, Hercowitz and Huffman1997a, Reference Greenwood, Hercowitz and Per1997b), Greenwood and Krusell (Reference Greenwood and Krusell2007), and Oulton (Reference Oulton2007) show that the nonstationary component in TFP is a combination of the trend in NT and the trend in IST. In that case, we may interpret the common component,
![]() $\tau _{t}$
, as the trend in IST,
$\tau _{t}$
, as the trend in IST,
![]() $\tau _{x,t}$
as the trend in NT, and the parameter
$\tau _{x,t}$
as the trend in NT, and the parameter
![]() $\gamma$
as the current price share of investment in the value of output. In Appendix A.1, we show that our UC framework may be derived from a simple neoclassical growth model.
$\gamma$
as the current price share of investment in the value of output. In Appendix A.1, we show that our UC framework may be derived from a simple neoclassical growth model.
Furthermore, this UC framework offers more flexibility as it nests all the univariate and bivariate specifications of NT and IST in the literature. Specifically, let us consider the following cases:
-
1. If
 $\gamma = 0$
, then trends in RPI and TFP are independent of each other, and this amounts to the specifications adopted in Justiniano et al. (Reference Justiniano, Primiceri and Tambalotti2011a, Reference Justiniano, Primiceri and Tambalotti2011b) and Kaihatsu and Kurozumi (Reference Kaihatsu and Kurozumi2014).
$\gamma = 0$
, then trends in RPI and TFP are independent of each other, and this amounts to the specifications adopted in Justiniano et al. (Reference Justiniano, Primiceri and Tambalotti2011a, Reference Justiniano, Primiceri and Tambalotti2011b) and Kaihatsu and Kurozumi (Reference Kaihatsu and Kurozumi2014). -
2. If
 $\gamma = 0$
,
$\gamma = 0$
,
 $\varphi _{\mu } = 0$
, and
$\varphi _{\mu } = 0$
, and
 $\varphi _{\mu _{x}} = 0$
, then the trend components follow a random walk plus drift, and the resulting specification is equivalent to the assumptions found in Fisher (Reference Fisher2006).
$\varphi _{\mu _{x}} = 0$
, then the trend components follow a random walk plus drift, and the resulting specification is equivalent to the assumptions found in Fisher (Reference Fisher2006). -
3. If we pre-multiply equation (1) by
 $\gamma$
, and subtract the result from equation (2), we obtain(7)where
$\gamma$
, and subtract the result from equation (2), we obtain(7)where \begin{equation} x_{t} - \gamma z_{t} = \tau _{x,t} + c_{xz,t} \end{equation}
\begin{equation} x_{t} - \gamma z_{t} = \tau _{x,t} + c_{xz,t} \end{equation}
 $c_{xz,t} = c_{x,t} - \gamma c_{z,t}$
.
$c_{xz,t} = c_{x,t} - \gamma c_{z,t}$
.-
(a) If
 $\gamma \neq 0$
,
$\gamma \neq 0$
,
 $\varphi _{\mu _{x}} = 0$
, and
$\varphi _{\mu _{x}} = 0$
, and
 $\sigma _{\eta _{x}} = 0$
, then RPI and TFP are co-integrated, with co-integrating vector
$\sigma _{\eta _{x}} = 0$
, then RPI and TFP are co-integrated, with co-integrating vector
 $(-\gamma, 1)$
, as argued in Schmitt-Grohé and Uribè (Reference Schmitt-Grohé and Uribè2011).
$(-\gamma, 1)$
, as argued in Schmitt-Grohé and Uribè (Reference Schmitt-Grohé and Uribè2011). -
(b) If, in addition,
 $\zeta _{x} \neq 0$
, then
$\zeta _{x} \neq 0$
, then
 $\tau _{x,t}$
is a linear deterministic trend, and RPI and TFP are co-integrated around a linear deterministic trend.
$\tau _{x,t}$
is a linear deterministic trend, and RPI and TFP are co-integrated around a linear deterministic trend. -
(c) If, otherwise,
 $\zeta _{x} = 0$
, the RPI and TFP are co-integrated around a constant term.
$\zeta _{x} = 0$
, the RPI and TFP are co-integrated around a constant term.
-
-
4. If
 $\gamma \gt 0$
(
$\gamma \gt 0$
(
 $\gamma \lt 0$
), then the common trend component has a positive effect on both RPI and TFP (a positive effect on RPI and a negative effect on TFP), which would imply a positive (negative) covariation between the two series. This is essentially the argument in Benati (Reference Benati2013).
$\gamma \lt 0$
), then the common trend component has a positive effect on both RPI and TFP (a positive effect on RPI and a negative effect on TFP), which would imply a positive (negative) covariation between the two series. This is essentially the argument in Benati (Reference Benati2013). -
5. If
 $\varphi _{\mu } = 1$
and
$\varphi _{\mu } = 1$
and
 $\varphi _{\mu _{x}} = 1$
. This gives rise to the following smooth evolving processes for the trend:(8)
$\varphi _{\mu _{x}} = 1$
. This gives rise to the following smooth evolving processes for the trend:(8) \begin{equation} \Delta \tau _t = \zeta _1 1(t\lt T_{B}) + \zeta _2 1(t\geq T_{B}) + \Delta \tau _{t-1} + \eta _t, \end{equation}
(9)
\begin{equation} \Delta \tau _t = \zeta _1 1(t\lt T_{B}) + \zeta _2 1(t\geq T_{B}) + \Delta \tau _{t-1} + \eta _t, \end{equation}
(9) \begin{equation} \Delta \tau _{x,t} = \zeta _{x,1}1(t\lt T_{B}) + \zeta _{x,2}1(t\geq t_0) + \Delta \tau _{x,t-1} +\eta _{x,t}. \end{equation}
\begin{equation} \Delta \tau _{x,t} = \zeta _{x,1}1(t\lt T_{B}) + \zeta _{x,2}1(t\geq t_0) + \Delta \tau _{x,t-1} +\eta _{x,t}. \end{equation}
Through a model comparison exercise, we are able to properly assess the validity of each of these competing assumptions and their implications for estimation and inference in order to shed light on the appropriate representation between NT and IST.
3. Bayesian estimation
In this section, we provide the details of the priors and outline the Bayesian estimation of the unobserved components model in equations (1)–(6). In particular, we highlight how the model can be estimated efficiently using band matrix algorithms instead of conventional Kalman filter-based methods.
We assume proper but relatively noninformative priors for the model parameters
![]() $\gamma$
,
$\gamma$
,
![]() $\boldsymbol \phi =(\phi _{z,1},\phi _{z,2},\phi _{x,1},\phi _{x,2} )^{\prime }, \boldsymbol \varphi =(\varphi _{\mu },\varphi _{\mu _x})^{\prime }, \boldsymbol \zeta = (\zeta _1,\zeta _2,\zeta _{x,1},\zeta _{x,2})^{\prime }$
,
$\boldsymbol \phi =(\phi _{z,1},\phi _{z,2},\phi _{x,1},\phi _{x,2} )^{\prime }, \boldsymbol \varphi =(\varphi _{\mu },\varphi _{\mu _x})^{\prime }, \boldsymbol \zeta = (\zeta _1,\zeta _2,\zeta _{x,1},\zeta _{x,2})^{\prime }$
,
![]() $\boldsymbol \sigma ^2 = (\sigma _{\eta }^2, \sigma _{\eta _x}^2, \sigma _{z}^2, \sigma _{x}^2)^{\prime }$
, and
$\boldsymbol \sigma ^2 = (\sigma _{\eta }^2, \sigma _{\eta _x}^2, \sigma _{z}^2, \sigma _{x}^2)^{\prime }$
, and
![]() $\boldsymbol \tau _0$
. In particular, we adopt a normal prior for
$\boldsymbol \tau _0$
. In particular, we adopt a normal prior for
![]() $\gamma$
:
$\gamma$
:
![]() $\gamma \sim \mathcal{N}(\gamma _{0}, V_{\gamma })$
with
$\gamma \sim \mathcal{N}(\gamma _{0}, V_{\gamma })$
with
![]() $\gamma _{0} = 0$
and
$\gamma _{0} = 0$
and
![]() $V_{\gamma }=1$
. These values imply a weakly informative prior centered at 0. Moreover, we assume independent priors for
$V_{\gamma }=1$
. These values imply a weakly informative prior centered at 0. Moreover, we assume independent priors for
![]() $\boldsymbol \phi$
,
$\boldsymbol \phi$
,
![]() $\boldsymbol \varphi$
,
$\boldsymbol \varphi$
,
![]() $\boldsymbol \zeta$
and
$\boldsymbol \zeta$
and
![]() $\boldsymbol \tau _0$
:
$\boldsymbol \tau _0$
:
where
![]() $\textbf{R}$
denotes the stationarity region. The prior on the AR coefficients
$\textbf{R}$
denotes the stationarity region. The prior on the AR coefficients
![]() $\boldsymbol \phi$
affects how persistent the cyclical components are. We assume relatively large prior variances,
$\boldsymbol \phi$
affects how persistent the cyclical components are. We assume relatively large prior variances,
![]() $\textbf{V}_{\boldsymbol \phi } = \textbf{I}_4$
, so that a priori
$\textbf{V}_{\boldsymbol \phi } = \textbf{I}_4$
, so that a priori
![]() $\boldsymbol \phi$
can take on a wide range of values. The prior mean is assumed to be
$\boldsymbol \phi$
can take on a wide range of values. The prior mean is assumed to be
![]() $\boldsymbol \phi _0= (1.3, -0.7, 1.3, -0.7)^{\prime }$
, which implies that each of the two AR(2) processes has two complex roots, and they are relatively persistent. Similarly, for the prior on
$\boldsymbol \phi _0= (1.3, -0.7, 1.3, -0.7)^{\prime }$
, which implies that each of the two AR(2) processes has two complex roots, and they are relatively persistent. Similarly, for the prior on
![]() $\boldsymbol \varphi$
, we set
$\boldsymbol \varphi$
, we set
![]() $\textbf{V}_{\boldsymbol \varphi } = \textbf{I}_2$
with prior mean
$\textbf{V}_{\boldsymbol \varphi } = \textbf{I}_2$
with prior mean
![]() $\boldsymbol \varphi _0= (0.9, 0.9)^{\prime }$
, which implies that the two AR(1) processes are fairly persistent. Next, we assume that the priors on
$\boldsymbol \varphi _0= (0.9, 0.9)^{\prime }$
, which implies that the two AR(1) processes are fairly persistent. Next, we assume that the priors on
![]() $ \sigma _{z}^2$
and
$ \sigma _{z}^2$
and
![]() $\sigma _{x}^2$
are inverse-gamma:
$\sigma _{x}^2$
are inverse-gamma:
We set
![]() $\nu _{z} = \nu _{x} = 4$
,
$\nu _{z} = \nu _{x} = 4$
,
![]() $S_{z} = 6\times 10^{-5}$
, and
$S_{z} = 6\times 10^{-5}$
, and
![]() $S_{x} = 3\times 10^{-5}$
. These values imply prior means of
$S_{x} = 3\times 10^{-5}$
. These values imply prior means of
![]() $\sigma _{z}^2$
and
$\sigma _{z}^2$
and
![]() $\sigma _{x}^2$
to be, respectively,
$\sigma _{x}^2$
to be, respectively,
![]() $2\times 10^{-5}$
and
$2\times 10^{-5}$
and
![]() $S_{x} = 10^{-5}$
.
$S_{x} = 10^{-5}$
.
For
![]() $\sigma _{\eta }^2$
and
$\sigma _{\eta }^2$
and
![]() $\sigma _{\eta _x}^2$
, the error variances in the state equations (3) and (4), we follow the suggestion of Frühwirth-Schnatter and Wagner (Reference Frühwirth-Schnatter and Wagner2010) to use normal priors centered at 0 on the standard deviations
$\sigma _{\eta _x}^2$
, the error variances in the state equations (3) and (4), we follow the suggestion of Frühwirth-Schnatter and Wagner (Reference Frühwirth-Schnatter and Wagner2010) to use normal priors centered at 0 on the standard deviations
![]() $\sigma _{\eta }$
and
$\sigma _{\eta }$
and
![]() $\sigma _{\eta _x}$
. Compared to the conventional inverse-gamma prior, a normal prior centered at 0 has the advantage of not distorting the likelihood when the true value of the error variance is close to zero. In our implementation, we use the fact that a normal prior
$\sigma _{\eta _x}$
. Compared to the conventional inverse-gamma prior, a normal prior centered at 0 has the advantage of not distorting the likelihood when the true value of the error variance is close to zero. In our implementation, we use the fact that a normal prior
![]() $\sigma _{\eta }\sim \mathcal{N}(0,V_{\sigma _{\eta }})$
on the standard deviation implies gamma prior on the error variance
$\sigma _{\eta }\sim \mathcal{N}(0,V_{\sigma _{\eta }})$
on the standard deviation implies gamma prior on the error variance
![]() $\sigma _{\eta }^2$
:
$\sigma _{\eta }^2$
:
![]() $\sigma _{\eta }^2 \sim \mathcal{G}(1/2,1/(2V_{\sigma _{\eta }}))$
, where
$\sigma _{\eta }^2 \sim \mathcal{G}(1/2,1/(2V_{\sigma _{\eta }}))$
, where
![]() $\mathcal{G}(a, b)$
denotes the gamma distribution with mean
$\mathcal{G}(a, b)$
denotes the gamma distribution with mean
![]() $a/b$
. Similarly, we assume
$a/b$
. Similarly, we assume
![]() $\sigma _{\eta _x}^2 \sim \mathcal{G}(1/2,1/(2V_{\sigma _{\eta _x}}))$
. We set
$\sigma _{\eta _x}^2 \sim \mathcal{G}(1/2,1/(2V_{\sigma _{\eta _x}}))$
. We set
![]() $V_{\sigma _{\eta }} = 5\times 10^{-6}$
and
$V_{\sigma _{\eta }} = 5\times 10^{-6}$
and
![]() $V_{\sigma _{\eta _x}} = 5\times 10^{-5}.$
$V_{\sigma _{\eta _x}} = 5\times 10^{-5}.$
Next, we outline the posterior simulator to estimate the model in equations (1)–(6) with the priors described above. To that end, let
![]() $\boldsymbol \tau = (\tau _1,\tau _{x,1},\tau _2,\tau _{x,2},\ldots$
,
$\boldsymbol \tau = (\tau _1,\tau _{x,1},\tau _2,\tau _{x,2},\ldots$
,
![]() $\tau _T,\tau _{x,T})^{\prime }$
and
$\tau _T,\tau _{x,T})^{\prime }$
and
![]() $\textbf{y}=(z_1,x_1,\ldots, z_T,x_T)^{\prime }$
. Then, posterior draws can be obtained by sequentially sampling from the following conditional distributions:
$\textbf{y}=(z_1,x_1,\ldots, z_T,x_T)^{\prime }$
. Then, posterior draws can be obtained by sequentially sampling from the following conditional distributions:
-
1.
 $p(\boldsymbol \tau,\gamma \,|\, \textbf{y}, \boldsymbol \phi, \boldsymbol \varphi, \boldsymbol \zeta, \boldsymbol \sigma ^2,\boldsymbol \tau _0) = p(\gamma \,|\, \textbf{y}, \boldsymbol \phi, \boldsymbol \varphi, \boldsymbol \zeta, \boldsymbol \sigma ^2,\boldsymbol \tau _0) p(\boldsymbol \tau \,|\, \textbf{y}, \gamma, \boldsymbol \phi, \boldsymbol \varphi, \boldsymbol \zeta, \boldsymbol \sigma ^2,\boldsymbol \tau _0)$
;
$p(\boldsymbol \tau,\gamma \,|\, \textbf{y}, \boldsymbol \phi, \boldsymbol \varphi, \boldsymbol \zeta, \boldsymbol \sigma ^2,\boldsymbol \tau _0) = p(\gamma \,|\, \textbf{y}, \boldsymbol \phi, \boldsymbol \varphi, \boldsymbol \zeta, \boldsymbol \sigma ^2,\boldsymbol \tau _0) p(\boldsymbol \tau \,|\, \textbf{y}, \gamma, \boldsymbol \phi, \boldsymbol \varphi, \boldsymbol \zeta, \boldsymbol \sigma ^2,\boldsymbol \tau _0)$
; -
2.
 $p(\boldsymbol \phi \,|\, \textbf{y}, \boldsymbol \tau, \gamma, \boldsymbol \varphi, \boldsymbol \zeta, \boldsymbol \sigma ^2,\boldsymbol \tau _0)$
;
$p(\boldsymbol \phi \,|\, \textbf{y}, \boldsymbol \tau, \gamma, \boldsymbol \varphi, \boldsymbol \zeta, \boldsymbol \sigma ^2,\boldsymbol \tau _0)$
; -
3.
 $p(\boldsymbol \varphi \,|\, \textbf{y}, \boldsymbol \tau, \gamma, \boldsymbol \phi, \boldsymbol \zeta, \boldsymbol \sigma ^2,\boldsymbol \tau _0)$
;
$p(\boldsymbol \varphi \,|\, \textbf{y}, \boldsymbol \tau, \gamma, \boldsymbol \phi, \boldsymbol \zeta, \boldsymbol \sigma ^2,\boldsymbol \tau _0)$
; -
4.
 $p(\boldsymbol \sigma ^2 \,|\, \textbf{y}, \boldsymbol \tau, \gamma, \boldsymbol \phi, \boldsymbol \varphi, \boldsymbol \zeta,\boldsymbol \tau _0)$
;
$p(\boldsymbol \sigma ^2 \,|\, \textbf{y}, \boldsymbol \tau, \gamma, \boldsymbol \phi, \boldsymbol \varphi, \boldsymbol \zeta,\boldsymbol \tau _0)$
; -
5.
 $p(\boldsymbol \zeta,\boldsymbol \tau _0 \,|\, \textbf{y}, \boldsymbol \tau, \gamma, \boldsymbol \phi, \boldsymbol \varphi, \boldsymbol \sigma ^2)$
.
$p(\boldsymbol \zeta,\boldsymbol \tau _0 \,|\, \textbf{y}, \boldsymbol \tau, \gamma, \boldsymbol \phi, \boldsymbol \varphi, \boldsymbol \sigma ^2)$
.
We refer the readers to Appendix A.5 for implementation details of the posterior sampler.
4. Empirical results
In this section, we report parameter estimates of the bivariate unobserved components model defined in equations (1)–(6). The dataset consists of the time series of the logarithm of (the inverse of) RPI and TFP from
![]() $1959.II$
to
$1959.II$
to
![]() $2019.II$
. RPI is computed as the investment deflator divided by the consumption deflator, and it is easily accessible from the Federal Reserve Economic Database (FRED). While the complete description of the deflators along with the accompanying details of the computation of the series are found in DiCecio (Reference DiCecio2009), it is worth emphasizing that the investment deflator corresponds to the quality-adjusted investment deflator calculated following the approaches in Gordon (Reference Gordon1990), Cummins and Violante (Reference Cummins and Violante2002), and Fisher (Reference Fisher2006). On the other hand, we compute TFP based on the aggregate TFP growth, which is measured as the growth rate of the business sector TFP corrected for capital utilization. The capital utilization-adjusted aggregate TFP growth series is produced by Fernald (Reference Fernald2014) and is widely regarded as the best available measure of NT.Footnote
2
$2019.II$
. RPI is computed as the investment deflator divided by the consumption deflator, and it is easily accessible from the Federal Reserve Economic Database (FRED). While the complete description of the deflators along with the accompanying details of the computation of the series are found in DiCecio (Reference DiCecio2009), it is worth emphasizing that the investment deflator corresponds to the quality-adjusted investment deflator calculated following the approaches in Gordon (Reference Gordon1990), Cummins and Violante (Reference Cummins and Violante2002), and Fisher (Reference Fisher2006). On the other hand, we compute TFP based on the aggregate TFP growth, which is measured as the growth rate of the business sector TFP corrected for capital utilization. The capital utilization-adjusted aggregate TFP growth series is produced by Fernald (Reference Fernald2014) and is widely regarded as the best available measure of NT.Footnote
2
First, we perform statistical break tests to verify, as has been established in the empirical literature, that RPI experienced a break in its trend around early
![]() $1982$
. Following the recommendations in Bai and Perron (Reference Bai and Perron2003), we find a break date at
$1982$
. Following the recommendations in Bai and Perron (Reference Bai and Perron2003), we find a break date at
![]() $1982.I$
in the mean of the log difference of RPI as documented in Fisher (Reference Fisher2006), Justiniano et al. (Reference Justiniano, Primiceri and Tambalotti2011a, Reference Justiniano, Primiceri and Tambalotti2011b), and Benati (Reference Benati2013). In addition, a consequence of our specification is that RPI and TFP must share a common structural break. Consequently, we follow the methodology outlined in Qu and Perron (Reference Qu and Perron2007) to test whether or not the trends in the series are orthogonal.Footnote
3
The estimation results suggest that RPI and TFP might share a common structural break at
$1982.I$
in the mean of the log difference of RPI as documented in Fisher (Reference Fisher2006), Justiniano et al. (Reference Justiniano, Primiceri and Tambalotti2011a, Reference Justiniano, Primiceri and Tambalotti2011b), and Benati (Reference Benati2013). In addition, a consequence of our specification is that RPI and TFP must share a common structural break. Consequently, we follow the methodology outlined in Qu and Perron (Reference Qu and Perron2007) to test whether or not the trends in the series are orthogonal.Footnote
3
The estimation results suggest that RPI and TFP might share a common structural break at
![]() $1980.I$
. This break date falls within the confidence interval of the estimated break date between the same two time series,
$1980.I$
. This break date falls within the confidence interval of the estimated break date between the same two time series,
![]() $[1973.I,1982.III]$
, documented in Benati (Reference Benati2013). Therefore, the evidence from structural break tests does not rule out the presence of a single break at
$[1973.I,1982.III]$
, documented in Benati (Reference Benati2013). Therefore, the evidence from structural break tests does not rule out the presence of a single break at
![]() $1982.I$
in the common stochastic trend component of RPI and TFP.
$1982.I$
in the common stochastic trend component of RPI and TFP.
To jumpstart the discussion of the estimation results, we provide a graphical representation of the fit of our model as illustrated by the fitted values of the two series in Figure 1. It is clear from the graph that the bivariate unobserved components model is able to fit both series well with fairly narrow credible intervals.

Figure 1. Fitted values of
![]() $\widehat{z}_t = \tau _t$
and
$\widehat{z}_t = \tau _t$
and
![]() $\widehat{x}_t = \gamma \tau _t + \tau _{x,t}$
. The shaded region represents the 5-th and 95-th percentiles.
$\widehat{x}_t = \gamma \tau _t + \tau _{x,t}$
. The shaded region represents the 5-th and 95-th percentiles.
We report the estimates of model parameters in Table 1 and organize the discussion of our findings around the following two points: (1) the within-series relationship and (2) the cross-series relationship. At the same time, we elaborate on the econometric ramifications of these two points on the analysis of DSGE models.
Table 1. Posterior means, standard deviations, and 95% credible intervals of model parameters

4.1. The Within-Series Relationship in RPI and TFP
The within-series relationship is concerned with the relative importance of the permanent component and the transitory component in (the inverse of) RPI and TFP. This relationship is captured via the estimated values of (i) the drift parameters,
![]() $\zeta$
and
$\zeta$
and
![]() $\zeta _{x}$
, (ii) the autoregressive parameters of the permanent components in RPI and TFP,
$\zeta _{x}$
, (ii) the autoregressive parameters of the permanent components in RPI and TFP,
![]() $\varphi _{\mu }$
and
$\varphi _{\mu }$
and
![]() $\varphi _{\mu _x}$
, (iii) the autoregressive parameters of the transitory components in RPI and TFP,
$\varphi _{\mu _x}$
, (iii) the autoregressive parameters of the transitory components in RPI and TFP,
![]() $\phi _{z,1}$
,
$\phi _{z,1}$
,
![]() $\phi _{z,2}$
,
$\phi _{z,2}$
,
![]() $\phi _{x,1}$
, and
$\phi _{x,1}$
, and
![]() $\phi _{x,2}$
, (iv) and the standard deviations of the permanent and transitory components,
$\phi _{x,2}$
, (iv) and the standard deviations of the permanent and transitory components,
![]() $\sigma _{\eta }$
,
$\sigma _{\eta }$
,
![]() $\sigma _{\eta _{x}}$
,
$\sigma _{\eta _{x}}$
,
![]() $\sigma _{z}$
, and
$\sigma _{z}$
, and
![]() $\sigma _{x}$
.
$\sigma _{x}$
.
First, it is evident from Figure 2 that the estimated trend in RPI,
![]() $\tau _t$
, is strongly trending upward, especially after the break at
$\tau _t$
, is strongly trending upward, especially after the break at
![]() $1982.I$
. In fact, the growth rate of
$1982.I$
. In fact, the growth rate of
![]() $\tau _t$
has more than doubled after
$\tau _t$
has more than doubled after
![]() $1982.I$
: as reported in Table 1, the posterior means of
$1982.I$
: as reported in Table 1, the posterior means of
![]() $\zeta _{1}$
and
$\zeta _{1}$
and
![]() $\zeta _{2}$
are 0.004 and 0.009, respectively. This is consistent with the narrative that the decline in the mean growth of RPI has accelerated in the period after
$\zeta _{2}$
are 0.004 and 0.009, respectively. This is consistent with the narrative that the decline in the mean growth of RPI has accelerated in the period after
![]() $1982.I$
, and this acceleration has been facilitated by the rapid price decline in information processing equipment and software. In contrast, the estimated trend
$1982.I$
, and this acceleration has been facilitated by the rapid price decline in information processing equipment and software. In contrast, the estimated trend
![]() $\tau _{x,t}$
shows gradual decline after
$\tau _{x,t}$
shows gradual decline after
![]() $1982.I$
—its growth rate decreases from 0.001 before the break to
$1982.I$
—its growth rate decreases from 0.001 before the break to
![]() $- 0.003$
after the break, although both figures are not statistically different from zero. Overall, it appears that trends in both series are captured completely by the stochastic trend component in RPI, and this piece of evidence provides additional support that GPT might be an important driver of the growth in TFP in the USA.
$- 0.003$
after the break, although both figures are not statistically different from zero. Overall, it appears that trends in both series are captured completely by the stochastic trend component in RPI, and this piece of evidence provides additional support that GPT might be an important driver of the growth in TFP in the USA.
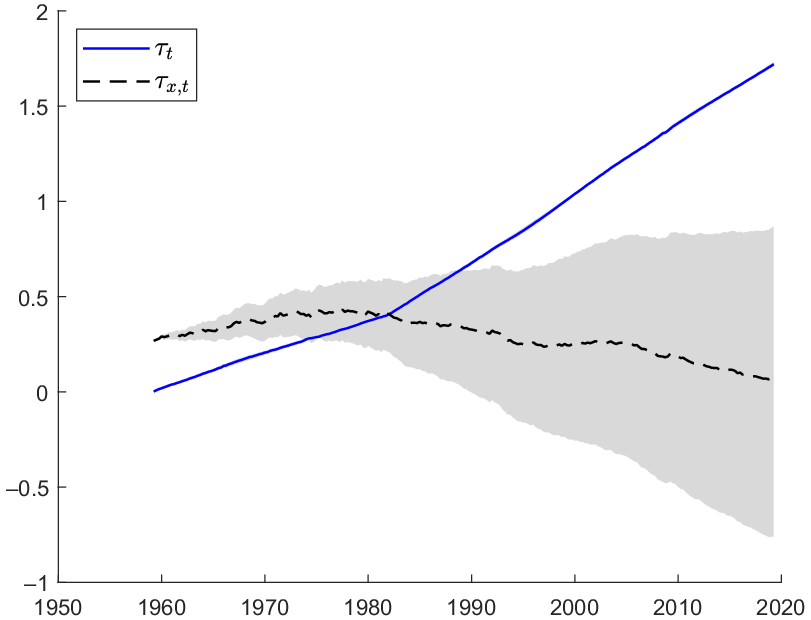
Figure 2. Posterior means of
![]() $\tau _t$
and
$\tau _t$
and
![]() $\tau _{x,t}$
. The shaded region represents the 16-th and 84-th percentiles.
$\tau _{x,t}$
. The shaded region represents the 16-th and 84-th percentiles.
Moving on to the estimated autoregressive parameters of the permanent component,
![]() $\widehat{\varphi }_{\mu } = 0.101$
and
$\widehat{\varphi }_{\mu } = 0.101$
and
![]() $\widehat{\varphi }_{\mu _x} = -0.051$
, we note that growths in RPI and TFP do not appear to be as serially correlated as reported in the empirical literature. For instance, Justiniano et al. (Reference Justiniano, Primiceri and Tambalotti2011a, Reference Justiniano, Primiceri and Tambalotti2011b) report a posterior median value of 0.287 for the investment-specific technological process and 0.163 for NT. With regard to the AR(2) processes that describe the transitory components in RPI and TFP, the estimated autoregressive parameters indicate that these components are relatively more persistent than the growth components of the series.
$\widehat{\varphi }_{\mu _x} = -0.051$
, we note that growths in RPI and TFP do not appear to be as serially correlated as reported in the empirical literature. For instance, Justiniano et al. (Reference Justiniano, Primiceri and Tambalotti2011a, Reference Justiniano, Primiceri and Tambalotti2011b) report a posterior median value of 0.287 for the investment-specific technological process and 0.163 for NT. With regard to the AR(2) processes that describe the transitory components in RPI and TFP, the estimated autoregressive parameters indicate that these components are relatively more persistent than the growth components of the series.
Furthermore, the estimated values of the variance of the innovations lead to some interesting observations. The variance of the idiosyncratic growth rate in TFP,
![]() $\sigma _{\eta _x}^2 = 5.17\times 10^{-5}$
, is larger than its counterpart for the transitory component,
$\sigma _{\eta _x}^2 = 5.17\times 10^{-5}$
, is larger than its counterpart for the transitory component,
![]() $\sigma _{x}^2 = 7.76\times 10^{-6}$
. On the other hand, the variance of the growth rate in RPI,
$\sigma _{x}^2 = 7.76\times 10^{-6}$
. On the other hand, the variance of the growth rate in RPI,
![]() $\sigma _{\eta }^2 = 5.51\times 10^{-6}$
, is smaller than the variance of its transitory component,
$\sigma _{\eta }^2 = 5.51\times 10^{-6}$
, is smaller than the variance of its transitory component,
![]() $\sigma _{z}^2 = 1.79\times 10^{-5}$
.
$\sigma _{z}^2 = 1.79\times 10^{-5}$
.
Overall, these results seem to indicate that (i) RPI and TFP appear to follow an ARIMA(1,1,0) process, (ii) RPI and TFP growths are only weakly serially correlated, (iii) transitory components in RPI and TFP are relatively more persistent than the growth components on these series, (iv) TFP growth shocks generate more variability than shocks to the growth rate of RPI, and (v) shocks to the transitory component of RPI are more volatile than shocks to the growth rate of RPI.
Now, we discuss the implications of these findings on the analysis of business cycle models. First, information about the process underlying RPI and TFP helps to reduce errors associated with the specification of idiosyncratic trends in DSGE models. Macro variables such as output are highly persistent. To capture this feature, researchers must typically take a stand on the specification of the trend in DSGE models. Since output typically inherits the trend properties of TFP and/or RPI, having accurate information about the trend properties of TFP and/or RPI should allow the researcher to minimize the possibility of trend misspecification which in turn has significant consequences on estimation and inference. Specifically, DSGE models are typically built to explain the cyclical movements in the data. Therefore, preliminary data transformation, in the form of removing secular trend variations, are oftentimes required before the estimation of the structural parameters. One alternative entails arbitrarily building into the model a noncyclical component of NT and/or IST and filtering the raw data using the model-based specification. Therefore, trend misspecifications may lead to inappropriate filtering approaches and erroneous conclusions. In fact, Singleton (Reference Singleton1988) documents that inadequate filtering generally leads to inconsistent estimates of the parameters. Similarly, Canova (Reference Canova2014) recently demonstrates that the posterior distribution of the structural parameters vary greatly with the preliminary transformations (linear detrending, Hodrick and Prescott filtering, growth rate filtering, and band-pass filtering) used to remove secular trends. Consequently, this translates into significant differences in the impulse and propagation of shocks. Furthermore, Cogley and Nason (Reference Cogley and Nason1995b) show that it is hard to interpret results from filtered data as facts or artifacts about business cycles as filtering may generate spurious cycles in difference stationary and trend stationary processes. For example, the authors find that a model may exhibit business cycle periodicity and comovement in filtered data even when such phenomena are not present in the data.
Second, information about the process underlying RPI and TFP improves our understanding of the analysis of macro dynamics. Researchers typically analyze the dynamics of output and other macro variables along three dimensions over short horizons: the periodicity of output, comovement of macro variables with respect to output, and the relative volatility of macro variables. Specifically, in macro models, periodicity is usually measured by the autocorrelation function of output, and Cogley and Nason (Reference Cogley and Nason1993) and Cogley and Nason (Reference Cogley and Nason1995a) show that the periodicity of output is essentially determined by impulse dynamics. Several studies document that output growth is positively correlated over short horizons, and standard macro models struggle to generate this pattern. Consequently, in models where technology followed an ARIMA (1,1,0) process, output growth would inherit the AR(1) structure of TFP growth, and the model would be able to match the periodicity of output in the data. This point is particularly important as it relates to the responses of macro variables to exogenous shocks. Cogley and Nason (Reference Cogley and Nason1995a) highlight that macro variables, and output especially, contain a trend-reverting component that has a hump-shaped impulse response function. Since the response of output to technology shock, for instance, pretty much matches the response of technology itself, Cogley and Nason (Reference Cogley and Nason1995a) argue that exogenous shocks must produce this hump-shaped pattern for the model to match the facts about autocorrelated output growth. Ultimately, if the goal of the researcher is to match the periodicity of output in a way that the model also matches the time series characteristics of the impulse dynamics, then the choice of the trend is paramount in the specification of the model.
In addition, information about the volatilities and persistence of the processes underlying technology shocks may strengthen our inference on the relative importance of these shocks on fluctuations. As demonstrated in Canova (Reference Canova2014), the estimates of structural parameters depend on nuisance features such as the persistence and the volatility of the shocks, and misspecification of these nuisance features generates biased estimates of impact and persistence coefficients and leads to incorrect conclusions about the relative importance of the shocks.
4.2 The Cross-Series Relationship between (the Inverse of) RPI and TFP
We can evaluate the cross-series relationship through the estimated value of the parameter that captures the extent of the relationship between the trends in RPI and TFP, namely,
![]() $\gamma$
.
$\gamma$
.
First, the positive value of
![]() $\widehat{\gamma }$
implies a positive long-run co-variation between (the inverse of) RPI and TFP as established in Benati (Reference Benati2013). In addition, the estimated value of the parameter
$\widehat{\gamma }$
implies a positive long-run co-variation between (the inverse of) RPI and TFP as established in Benati (Reference Benati2013). In addition, the estimated value of the parameter
![]() $\gamma$
, (
$\gamma$
, (
![]() $\widehat{\gamma } = 0.478$
), is significantly different from zero and quite large. This result supplements the qualitative findings by providing a quantitative measure of scale differences in the trends of RPI and TFP. From a econometric point of view, we may interpret
$\widehat{\gamma } = 0.478$
), is significantly different from zero and quite large. This result supplements the qualitative findings by providing a quantitative measure of scale differences in the trends of RPI and TFP. From a econometric point of view, we may interpret
![]() $\widehat{\gamma }$
as the elasticity of TFP to IST changes. In that case, we may assert that, for the time period
$\widehat{\gamma }$
as the elasticity of TFP to IST changes. In that case, we may assert that, for the time period
![]() $1959.II$
to
$1959.II$
to
![]() $2019.II$
considered in this study, a 1% change in IST progress leads to a 0.478% increase in aggregate TFP. These observations are consistent with the view that permanent changes in RPI, which may reflect improvements in information communication technologies, might be representation of innovations in GPT. In fact, using industry-level data, Cummins and Violante (Reference Cummins and Violante2002) and Basu et al. (Reference Basu, Fernald and Oulton2003) find that improvements in information communication technologies contributed to productivity growth in the 1990s in essentially every industry in the USA. Moreover, Jorgenson et al. (Reference Jorgenson, Ho, Samuels and Stiroh2007) show that much of the TFP gain in the USA in the 2000s originated in industries that are the most intensive users of IT.
$2019.II$
considered in this study, a 1% change in IST progress leads to a 0.478% increase in aggregate TFP. These observations are consistent with the view that permanent changes in RPI, which may reflect improvements in information communication technologies, might be representation of innovations in GPT. In fact, using industry-level data, Cummins and Violante (Reference Cummins and Violante2002) and Basu et al. (Reference Basu, Fernald and Oulton2003) find that improvements in information communication technologies contributed to productivity growth in the 1990s in essentially every industry in the USA. Moreover, Jorgenson et al. (Reference Jorgenson, Ho, Samuels and Stiroh2007) show that much of the TFP gain in the USA in the 2000s originated in industries that are the most intensive users of IT.
In addition, this finding contributes to the debate about the specification of common trends and the source of business cycle fluctuations in DSGE models. In particular, Schmitt-Grohé and Uribè (Reference Schmitt-Grohé and Uribè2011) and Benati (Reference Benati2013) explore the relationship between RPI and TFP through the lenses of statistical tests of units root and co-integration, and the potential implications of such relationship on the role of technology shocks in economic fluctuations. Using quarterly US data over the period from
![]() $1948.I$
to
$1948.I$
to
![]() $2006.IV$
, Schmitt-Grohé and Uribè (Reference Schmitt-Grohé and Uribè2011) find that RPI and TFP contain a nonstationary stochastic component which is common to both series. In other words, TFP and RPI are co-integrated, which implies that NT and IST should be modeled as containing a common stochastic trend. Therefore, Schmitt-Grohé and Uribè (Reference Schmitt-Grohé and Uribè2011) estimate a DSGE model that imposes this result and identify a new source of business cycle fluctuations: shocks to the common stochastic trend in neutral and investment-specific productivity. They find that the shocks play a sizable role in driving business cycle fluctuations as they explain three-fourth of the variances of output and investment growth and about one-third of the predicted variances of consumption growth and hours worked. If such results were validated, they would reshape the common approach of focusing on the importance of either NT or IST distinctively.
$2006.IV$
, Schmitt-Grohé and Uribè (Reference Schmitt-Grohé and Uribè2011) find that RPI and TFP contain a nonstationary stochastic component which is common to both series. In other words, TFP and RPI are co-integrated, which implies that NT and IST should be modeled as containing a common stochastic trend. Therefore, Schmitt-Grohé and Uribè (Reference Schmitt-Grohé and Uribè2011) estimate a DSGE model that imposes this result and identify a new source of business cycle fluctuations: shocks to the common stochastic trend in neutral and investment-specific productivity. They find that the shocks play a sizable role in driving business cycle fluctuations as they explain three-fourth of the variances of output and investment growth and about one-third of the predicted variances of consumption growth and hours worked. If such results were validated, they would reshape the common approach of focusing on the importance of either NT or IST distinctively.
However, Benati (Reference Benati2013) expresses some doubt about the co-integration results in Schmitt-Grohé and Uribè (Reference Schmitt-Grohé and Uribè2011). He claims that TFP and RPI are most likely not co-integrated, and he traces the origin of this finding of co-integration to the use of an inconsistent criteria for lag order selection in the Johansen procedure. When he uses the Schwartz information criterion (SIC) and Hannah–Quinn (HQ) criterion, the Johansen test points to no co-integration. Yet, he establishes that although the two series may not be co-integrated, they may still share a common stochastic nonstationary component. Using an approach proposed by Cochrane and Sbordone (Reference Cochrane and Sbordone1988) that searches for a statistically significant extent of co-variation between the two series’ long-horizon differences, Benati (Reference Benati2013) suggests that the evidence from his analysis points toward a common
![]() $I(1)$
component that induces a positive co-variation between TFP and RPI at long horizons. Then, he uses such restrictions in a vector autoregression (VAR) to identify common RPI and TFP component shocks and finds that the shocks play a sizable role in the fluctuations of TFP, RPI, and output: about 30% of the variability of RPI and TFP and 28% of the variability in output.
$I(1)$
component that induces a positive co-variation between TFP and RPI at long horizons. Then, he uses such restrictions in a vector autoregression (VAR) to identify common RPI and TFP component shocks and finds that the shocks play a sizable role in the fluctuations of TFP, RPI, and output: about 30% of the variability of RPI and TFP and 28% of the variability in output.
First, the results from our analysis complements the investigation in Schmitt-Grohé and Uribè (Reference Schmitt-Grohé and Uribè2011) and Benati (Reference Benati2013). The relatively large estimate of
![]() $\gamma$
validates the notion that NT and IST should not be modeled in DSGE models as emanating from orthogonal processes. While the two studies may disagree about the exact nature of the relationship between NT and IST, both share the common view that their underlying processes are not independent of each other as shown by the results herein, and disturbances to the process that joins them play a significant role in fluctuations of economic activity. This indicates, obviously, that a proper accounting, based on the time series properties of RPI and TFP, of the joint specification of NT and IST is necessary to address succinctly questions of economic fluctuations as common trend misspecification provide inexact conclusions about the role of shocks in economic fluctuations. For instance, papers that have approached the question about the source of fluctuations from the perspective of general equilibrium models have generated diverging results, partly because of the specification of NT and IST. In Justiniano et al. (Reference Justiniano, Primiceri and Tambalotti2011a), investment(-specific) shocks account for most of the business cycle variations in output, hours, and investment (at least 50%), while NT shocks play a minimal role. On the hand, the findings in Smets and Wouters (Reference Smets and Wouters2007) flip the script: the authors find that NT (and wage mark up) shocks account for most of the output variations, while investment(-specific) shocks play no role. Nonetheless, these two studies share the common feature that the processes underlying NT and IST are orthogonal to each other. As we discussed above, when Schmitt-Grohé and Uribè (Reference Schmitt-Grohé and Uribè2011) impose a common trend specification between the two types of technology, neither shocks matter for fluctuations: a new shock, the common stochastic trend shocks, emerges as the main source of business cycle fluctuations. Our framework offers a structural way to assimilate the common trend specification in DSGE models and evaluate the effects of such specifications in fluctuations. The typical approach to trend specification in DSGE models is to build a noncyclical component into the model via unit roots in NT and/or IST and filtering the raw data using the model-based transformation. However, this practice produces, in addition to inexact results about sources of fluctuations, counterfactual trend implications because they incorporate balanced growth path restrictions that are to some extent violated in the data. Therefore, Ferroni (Reference Ferroni2011) and Canova (Reference Canova2014) recommend an alternative one-step estimation approach that allows to specify a reduced-form representation of the trend component, which is ultimately combined to the DSGE model for estimation. Our results about the time series characteristics of RPI and TFP provide some guidance on the specification of such reduced-form models. Fernández-Villaverde et al. (Reference Fernández-Villaverde, Rubio-Ramirez and Schorfheide2016) recommend this alternative approach as one of the most desirable and promising approach to modeling trends in DSDE models. Furthermore, our framework distances itself from statistical tests and their associated issues of lag order and low power as the debate about the long-run relationship between RPI and TFP has thus far depended on the selection of lag order in the Johansen’s test. Also, our framework incorporates Schmitt-Grohé and Uribè (Reference Schmitt-Grohé and Uribè2011)’s result of co-integration and Benati (Reference Benati2013)’s finding of co-variation as special cases.
$\gamma$
validates the notion that NT and IST should not be modeled in DSGE models as emanating from orthogonal processes. While the two studies may disagree about the exact nature of the relationship between NT and IST, both share the common view that their underlying processes are not independent of each other as shown by the results herein, and disturbances to the process that joins them play a significant role in fluctuations of economic activity. This indicates, obviously, that a proper accounting, based on the time series properties of RPI and TFP, of the joint specification of NT and IST is necessary to address succinctly questions of economic fluctuations as common trend misspecification provide inexact conclusions about the role of shocks in economic fluctuations. For instance, papers that have approached the question about the source of fluctuations from the perspective of general equilibrium models have generated diverging results, partly because of the specification of NT and IST. In Justiniano et al. (Reference Justiniano, Primiceri and Tambalotti2011a), investment(-specific) shocks account for most of the business cycle variations in output, hours, and investment (at least 50%), while NT shocks play a minimal role. On the hand, the findings in Smets and Wouters (Reference Smets and Wouters2007) flip the script: the authors find that NT (and wage mark up) shocks account for most of the output variations, while investment(-specific) shocks play no role. Nonetheless, these two studies share the common feature that the processes underlying NT and IST are orthogonal to each other. As we discussed above, when Schmitt-Grohé and Uribè (Reference Schmitt-Grohé and Uribè2011) impose a common trend specification between the two types of technology, neither shocks matter for fluctuations: a new shock, the common stochastic trend shocks, emerges as the main source of business cycle fluctuations. Our framework offers a structural way to assimilate the common trend specification in DSGE models and evaluate the effects of such specifications in fluctuations. The typical approach to trend specification in DSGE models is to build a noncyclical component into the model via unit roots in NT and/or IST and filtering the raw data using the model-based transformation. However, this practice produces, in addition to inexact results about sources of fluctuations, counterfactual trend implications because they incorporate balanced growth path restrictions that are to some extent violated in the data. Therefore, Ferroni (Reference Ferroni2011) and Canova (Reference Canova2014) recommend an alternative one-step estimation approach that allows to specify a reduced-form representation of the trend component, which is ultimately combined to the DSGE model for estimation. Our results about the time series characteristics of RPI and TFP provide some guidance on the specification of such reduced-form models. Fernández-Villaverde et al. (Reference Fernández-Villaverde, Rubio-Ramirez and Schorfheide2016) recommend this alternative approach as one of the most desirable and promising approach to modeling trends in DSDE models. Furthermore, our framework distances itself from statistical tests and their associated issues of lag order and low power as the debate about the long-run relationship between RPI and TFP has thus far depended on the selection of lag order in the Johansen’s test. Also, our framework incorporates Schmitt-Grohé and Uribè (Reference Schmitt-Grohé and Uribè2011)’s result of co-integration and Benati (Reference Benati2013)’s finding of co-variation as special cases.
Finally, our findings about the fact that TFP may contain two nonstationary components contributes to the VAR literature about the identification of technology shocks and their role in business cycle fluctuations. Specifically, using a bivariate system consisting of the log difference of labor productivity and hours worked, Gali (Reference Gali1999) assesses the role of technology in generating fluctuations by identifying a (neutral) technology shock under the restriction (which could be derived from most standard RBC models) that only such shocks may have a permanent effect on the log level of labor productivity. An (implicit) underlying assumption of this long-run restriction is that the unit root in labor productivity is driven exclusively by (neutral) technology. Fisher (Reference Fisher2006) extended Gali (Reference Gali1999)’s framework to show that IST shocks may also have a permanent effect on the log level of labor productivity, and they play an significant role in generating fluctuations in economic variables. While both authors consider labor productivity as the key variable to their identification process, their argument may easily be applied to the case when we consider TFP instead. In Appendix A.1, we demonstrate that if output is measured in consumption units, only NT affects TFP permanently. However, when output is tabulated according to the Divisia index, both NT and IST permanently affect TFP. Therefore, our UC framework provides a theoretical structure to derive sensible and equally valid long-run restrictions about RPI and TFP, in the spirit of Gali (Reference Gali1999) and Fisher (Reference Fisher2006), to identify NT and IST shocks in a VAR framework.
5. Model comparison
In this section, we explore the fit of our bivariate unobserved components model defined in equations (1)–(6) to alternative restricted specifications that encompass the various assumptions in the theoretical and empirical literature. Therefore, our model constitutes a complete laboratory that may be used to evaluate the plausibility of competing specifications and their probable ramifications for business cycle analysis.
We adopt the Bayesian model comparison framework to compare various specifications via the Bayes factor. More specifically, suppose we wish to compare model
![]() $M_0$
against model
$M_0$
against model
![]() $M_1$
. Each model
$M_1$
. Each model
![]() $M_i, i=0,1,$
is formally defined by a likelihood function
$M_i, i=0,1,$
is formally defined by a likelihood function
![]() $p(\textbf{y}\,|\, \boldsymbol \theta _{i}, M_{i})$
and a prior distribution on the model-specific parameter vector
$p(\textbf{y}\,|\, \boldsymbol \theta _{i}, M_{i})$
and a prior distribution on the model-specific parameter vector
![]() $\boldsymbol \theta _{i}$
denoted by
$\boldsymbol \theta _{i}$
denoted by
![]() $p(\boldsymbol \theta _i \,|\, M_i)$
. Then, the Bayes factor in favor of
$p(\boldsymbol \theta _i \,|\, M_i)$
. Then, the Bayes factor in favor of
![]() $M_0$
against
$M_0$
against
![]() $M_1$
is defined as:
$M_1$
is defined as:
where
![]() $ p(\textbf{y}\,|\, M_{i}) = \int p(\textbf{y}\,|\, \boldsymbol \theta _{i}, M_{i}) p(\boldsymbol \theta _{i}\,|\, M_{i})\mathrm{d}\boldsymbol \theta _{i}$
is the marginal likelihood under model
$ p(\textbf{y}\,|\, M_{i}) = \int p(\textbf{y}\,|\, \boldsymbol \theta _{i}, M_{i}) p(\boldsymbol \theta _{i}\,|\, M_{i})\mathrm{d}\boldsymbol \theta _{i}$
is the marginal likelihood under model
![]() $M_i$
,
$M_i$
,
![]() $i=0,1$
. Note that the marginal likelihood is the marginal data density (unconditional on the prior distribution) implied by model
$i=0,1$
. Note that the marginal likelihood is the marginal data density (unconditional on the prior distribution) implied by model
![]() $M_i$
evaluated at the observed data
$M_i$
evaluated at the observed data
![]() $\textbf{y}$
. Since the marginal likelihood can be interpreted as a joint density forecast evaluated at the observed data, it has a built-in penalty for model complexity. If the observed data are likely under the model, the associated marginal likelihood would be “large” and vice versa. It follows that
$\textbf{y}$
. Since the marginal likelihood can be interpreted as a joint density forecast evaluated at the observed data, it has a built-in penalty for model complexity. If the observed data are likely under the model, the associated marginal likelihood would be “large” and vice versa. It follows that
![]() $\mathrm{BF}_{01}\gt 1$
indicates evidence in favor of model
$\mathrm{BF}_{01}\gt 1$
indicates evidence in favor of model
![]() $M_0$
against
$M_0$
against
![]() $M_1$
, and the weight of evidence is proportional to the value of the Bayes factor. For a textbook treatment of the Bayes factor and the computation of the marginal likelihood, see Chan et al. (Reference Chan, Koop, Poirier and Tobias2019).
$M_1$
, and the weight of evidence is proportional to the value of the Bayes factor. For a textbook treatment of the Bayes factor and the computation of the marginal likelihood, see Chan et al. (Reference Chan, Koop, Poirier and Tobias2019).
5.1. Testing
 $\gamma = 0$
$\gamma = 0$
In the first modified model, we impose the restriction that
![]() $\gamma = 0$
, which essentially amounts to testing the GPT theory. If the restricted model were preferred over the unrestricted model, then the trends in RPI and TFP would be orthogonal, and the traditional approach of specifying NT and IST would be well founded.
$\gamma = 0$
, which essentially amounts to testing the GPT theory. If the restricted model were preferred over the unrestricted model, then the trends in RPI and TFP would be orthogonal, and the traditional approach of specifying NT and IST would be well founded.
The posterior mean of
![]() $\gamma$
is estimated to be about
$\gamma$
is estimated to be about
![]() $0.48$
, and the posterior standard deviation is 0.55. Most of the mass of the posterior distribution is on positive values—the posterior probability that
$0.48$
, and the posterior standard deviation is 0.55. Most of the mass of the posterior distribution is on positive values—the posterior probability that
![]() $\gamma \gt 0$
is 0.88. To formally test if
$\gamma \gt 0$
is 0.88. To formally test if
![]() $\gamma =0$
, we compute the Bayes factor in favor of the baseline model in equations (1)–(6) against the unrestricted version with
$\gamma =0$
, we compute the Bayes factor in favor of the baseline model in equations (1)–(6) against the unrestricted version with
![]() $\gamma =0$
imposed. In this case, the Bayes factor can be obtained by using the Savage–Dickey density ratio
$\gamma =0$
imposed. In this case, the Bayes factor can be obtained by using the Savage–Dickey density ratio
![]() $p(\gamma =0)/p(\gamma =0\,|\, \textbf{y})$
.Footnote
4
$p(\gamma =0)/p(\gamma =0\,|\, \textbf{y})$
.Footnote
4
The Bayes factor in favor of the baseline model is about 1.1, suggesting that even though there is some evidence against the hypothesis
![]() $\gamma =0$
, the evidence is not strong. To better understand this result, we plot the prior and posterior distributions of
$\gamma =0$
, the evidence is not strong. To better understand this result, we plot the prior and posterior distributions of
![]() $\gamma$
in Figure 3. As is clear from the figure, the prior and posterior densities at
$\gamma$
in Figure 3. As is clear from the figure, the prior and posterior densities at
![]() $\gamma =0$
have similar values. However, it is also apparent that the data move the prior distribution to the right, making larger values of
$\gamma =0$
have similar values. However, it is also apparent that the data move the prior distribution to the right, making larger values of
![]() $\gamma$
more likely under the posterior distribution. Hence, there seems to be some support for the hypothesis that
$\gamma$
more likely under the posterior distribution. Hence, there seems to be some support for the hypothesis that
![]() $\gamma \gt 0$
. More importantly, this result confirms the fact that
$\gamma \gt 0$
. More importantly, this result confirms the fact that
![]() $\gamma \neq 0$
, and the approach of modeling NT and IST as following independent processes is clearly not supported by the data. As we amply discussed in Section 4.2, such common trend misspecification yields incorrect restrictions about balanced growth restrictions and invalid conclusions about the main sources of business cycle fluctuations. Therefore, this suggest that business cycle researchers need to modify the specification of DSGE models to consider the possibility of the existence of this long-run joint relationship observed in the data and its potential effect on fluctuations.
$\gamma \neq 0$
, and the approach of modeling NT and IST as following independent processes is clearly not supported by the data. As we amply discussed in Section 4.2, such common trend misspecification yields incorrect restrictions about balanced growth restrictions and invalid conclusions about the main sources of business cycle fluctuations. Therefore, this suggest that business cycle researchers need to modify the specification of DSGE models to consider the possibility of the existence of this long-run joint relationship observed in the data and its potential effect on fluctuations.

Figure 3. Prior and posterior distributions of
![]() $\gamma$
.
$\gamma$
.
5.2. Testing
 $\varphi _\mu = \varphi _{\mu _x} =0$
$\varphi _\mu = \varphi _{\mu _x} =0$
Next, we test the joint hypothesis that
![]() $\varphi _\mu = \varphi _{\mu _x} =0$
. In this case, the restricted model would allow the trend component to follow a random walk plus drift process such that the growths in RPI and TFP are constant. This would capture the assumptions in Fisher (Reference Fisher2006).
$\varphi _\mu = \varphi _{\mu _x} =0$
. In this case, the restricted model would allow the trend component to follow a random walk plus drift process such that the growths in RPI and TFP are constant. This would capture the assumptions in Fisher (Reference Fisher2006).
Again the Bayes factor in favor of the baseline model against the restricted model with
![]() $\varphi _\mu = \varphi _{\mu _x} =0$
imposed can be obtained by computing the Savage–Dickey density ratio
$\varphi _\mu = \varphi _{\mu _x} =0$
imposed can be obtained by computing the Savage–Dickey density ratio
![]() $p(\varphi _\mu = 0, \varphi _{\mu _x} =0)/ p(\varphi _\mu = 0, \varphi _{\mu _x} = 0\,|\, \textbf{y})$
. The Bayes factor in favor of the restricted model with
$p(\varphi _\mu = 0, \varphi _{\mu _x} =0)/ p(\varphi _\mu = 0, \varphi _{\mu _x} = 0\,|\, \textbf{y})$
. The Bayes factor in favor of the restricted model with
![]() $\varphi _\mu = \varphi _{\mu _x} =0$
is about 14. This indicates that there is strong evidence in favor of the hypothesis
$\varphi _\mu = \varphi _{\mu _x} =0$
is about 14. This indicates that there is strong evidence in favor of the hypothesis
![]() $\varphi _\mu = \varphi _{\mu _x} =0$
. This is consistent with the estimation results reported in Table 1—the estimates of
$\varphi _\mu = \varphi _{\mu _x} =0$
. This is consistent with the estimation results reported in Table 1—the estimates of
![]() $\varphi _\mu$
and
$\varphi _\mu$
and
![]() $ \varphi _{\mu _x}$
are both small in magnitude with relatively large posterior standard deviations. This is an example where the Bayes factor favors a simpler, more restrictive model.
$ \varphi _{\mu _x}$
are both small in magnitude with relatively large posterior standard deviations. This is an example where the Bayes factor favors a simpler, more restrictive model.
Despite restricting
![]() $\varphi _\mu = \varphi _{\mu _x} =0$
, this restricted model is able to fit the RPI and TFP series very well, as shown in Figure 4. This suggests that an ARIMA(0,1,0) specification for NT and IST would also be a viable alternative in DSGE models. Nonetheless, an ARIMA(0,1,0) specification, which implies a constant growth rate, would be incapable of generating the positive autocorrelated AR(1) observed in output growth. As we mentioned in Section 4.1, Cogley and Nason (Reference Cogley and Nason1995a) show that output dynamics are essentially determined by impulse dynamics. Therefore, DSGE models would be able to match the periodicity of output if the process of technology is simulated to have a positively autocorrelated growth rate. In addition, Cogley and Nason (Reference Cogley and Nason1995a) demonstrate that an ARIMA(1,1,0) only would be needed to produce a hump-shaped response of output in order for models to match these facts about autocorrelated output growth.
$\varphi _\mu = \varphi _{\mu _x} =0$
, this restricted model is able to fit the RPI and TFP series very well, as shown in Figure 4. This suggests that an ARIMA(0,1,0) specification for NT and IST would also be a viable alternative in DSGE models. Nonetheless, an ARIMA(0,1,0) specification, which implies a constant growth rate, would be incapable of generating the positive autocorrelated AR(1) observed in output growth. As we mentioned in Section 4.1, Cogley and Nason (Reference Cogley and Nason1995a) show that output dynamics are essentially determined by impulse dynamics. Therefore, DSGE models would be able to match the periodicity of output if the process of technology is simulated to have a positively autocorrelated growth rate. In addition, Cogley and Nason (Reference Cogley and Nason1995a) demonstrate that an ARIMA(1,1,0) only would be needed to produce a hump-shaped response of output in order for models to match these facts about autocorrelated output growth.

Figure 4. Fitted values of
![]() $\widehat{z}_t = \tau _t$
and
$\widehat{z}_t = \tau _t$
and
![]() $\,\widehat{x}_t = \gamma \tau _t + \tau _{x,t}$
of the restricted model with
$\,\widehat{x}_t = \gamma \tau _t + \tau _{x,t}$
of the restricted model with
![]() $\varphi _\mu = \varphi _{\mu _x} =0$
. The shaded region represents the 5-th and 95-th percentiles.
$\varphi _\mu = \varphi _{\mu _x} =0$
. The shaded region represents the 5-th and 95-th percentiles.
5.3. Testing
 $\varphi _{\mu _x} = \sigma _{\eta _x}^2=0$
$\varphi _{\mu _x} = \sigma _{\eta _x}^2=0$
Now, we test the joint hypothesis that
![]() $\varphi _{\mu _x} = \sigma _{\eta _x}^2=0$
. This restriction goes to the heart of the debate between Schmitt-Grohé and Uribè (Reference Schmitt-Grohé and Uribè2011) and Benati (Reference Benati2013). If the restricted model held true, then RPI and TFP would be co-integrated as argued by Schmitt-Grohé and Uribè (Reference Schmitt-Grohé and Uribè2011). On the other hand, if the restrictions were rejected, we would end with a situation where RPI and TFP are not co-integrated, but still share a common component as shown in Benati (Reference Benati2013).
$\varphi _{\mu _x} = \sigma _{\eta _x}^2=0$
. This restriction goes to the heart of the debate between Schmitt-Grohé and Uribè (Reference Schmitt-Grohé and Uribè2011) and Benati (Reference Benati2013). If the restricted model held true, then RPI and TFP would be co-integrated as argued by Schmitt-Grohé and Uribè (Reference Schmitt-Grohé and Uribè2011). On the other hand, if the restrictions were rejected, we would end with a situation where RPI and TFP are not co-integrated, but still share a common component as shown in Benati (Reference Benati2013).
Since zero is at the boundary of the parameter space of
![]() $\sigma _{\eta _x}^2$
, the relevant Bayes factor cannot be computed using the Savage–Dickey density ratio.Footnote
5
Instead, we compute the log marginal likelihoods of the baseline model and the restricted version with
$\sigma _{\eta _x}^2$
, the relevant Bayes factor cannot be computed using the Savage–Dickey density ratio.Footnote
5
Instead, we compute the log marginal likelihoods of the baseline model and the restricted version with
![]() $\varphi _{\mu _x} = \sigma _{\eta _x}^2=0$
. The marginal likelihoods of the two models are obtained by using the adaptive importance sampling estimator known as the cross-entropy method proposed in Chan and Eisenstat (Reference Chan and Eisenstat2015).
$\varphi _{\mu _x} = \sigma _{\eta _x}^2=0$
. The marginal likelihoods of the two models are obtained by using the adaptive importance sampling estimator known as the cross-entropy method proposed in Chan and Eisenstat (Reference Chan and Eisenstat2015).
The log marginal likelihood of the baseline model is 1684, compared to 1627 of the restricted version. This means that the log Bayes factor in favor of the baseline model is 57, suggesting overwhelming support for the unrestricted model. This shows that we can reject the joint hypothesis
![]() $\varphi _{\mu _x} = \sigma _{\eta _x}^2=0$
. This result along with the fact that
$\varphi _{\mu _x} = \sigma _{\eta _x}^2=0$
. This result along with the fact that
![]() $\gamma \gt 0$
implies a positive covariation between RPI and TFP. While this conclusion is identical to the result in Benati (Reference Benati2013), our approach sets itself apart in the sense that it provides a quantitative measure of the relationship between the trends in RPI and TFP, and it offers an interpretation that may be easily traced to economic theory. Furthermore, it strengthens the argument suggested by many studies that DSGE models should be modified to incorporate the joint long-run relationship between NT and IST as misspecification may lead to misleading conclusions about sources of business cycle fluctuations. For instance, while both Schmitt-Grohé and Uribè (Reference Schmitt-Grohé and Uribè2011) and Benati (Reference Benati2013) adopt different strategies, the results in both studies appear to indicate (1) the presence of a common relationship between NT and IST (the authors differ in their views about the nature of this common relationship), and (2) the emergence of a new, common stochastic trend shocks, that play a more significant role than each technology shocks in the business cycle fluctuations of macro variables. Schmitt-Grohé and Uribè (Reference Schmitt-Grohé and Uribè2011) manage to incorporate this common relationship, in the form of a co-integration assumption, in a DSGE model to gauge the role of the new shocks, but Benati (Reference Benati2013) uses the co-variation result in a VAR setting. Since our framework delivers results which seems to align with those in Benati (Reference Benati2013), we argue that our structural framework may help to guide the joint co-variation specification in DSGE models, in the spirit of Ferroni (Reference Ferroni2011) and Canova (Reference Canova2014).
$\gamma \gt 0$
implies a positive covariation between RPI and TFP. While this conclusion is identical to the result in Benati (Reference Benati2013), our approach sets itself apart in the sense that it provides a quantitative measure of the relationship between the trends in RPI and TFP, and it offers an interpretation that may be easily traced to economic theory. Furthermore, it strengthens the argument suggested by many studies that DSGE models should be modified to incorporate the joint long-run relationship between NT and IST as misspecification may lead to misleading conclusions about sources of business cycle fluctuations. For instance, while both Schmitt-Grohé and Uribè (Reference Schmitt-Grohé and Uribè2011) and Benati (Reference Benati2013) adopt different strategies, the results in both studies appear to indicate (1) the presence of a common relationship between NT and IST (the authors differ in their views about the nature of this common relationship), and (2) the emergence of a new, common stochastic trend shocks, that play a more significant role than each technology shocks in the business cycle fluctuations of macro variables. Schmitt-Grohé and Uribè (Reference Schmitt-Grohé and Uribè2011) manage to incorporate this common relationship, in the form of a co-integration assumption, in a DSGE model to gauge the role of the new shocks, but Benati (Reference Benati2013) uses the co-variation result in a VAR setting. Since our framework delivers results which seems to align with those in Benati (Reference Benati2013), we argue that our structural framework may help to guide the joint co-variation specification in DSGE models, in the spirit of Ferroni (Reference Ferroni2011) and Canova (Reference Canova2014).
5.4. Testing
 $\varphi _\mu = \varphi _{\mu _x} = 1$
$\varphi _\mu = \varphi _{\mu _x} = 1$
Lastly, we test the joint hypothesis that
![]() $\varphi _\mu = \varphi _{\mu _x} = 1$
. This restriction would imply that the trend components in RPI and TFP follow an ARIMA(0,2,0) process such that the growth rate of these trends is integrated of order one.
$\varphi _\mu = \varphi _{\mu _x} = 1$
. This restriction would imply that the trend components in RPI and TFP follow an ARIMA(0,2,0) process such that the growth rate of these trends is integrated of order one.
Since the value 1 is at the boundary of the parameter space of both
![]() $\varphi _\mu$
and
$\varphi _\mu$
and
![]() $\varphi _{\mu _x}$
, the relevant Bayes factor cannot be computed using the Savage–Dickey density ratio. We instead compute the log marginal likelihoods of the baseline model and the restricted version with
$\varphi _{\mu _x}$
, the relevant Bayes factor cannot be computed using the Savage–Dickey density ratio. We instead compute the log marginal likelihoods of the baseline model and the restricted version with
![]() $\varphi _\mu = \varphi _{\mu _x} = 1$
, again using the cross-entropy method in Chan and Eisenstat (Reference Chan and Eisenstat2015). The former value is 1684 and the latter is 1034, suggesting overwhelming support for the baseline model. Hence, we can reject the joint hypothesis
$\varphi _\mu = \varphi _{\mu _x} = 1$
, again using the cross-entropy method in Chan and Eisenstat (Reference Chan and Eisenstat2015). The former value is 1684 and the latter is 1034, suggesting overwhelming support for the baseline model. Hence, we can reject the joint hypothesis
![]() $\varphi _\mu = \varphi _{\mu _x} = 1$
. These are consistent with the estimation results reported in Table 1. Specifically, under the baseline model,
$\varphi _\mu = \varphi _{\mu _x} = 1$
. These are consistent with the estimation results reported in Table 1. Specifically, under the baseline model,
![]() $\varphi _\mu$
and
$\varphi _\mu$
and
![]() $\varphi _{\mu _x}$
are estimated to be, respectively, 0.101 and
$\varphi _{\mu _x}$
are estimated to be, respectively, 0.101 and
![]() $-0.051$
, and both values are far from 1. These results are quite reassuring because if the restricted model held true, then we may be tempted to impose an ARMA(0,2,0) specification for NT and IST. However, this would be hard to reconcile with the fact that output growth has been documented in many studies to follow a positively autocorrelated AR(1) process. Since output dynamics are essentially determined by impulse dynamics, an ARMA(0,2,0) process for technology would indicate that output growth is integrated of order one, violating that stylized fact.
$-0.051$
, and both values are far from 1. These results are quite reassuring because if the restricted model held true, then we may be tempted to impose an ARMA(0,2,0) specification for NT and IST. However, this would be hard to reconcile with the fact that output growth has been documented in many studies to follow a positively autocorrelated AR(1) process. Since output dynamics are essentially determined by impulse dynamics, an ARMA(0,2,0) process for technology would indicate that output growth is integrated of order one, violating that stylized fact.
6. Conclusion
The aim of the paper is to evaluate the relationship between the RPI and TFP to inform the specification of NT and IST in DSGE models. Using the UC decomposition that allows us to separate a trend component from a cyclical component in a time series, we specify a model that features a common component between the trends component in RPI and TFP. The main results of the analysis is that RPI and TFP may each be generated by an ARIMA(1,1,0) process, and the two series share a common stochastic trend component that may drive the mean growth rate of aggregate productivity in the USA. As documented in many studies, we view this common stochastic trend component as capturing permanent changes in GPT from innovations in information and communication technologies. In addition, our findings provide some guidance to the idiosyncratic and joint specification of NT and IST in DSGE models. This may help to reduce misspecification errors that contribute to misleading interpretations about the sources of business cycles and the analysis of output dynamics.
A. Appendix
A.1. Model Economy
In this section, we use a neoclassical model similar to the structure in Greenwood et al. (Reference Greenwood, Hercowitz and Huffman1997a, Reference Greenwood, Hercowitz and Per1997b), Oulton (Reference Oulton2007), and Moura (Reference Moura2021) to derive our UC framework in equations (1)–(6). Consider the following model:
Equation (A.1) is the aggregate production function where output, (
![]() $Y_{t}$
), which can be used for either consumption, (
$Y_{t}$
), which can be used for either consumption, (
![]() $C_{t}$
), or gross investment, (
$C_{t}$
), or gross investment, (
![]() $I_{t}$
), is produced with capital, (
$I_{t}$
), is produced with capital, (
![]() $K_{t}$
), and labor, (
$K_{t}$
), and labor, (
![]() $h_{t}$
) such that
$h_{t}$
) such that
![]() $0 \leq h_{t} \leq 1$
. The production function is subjected to a stationary neutral technological shock, (
$0 \leq h_{t} \leq 1$
. The production function is subjected to a stationary neutral technological shock, (
![]() $a_{t}$
), and a nonstationary neutral technological shock, (
$a_{t}$
), and a nonstationary neutral technological shock, (
![]() $X_{t}^{z}$
). Equation (A.2) relates investment in efficiency units, (
$X_{t}^{z}$
). Equation (A.2) relates investment in efficiency units, (
![]() $I_{t}^{*}$
), to gross investment. The terms
$I_{t}^{*}$
), to gross investment. The terms
![]() $a_{t}$
and
$a_{t}$
and
![]() $X_{t}^{a}$
denote, respectively, stationary and nonstationary IST. Finally, equation (A.3) shows the evolution of the capital stock. It is important to note that output and gross investment are both measured in units of consumption goods.
$X_{t}^{a}$
denote, respectively, stationary and nonstationary IST. Finally, equation (A.3) shows the evolution of the capital stock. It is important to note that output and gross investment are both measured in units of consumption goods.
In this model economy, TFP and the RPI, denoted as
![]() $P_{t}^{I}$
, are given, respectively, by:
$P_{t}^{I}$
, are given, respectively, by:
Along a balanced growth path, the stochastic trend in
![]() $Y_{t}$
and
$Y_{t}$
and
![]() $C_{t}$
is given by
$C_{t}$
is given by
![]() $X_{t}^{z}\left (X_{t}^{a}\right )^{\frac{\alpha }{1-\alpha }}$
, while the stochastic trend in investment measured in efficiency units
$X_{t}^{z}\left (X_{t}^{a}\right )^{\frac{\alpha }{1-\alpha }}$
, while the stochastic trend in investment measured in efficiency units
![]() $I_{t}^{*}$
is
$I_{t}^{*}$
is
![]() $X_{t}^{z}\left (X_{t}^{a}\right )^{\frac{1}{1-\alpha }}$
.
$X_{t}^{z}\left (X_{t}^{a}\right )^{\frac{1}{1-\alpha }}$
.
Using the standard Divisia definition of aggregate output, output,
![]() $Y_{t}^{D}$
, is well approximated by a share weighted index:Footnote 6
$Y_{t}^{D}$
, is well approximated by a share weighted index:Footnote 6
where
![]() $\gamma$
is the current price share of investment in the value of output. Under this definition of output, TFP is defined as:
$\gamma$
is the current price share of investment in the value of output. Under this definition of output, TFP is defined as:
Therefore, expressions (A.4) and (A.7) may be combined to yield
To determine the stochastic balanced growth path in
![]() $\text{TFP}_{t}^{D}$
, we start with expression (A.8) and apply the logarithm on both sides:
$\text{TFP}_{t}^{D}$
, we start with expression (A.8) and apply the logarithm on both sides:
then we take the first difference, and use the definition in (A.6) to get
 \begin{align*} \log (\text{TFP}_{t}^{D})-\log (\text{TFP}_{t-1}^{D}) &= (1-\alpha )\left (\log X_{t}^{z} -\log X_{t-1}^{z} \right ) + (1-\gamma )\left (\log C_{t} -\log C_{t-1} \right )\\[5pt] &\quad + \gamma \left (\log I_{t}^{*} -\log I_{t-1}^{*} \right ) - \left (\log Y_{t} -\log Y_{t-1} \right )\\[5pt] &= (1-\alpha )\left (\log X_{t}^{z} -\log X_{t-1}^{z} \right )\\[5pt] &\quad + (1-\gamma )\left [\log \left (X_{t}^{z}\left (X_{t}^{a}\right )^{\frac{\alpha }{1-\alpha }}\right )-\log \left (X_{t-1}^{z}\left (X_{t-1}^{a}\right )^{\frac{\alpha }{1-\alpha }}\right )\right ]\\[5pt] &\quad + \gamma \left [ \log \left (X_{t}^{z}\left (X_{t}^{a}\right )^{\frac{1}{1-\alpha }}\right )-\log \left (X_{t-1}^{z}\left (X_{t-1}^{a}\right )^{\frac{1}{1-\alpha }}\right )\right ]\\[5pt] & \quad - \left [\log \left (X_{t}^{z}\left (X_{t}^{a}\right )^{\frac{\alpha }{1-\alpha }}\right ) -\log \left (X_{t-1}^{z}\left (X_{t-1}^{a}\right )^{\frac{\alpha }{1-\alpha }}\right )\right ] \\[5pt] &= (1-\alpha )\left (\log X_{t}^{z} -\log X_{t-1}^{z} \right ) + \gamma \left [\log X_{t}^{a}-\log X_{t-1}^{a}\right ] \end{align*}
\begin{align*} \log (\text{TFP}_{t}^{D})-\log (\text{TFP}_{t-1}^{D}) &= (1-\alpha )\left (\log X_{t}^{z} -\log X_{t-1}^{z} \right ) + (1-\gamma )\left (\log C_{t} -\log C_{t-1} \right )\\[5pt] &\quad + \gamma \left (\log I_{t}^{*} -\log I_{t-1}^{*} \right ) - \left (\log Y_{t} -\log Y_{t-1} \right )\\[5pt] &= (1-\alpha )\left (\log X_{t}^{z} -\log X_{t-1}^{z} \right )\\[5pt] &\quad + (1-\gamma )\left [\log \left (X_{t}^{z}\left (X_{t}^{a}\right )^{\frac{\alpha }{1-\alpha }}\right )-\log \left (X_{t-1}^{z}\left (X_{t-1}^{a}\right )^{\frac{\alpha }{1-\alpha }}\right )\right ]\\[5pt] &\quad + \gamma \left [ \log \left (X_{t}^{z}\left (X_{t}^{a}\right )^{\frac{1}{1-\alpha }}\right )-\log \left (X_{t-1}^{z}\left (X_{t-1}^{a}\right )^{\frac{1}{1-\alpha }}\right )\right ]\\[5pt] & \quad - \left [\log \left (X_{t}^{z}\left (X_{t}^{a}\right )^{\frac{\alpha }{1-\alpha }}\right ) -\log \left (X_{t-1}^{z}\left (X_{t-1}^{a}\right )^{\frac{\alpha }{1-\alpha }}\right )\right ] \\[5pt] &= (1-\alpha )\left (\log X_{t}^{z} -\log X_{t-1}^{z} \right ) + \gamma \left [\log X_{t}^{a}-\log X_{t-1}^{a}\right ] \end{align*}
where we use the fact that, along a balanced growth path,
![]() $Y_{t}$
and
$Y_{t}$
and
![]() $C_{t}$
grow at the same rate as
$C_{t}$
grow at the same rate as
![]() $X_{t}^{z}\left (X_{t}^{a}\right )^{\frac{\alpha }{1-\alpha }}$
, while
$X_{t}^{z}\left (X_{t}^{a}\right )^{\frac{\alpha }{1-\alpha }}$
, while
![]() $I_{t}^{*}$
grows at the faster rate
$I_{t}^{*}$
grows at the faster rate
![]() $X_{t}^{z}\left (X_{t}^{a}\right )^{\frac{1}{1-\alpha }}$
. Then, using a simple change of variable to specify technology so that it is Hicks neutral instead of Harrod neutral, that is,
$X_{t}^{z}\left (X_{t}^{a}\right )^{\frac{1}{1-\alpha }}$
. Then, using a simple change of variable to specify technology so that it is Hicks neutral instead of Harrod neutral, that is,
![]() $\widetilde{X}_{t}^{z} = \left (X_{t}^{z}\right )^{1-\alpha }$
, we obtain
$\widetilde{X}_{t}^{z} = \left (X_{t}^{z}\right )^{1-\alpha }$
, we obtain
or in other words, along the balanced growth path,
![]() $\frac{\text{TFP}_{t}^{D}}{\widetilde{X}_{t}^{z}\left ( X_{t}^{a}\right )^{\gamma }}$
is stationary. We may apply the same logic to the relative price of investment,
$\frac{\text{TFP}_{t}^{D}}{\widetilde{X}_{t}^{z}\left ( X_{t}^{a}\right )^{\gamma }}$
is stationary. We may apply the same logic to the relative price of investment,
![]() $P_{t}^{I}$
, to show that
$P_{t}^{I}$
, to show that
![]() $P_{t}^{I}X_{t}^{a}$
is also stationary along the stochastic balanced growth path. Let
$P_{t}^{I}X_{t}^{a}$
is also stationary along the stochastic balanced growth path. Let
![]() $\text{tfp}_{t}^{D}$
and
$\text{tfp}_{t}^{D}$
and
![]() $p_{t}^{I}$
denote stationary TFP and stationary RPI, respectively; therefore, applying the logarithm and rearranging yields the system:
$p_{t}^{I}$
denote stationary TFP and stationary RPI, respectively; therefore, applying the logarithm and rearranging yields the system:
Suppose that we further assume that the growth rate of the nonstationary NT, and the nonstationary IST, denoted as
![]() $\mu _{t}^{z} \equiv \Delta \log \widetilde{X}_{t}^{z}$
and
$\mu _{t}^{z} \equiv \Delta \log \widetilde{X}_{t}^{z}$
and
![]() $\mu _{t}^{a} \equiv \Delta \log X_{t}^{a}$
, respectively, follow stationary
$\mu _{t}^{a} \equiv \Delta \log X_{t}^{a}$
, respectively, follow stationary
![]() $\text{AR}(1)$
processes, and the stationary components of TFP and RPI,
$\text{AR}(1)$
processes, and the stationary components of TFP and RPI,
![]() $\log \text{tfp}_{t}^{D}$
and
$\log \text{tfp}_{t}^{D}$
and
![]() $\log p_{t}^{I}$
, follow
$\log p_{t}^{I}$
, follow
![]() $\text{AR}(1)$
processes as we specify in the paper. Therefore, equations (A.12) and (A.13) along with the assumed specifications constitute the full characterization of our UC framework illustrated in equations (1)–(6) within the manuscript.
$\text{AR}(1)$
processes as we specify in the paper. Therefore, equations (A.12) and (A.13) along with the assumed specifications constitute the full characterization of our UC framework illustrated in equations (1)–(6) within the manuscript.
We may also use our framework to derive expressions for RPI and TFP in terms of NT and IST shocks to obtain sensible restrictions for the identification of these shocks in a VAR framework. We will assume without loss of generality that both NT and IST follow a unit root process such that
![]() $\widetilde{X}_{t}^{z} = \widetilde{X}_{t-1}^{z}\exp (\varepsilon ^{z}_{t})$
and
$\widetilde{X}_{t}^{z} = \widetilde{X}_{t-1}^{z}\exp (\varepsilon ^{z}_{t})$
and
![]() $X_{t}^{a} = X_{t-1}^{a}\exp (\varepsilon ^{a}_{t})$
. In that case,
$X_{t}^{a} = X_{t-1}^{a}\exp (\varepsilon ^{a}_{t})$
. In that case,
![]() $\varepsilon _{t}^{z}$
and
$\varepsilon _{t}^{z}$
and
![]() $\varepsilon _{t}^{a}$
are the NT shocks and the IST shocks, respectively.
$\varepsilon _{t}^{a}$
are the NT shocks and the IST shocks, respectively.
For RPI, we apply the log to expression (A.5) and take the first difference to get
 \begin{align*} \begin{split} \log P_{t}^{I} - \log P_{t-1}^{I} &= - \log X_{t}^{a} + \log X_{t-1}^{a} - \log a_{t} + \log a_{t-1}\\ \log P_{t}^{I} - \log P_{t-1}^{I} &= - \log X_{t}^{a} + \log X_{t-1}^{a}\\ \Delta \log P_{t}^{I} &= - \varepsilon _{t}^{a} \end{split} \end{align*}
\begin{align*} \begin{split} \log P_{t}^{I} - \log P_{t-1}^{I} &= - \log X_{t}^{a} + \log X_{t-1}^{a} - \log a_{t} + \log a_{t-1}\\ \log P_{t}^{I} - \log P_{t-1}^{I} &= - \log X_{t}^{a} + \log X_{t-1}^{a}\\ \Delta \log P_{t}^{I} &= - \varepsilon _{t}^{a} \end{split} \end{align*}
Note that since
![]() $a_{t}$
follows stationary process, its growth rate,
$a_{t}$
follows stationary process, its growth rate,
![]() $\log a_{t} - \log a_{t-1}$
, may be assumed to be approximately equal to zero.
$\log a_{t} - \log a_{t-1}$
, may be assumed to be approximately equal to zero.
We apply the same logic to TFP in the case when output is expressed in consumption units. Specifically, applying the log to expression (A.4) and taking the first difference yields
 \begin{align*} \begin{split} \log \text{TFP}_{t} - \log \text{TFP}_{t-1} &= \log \widetilde{X}_{t}^{z} - \log \widetilde{X}_{t-1}^{z} + \log z_{t} - \log z_{t-1}\\ \log \text{TFP}_{t} - \log \text{TFP}_{t-1} &= \log \widetilde{X}_{t}^{z} - \log \widetilde{X}_{t-1}^{z}\\ \Delta \log \text{TFP}_{t} &= \varepsilon _{t}^{z} \end{split} \end{align*}
\begin{align*} \begin{split} \log \text{TFP}_{t} - \log \text{TFP}_{t-1} &= \log \widetilde{X}_{t}^{z} - \log \widetilde{X}_{t-1}^{z} + \log z_{t} - \log z_{t-1}\\ \log \text{TFP}_{t} - \log \text{TFP}_{t-1} &= \log \widetilde{X}_{t}^{z} - \log \widetilde{X}_{t-1}^{z}\\ \Delta \log \text{TFP}_{t} &= \varepsilon _{t}^{z} \end{split} \end{align*}
where we assume again that the growth rate of
![]() $z_{t}$
is approximately equal to zero. Note that technology is Hicks neutral, that is,
$z_{t}$
is approximately equal to zero. Note that technology is Hicks neutral, that is,
![]() $\widetilde{X}_{t}^{z} = \left (X_{t}^{z}\right )^{1-\alpha }$
.
$\widetilde{X}_{t}^{z} = \left (X_{t}^{z}\right )^{1-\alpha }$
.
In the case when output is measured via the Divisia index, we rely on expression (A.9) to obtain
In sum, the expressions for RPI and TFP in terms of the NT and IST shocks are given by:
From expression (A.14), it is evident that a positive IST shock (
![]() $\varepsilon _{t}^{a} \gt 0$
) has a permanent impact on the log level of the relative price of investment. When output is measured in consumption units, expression (A.15) shows that only NT affects the log level of TFP permanently. With Divisia index output, both NT and IST affect TFP. Therefore, the definition of output matters for the identification of NT shocks and IST in a bivariate system consisting of the log difference of RPI and the log difference of TFP.
$\varepsilon _{t}^{a} \gt 0$
) has a permanent impact on the log level of the relative price of investment. When output is measured in consumption units, expression (A.15) shows that only NT affects the log level of TFP permanently. With Divisia index output, both NT and IST affect TFP. Therefore, the definition of output matters for the identification of NT shocks and IST in a bivariate system consisting of the log difference of RPI and the log difference of TFP.
A.2. Common Trend in RPI and TFP
In this section, we empirically revisit two issues that have been explored in both Schmitt-Grohé and Uribè (Reference Schmitt-Grohé and Uribè2011) and Benati (Reference Benati2013). The first is to determine whether RPI and TFP possess each a stochastic nonstationary component, and the second is to assess whether these nonstationary components are related. Therefore, we perform unit root tests and co-integration tests using US data over the period
![]() $1959:Q2$
to
$1959:Q2$
to
![]() $2019.Q2$
using the logarithm of RPI and the logarithm of TFP.
$2019.Q2$
using the logarithm of RPI and the logarithm of TFP.
A.3. Unit Root Tests
We carry out Augmented–Dickey Fuller (ADF) tests that examine the null hypothesis that the logarithms of RPI and TFP have a unit root. The lag order is chosen based on the Schwartz information criterion (SIC) and Hannah–Quinn (HQ) criterion.Footnote 7 The results of the tests are presented in Table 2, and they clearly indicate that the tests fail to reject the null hypothesis of the presence of a unit root in the series at the standard 5% confidence level.
Table 2. ADF test: testing the null hypothesis of the presence of a unit root

Note: ADF stands for Augmented Dickey–Fuller test. RPI and TFP stand for relative price of investment and total factor productivity, respectively. In all cases, the model includes a constant and a time trend. The data series span from
![]() $1959.II$
to
$1959.II$
to
![]() $2019.II.$
The lag order is selected according to the SIC and HQ criterion.
$2019.II.$
The lag order is selected according to the SIC and HQ criterion.
An alternative to the ADF test is the Kwiatkowski, Phillips, Schmidt, and Shin (KPSS) test that evaluates the null hypothesis that the time series is stationary in levels. The lag length is still selected according to the SIC and HQ criterion, and we allow for the possibility of a time trend in the series. The results are illustrated in Table 3, and they are consistent with those obtained from ADF tests: the KPSS rejects the null hypothesis of stationarity in the logarithm of the relative price of investment and total factor productivity.
Table 3. KPSS test: testing the null hypothesis of stationarity

Note: RPI and TFP stand for relative price of investment and total factor productivity, respectively. In all cases, the model includes a constant and time trend. The data series span from
![]() $1959.II$
to
$1959.II$
to
![]() $2019.II$
. The lag order is selected according to the SIC and HQ criterion.
$2019.II$
. The lag order is selected according to the SIC and HQ criterion.
Overall, stationarity tests are unequivocal in terms of the univariate properties of RPI and TFP: both time series contain a stochastic nonstationary component.
A.4. Co-integration between RPI and TFP
The results from the previous section clearly indicate that the time series of both RPI and TFP contain a nonstationary stochastic component. With that information at hand, we assess the extent to which these two non-stochastic components might be co-integrated. Specifically, we perform the Johansen’s trace test that evaluates the null hypothesis that there is no co-integration relationship between the two series. A rejection of this hypothesis would indicate that RPI and TFP are driven by a single stochastic component. Consistent with the previous section, we still select the lag length according to the SIC and HQ criterion, and the result points to 1 as the optimal lag order. As discussed in Benati (Reference Benati2013), the lag order selection for VARs containing integrated variables in the Johansen’s procedure may greatly affect the results of the test. Therefore, we also consider lag orders of 7 and 3 as alternatives, as in Schmitt-Grohé and Uribè (Reference Schmitt-Grohé and Uribè2011) and Benati (Reference Benati2013), respectively. A final and crucial component of the test is the specification of the data generating process (DGP) for the co-integrated model as this step has great importance on the results of the test. In other words, should a deterministic term, constant or linear term, be included in the DGP? Such decisions are usually guided by the underlying process of the variables which may or may not contain a drift term. Both the inverse of RPI and TFP appear to be trending upward; hence, we consider the addition of a constant and linear term in the DGP. The results of the Johansen’s trace tests are shown in Table 4.
Table 4. Johansen’s trace test for co-integration between RPI and TFP

Note: The co-integration tests are performed on the logarithms of the relative price of investment and total factor productivity. The sample period is
![]() $1959.II$
to
$1959.II$
to
![]() $2019.II$
. The variable
$2019.II$
. The variable
![]() $r$
denotes the number of co-integrating vectors. RPI and TFP stand for relative price of investment and total factor productivity, respectively, and the model includes a constant and time trend. The lag order is selected according to the SIC and HQ criterion.
$r$
denotes the number of co-integrating vectors. RPI and TFP stand for relative price of investment and total factor productivity, respectively, and the model includes a constant and time trend. The lag order is selected according to the SIC and HQ criterion.
The co-integration results are inconclusive. When the lag order is 7, the null hypothesis of a zero co-integrating vector is rejected at the standard 5% confidence level, a result that echoes those in Benati (Reference Benati2013) and Schmitt-Grohé and Uribè (Reference Schmitt-Grohé and Uribè2011). However, the test fails to reject the null hypothesis of a zero co-integrating vector when a lag order of 1 or 3 is considered. Therefore, it appears that it is impossible to claim with certainty that RPI and TFP are driven by a single stochastic trend component.
A.5. Estimation Details
In this appendix, we provide the estimation details of the bivariate unobserved components model specified in the main text. For convenience, we reproduce the UC model below:
where
![]() $\tau _t$
and
$\tau _t$
and
![]() $\tau _{x,t}$
are the trend components, whereas
$\tau _{x,t}$
are the trend components, whereas
![]() $c_{z,t}$
and
$c_{z,t}$
and
![]() $c_{x,t}$
are the transitory components. The transitory components are assumed to follow the AR(2) processes below:
$c_{x,t}$
are the transitory components. The transitory components are assumed to follow the AR(2) processes below:
where
![]() $\epsilon _{z,t}\sim \mathcal{N}(0,\sigma _{z}^2)$
and
$\epsilon _{z,t}\sim \mathcal{N}(0,\sigma _{z}^2)$
and
![]() $\epsilon _{x,t}\sim \mathcal{N}(0,\sigma _{x}^2)$
, and the initial conditions
$\epsilon _{x,t}\sim \mathcal{N}(0,\sigma _{x}^2)$
, and the initial conditions
![]() $c_{z,0},c_{x,0},c_{z,-1}$
and
$c_{z,0},c_{x,0},c_{z,-1}$
and
![]() $c_{x,-1}$
are assumed to be zero. For the trend components, we model the first differences of
$c_{x,-1}$
are assumed to be zero. For the trend components, we model the first differences of
![]() $\Delta \tau _t$
and
$\Delta \tau _t$
and
![]() $\Delta \tau _{x,t}$
as stationary processes, each with a break at
$\Delta \tau _{x,t}$
as stationary processes, each with a break at
![]() $t = T_B$
with a different unconditional mean. More specifically, consider
$t = T_B$
with a different unconditional mean. More specifically, consider
where
![]() $1(\!\cdot\!)$
denotes the indicator function,
$1(\!\cdot\!)$
denotes the indicator function,
![]() $\eta _t\sim \mathcal{N}(0,\sigma _{\eta }^2)$
and
$\eta _t\sim \mathcal{N}(0,\sigma _{\eta }^2)$
and
![]() $\eta _{x,t}\sim \mathcal{N}(0,\sigma _{\eta _x}^2)$
are independent of each other at all leads and lags. The initial conditions
$\eta _{x,t}\sim \mathcal{N}(0,\sigma _{\eta _x}^2)$
are independent of each other at all leads and lags. The initial conditions
![]() $\boldsymbol \tau _0 = (\tau _0,\tau _{-1},\tau _{x,0},\tau _{x,-1})^{\prime }$
are treated as unknown parameters.
$\boldsymbol \tau _0 = (\tau _0,\tau _{-1},\tau _{x,0},\tau _{x,-1})^{\prime }$
are treated as unknown parameters.
Section 3 in the main text outlines a five-block posterior simulator to estimate the above bivariate unobserved components model. Below, we describe the implementation details of all the steps.
Step 1. Since
![]() $\boldsymbol \tau$
and
$\boldsymbol \tau$
and
![]() $\gamma$
enter the likelihood multiplicatively, we sample them jointly to improve the efficiency of the posterior sampler. In particular, we first sample
$\gamma$
enter the likelihood multiplicatively, we sample them jointly to improve the efficiency of the posterior sampler. In particular, we first sample
![]() $\gamma$
marginally of
$\gamma$
marginally of
![]() $\boldsymbol \tau$
, followed by drawing
$\boldsymbol \tau$
, followed by drawing
![]() $\boldsymbol \tau$
conditional on the sampled
$\boldsymbol \tau$
conditional on the sampled
![]() $\gamma$
. The latter step is straightforward as the model specified in (1)–(6) defines a linear state space model for
$\gamma$
. The latter step is straightforward as the model specified in (1)–(6) defines a linear state space model for
![]() $\boldsymbol \tau$
. In what follows, we derive the full conditional distribution of
$\boldsymbol \tau$
. In what follows, we derive the full conditional distribution of
![]() $p(\boldsymbol \tau \,|\, \textbf{y}, \gamma, \boldsymbol \phi, \boldsymbol \varphi, \boldsymbol \zeta, \boldsymbol \sigma ^2,\boldsymbol \tau _0)$
. Then, we outline a Metropolis–Hastings algorithm to sample
$p(\boldsymbol \tau \,|\, \textbf{y}, \gamma, \boldsymbol \phi, \boldsymbol \varphi, \boldsymbol \zeta, \boldsymbol \sigma ^2,\boldsymbol \tau _0)$
. Then, we outline a Metropolis–Hastings algorithm to sample
![]() $\gamma$
marginally of
$\gamma$
marginally of
![]() $\boldsymbol \tau$
.
$\boldsymbol \tau$
.
To derive the conditional distribution
![]() $p(\boldsymbol \tau \,|\, \textbf{y}, \gamma, \boldsymbol \phi, \boldsymbol \varphi, \boldsymbol \zeta, \boldsymbol \sigma ^2,\boldsymbol \tau _0)$
, note that by Bayes’ theorem we have
$p(\boldsymbol \tau \,|\, \textbf{y}, \gamma, \boldsymbol \phi, \boldsymbol \varphi, \boldsymbol \zeta, \boldsymbol \sigma ^2,\boldsymbol \tau _0)$
, note that by Bayes’ theorem we have
where the conditional likelihood
![]() $p(\textbf{y} \,|\, \boldsymbol \tau, \gamma, \boldsymbol \phi, \boldsymbol \sigma ^2)$
and the prior
$p(\textbf{y} \,|\, \boldsymbol \tau, \gamma, \boldsymbol \phi, \boldsymbol \sigma ^2)$
and the prior
![]() $p(\boldsymbol \tau \,|\, \boldsymbol \varphi, \boldsymbol \zeta, \boldsymbol \sigma ^2,\boldsymbol \tau _0)$
are, respectively, defined by the observation equations (1), (2), (5), and (6) and the state equations (3)–(4).
$p(\boldsymbol \tau \,|\, \boldsymbol \varphi, \boldsymbol \zeta, \boldsymbol \sigma ^2,\boldsymbol \tau _0)$
are, respectively, defined by the observation equations (1), (2), (5), and (6) and the state equations (3)–(4).
First, we derive the conditional likelihood
![]() $p(\textbf{y} \,|\, \boldsymbol \tau, \gamma, \boldsymbol \phi, \boldsymbol \sigma ^2)$
. Letting
$p(\textbf{y} \,|\, \boldsymbol \tau, \gamma, \boldsymbol \phi, \boldsymbol \sigma ^2)$
. Letting
![]() $\textbf{c} = (c_{z,1},c_{x,1},\ldots, c_{z,T},c_{x,T})$
’ we can stack the observation equations (1)–(2) over
$\textbf{c} = (c_{z,1},c_{x,1},\ldots, c_{z,T},c_{x,T})$
’ we can stack the observation equations (1)–(2) over
![]() $t=1,\ldots, T$
to get
$t=1,\ldots, T$
to get
where
 $\boldsymbol \Pi _{\gamma } = \textbf{I}_T\otimes \begin{pmatrix} 1 & 0 \\ \gamma & 1 \end{pmatrix}$
. Here
$\boldsymbol \Pi _{\gamma } = \textbf{I}_T\otimes \begin{pmatrix} 1 & 0 \\ \gamma & 1 \end{pmatrix}$
. Here
![]() $ \textbf{I}_T$
is the
$ \textbf{I}_T$
is the
![]() $T$
-dimensional identity matrix and
$T$
-dimensional identity matrix and
![]() $\otimes$
is the Kronecker product. Next, we stack (5)–(6) over
$\otimes$
is the Kronecker product. Next, we stack (5)–(6) over
![]() $t=1,\ldots, T$
to get
$t=1,\ldots, T$
to get
where
![]() $\boldsymbol \epsilon = (\epsilon _{z,1},\epsilon _{x,1},\ldots, \epsilon _{z,T},\epsilon _{x,T})^{\prime }$
and
$\boldsymbol \epsilon = (\epsilon _{z,1},\epsilon _{x,1},\ldots, \epsilon _{z,T},\epsilon _{x,T})^{\prime }$
and
 \begin{equation*} \textbf {H}_{\boldsymbol \phi } = \begin {pmatrix} \textbf {I}_2 & \textbf {0} & \textbf {0} & \textbf {0} & \cdots & \textbf {0} \\ \textbf {A}_{1}& \textbf {I}_2 & \textbf {0} & \textbf {0} & \cdots & \textbf {0} \\ \textbf {A}_{2}& \textbf {A}_{1}& \textbf {I}_2 & \textbf {0} & \cdots & \textbf {0} \\ \textbf {0} & \textbf {A}_{2}& \textbf {A}_{1}& \textbf {I}_2 & \cdots & \textbf {0} \\ \vdots & & \ddots & \ddots & \ddots &\vdots \\ \textbf {0} & \cdots & \textbf {0} & \textbf {A}_{2}& \textbf {A}_{1} & \textbf {I}_2 \\ \end {pmatrix} \end{equation*}
\begin{equation*} \textbf {H}_{\boldsymbol \phi } = \begin {pmatrix} \textbf {I}_2 & \textbf {0} & \textbf {0} & \textbf {0} & \cdots & \textbf {0} \\ \textbf {A}_{1}& \textbf {I}_2 & \textbf {0} & \textbf {0} & \cdots & \textbf {0} \\ \textbf {A}_{2}& \textbf {A}_{1}& \textbf {I}_2 & \textbf {0} & \cdots & \textbf {0} \\ \textbf {0} & \textbf {A}_{2}& \textbf {A}_{1}& \textbf {I}_2 & \cdots & \textbf {0} \\ \vdots & & \ddots & \ddots & \ddots &\vdots \\ \textbf {0} & \cdots & \textbf {0} & \textbf {A}_{2}& \textbf {A}_{1} & \textbf {I}_2 \\ \end {pmatrix} \end{equation*}
with
 $\textbf{A}_{1} = \begin{pmatrix} -\phi _{z,1} & 0 \\ 0 & -\phi _{x,1} \end{pmatrix}$
and
$\textbf{A}_{1} = \begin{pmatrix} -\phi _{z,1} & 0 \\ 0 & -\phi _{x,1} \end{pmatrix}$
and
 $\textbf{A}_{2} = \begin{pmatrix} -\phi _{z,2} & 0 \\ 0 & -\phi _{x,2} \end{pmatrix}$
. Since the determinant of
$\textbf{A}_{2} = \begin{pmatrix} -\phi _{z,2} & 0 \\ 0 & -\phi _{x,2} \end{pmatrix}$
. Since the determinant of
![]() $\textbf{H}_{\boldsymbol \phi }$
is one for any
$\textbf{H}_{\boldsymbol \phi }$
is one for any
![]() $\boldsymbol \phi$
, it is invertible. It follows that
$\boldsymbol \phi$
, it is invertible. It follows that
![]() $(\textbf{c}\,|\, \boldsymbol \phi, \boldsymbol \sigma ^2) \sim \mathcal{N}(\textbf{0},(\textbf{H}_{\boldsymbol \phi }^{\prime }\boldsymbol \Sigma _{\boldsymbol \epsilon }^{-1}\textbf{H}_{\boldsymbol \phi })^{-1})$
, where
$(\textbf{c}\,|\, \boldsymbol \phi, \boldsymbol \sigma ^2) \sim \mathcal{N}(\textbf{0},(\textbf{H}_{\boldsymbol \phi }^{\prime }\boldsymbol \Sigma _{\boldsymbol \epsilon }^{-1}\textbf{H}_{\boldsymbol \phi })^{-1})$
, where
![]() $\boldsymbol \Sigma _{\boldsymbol \epsilon } = \mathrm{diag}(\sigma _{z}^2,\sigma _{x}^2,\ldots,\sigma _{z}^2,\sigma _{x}^2)$
. It then follows that
$\boldsymbol \Sigma _{\boldsymbol \epsilon } = \mathrm{diag}(\sigma _{z}^2,\sigma _{x}^2,\ldots,\sigma _{z}^2,\sigma _{x}^2)$
. It then follows that
Next, we derive the prior
![]() $p(\boldsymbol \tau \,|\, \boldsymbol \varphi, \boldsymbol \zeta, \boldsymbol \sigma ^2,\boldsymbol \tau _0)$
. To that end, construct the
$p(\boldsymbol \tau \,|\, \boldsymbol \varphi, \boldsymbol \zeta, \boldsymbol \sigma ^2,\boldsymbol \tau _0)$
. To that end, construct the
![]() $T\times 1$
vector of indicators
$T\times 1$
vector of indicators
![]() $\textbf{d}_0 = (1(1\lt T_B), 1(2\lt T_B),\ldots, 1(T\lt T_B))^{\prime }$
and similarly define
$\textbf{d}_0 = (1(1\lt T_B), 1(2\lt T_B),\ldots, 1(T\lt T_B))^{\prime }$
and similarly define
![]() $\textbf{d}_1$
. Moreover, let
$\textbf{d}_1$
. Moreover, let
 \begin{equation*} \widetilde {\boldsymbol \mu }_{\boldsymbol \tau } = \textbf {d}_0\otimes \begin {pmatrix}(1-\varphi _{\mu })\zeta _1 \\ (1-\varphi _{\mu _x})\zeta _{x,1} \end {pmatrix} + \textbf {d}_1\otimes \begin {pmatrix}(1-\varphi _{\mu })\zeta _2 \\ (1-\varphi _{\mu _x})\zeta _{x,2} \end {pmatrix} + \begin {pmatrix} (1+\varphi _{\mu })\tau _0 -\varphi _{\mu }\tau _{-1} \\ (1+\varphi _{\mu _x})\tau _{x,0} -\varphi _{\mu _x}\tau _{x,-1} \\ -\varphi _{\mu }\tau _{0} \\ -\varphi _{\mu _x}\tau _{x,0} \\ 0 \\ \vdots \\ 0 \end {pmatrix}. \end{equation*}
\begin{equation*} \widetilde {\boldsymbol \mu }_{\boldsymbol \tau } = \textbf {d}_0\otimes \begin {pmatrix}(1-\varphi _{\mu })\zeta _1 \\ (1-\varphi _{\mu _x})\zeta _{x,1} \end {pmatrix} + \textbf {d}_1\otimes \begin {pmatrix}(1-\varphi _{\mu })\zeta _2 \\ (1-\varphi _{\mu _x})\zeta _{x,2} \end {pmatrix} + \begin {pmatrix} (1+\varphi _{\mu })\tau _0 -\varphi _{\mu }\tau _{-1} \\ (1+\varphi _{\mu _x})\tau _{x,0} -\varphi _{\mu _x}\tau _{x,-1} \\ -\varphi _{\mu }\tau _{0} \\ -\varphi _{\mu _x}\tau _{x,0} \\ 0 \\ \vdots \\ 0 \end {pmatrix}. \end{equation*}
Then, we can stack the state equations (A.21)–(A.22) over
![]() $t=1,\ldots, T$
to get
$t=1,\ldots, T$
to get
where
![]() $\boldsymbol \eta = (\eta _1,\eta _{x,1},\ldots, \eta _T,\eta _{x,T})^{\prime }$
and
$\boldsymbol \eta = (\eta _1,\eta _{x,1},\ldots, \eta _T,\eta _{x,T})^{\prime }$
and
 \begin{equation*} \textbf {H}_{\boldsymbol \varphi } = \begin {pmatrix} \textbf {I}_2 & \textbf {0} & \textbf {0} & \textbf {0} & \cdots & \textbf {0} \\ \textbf {B}_{1}& \textbf {I}_2 & \textbf {0} & \textbf {0} & \cdots & \textbf {0} \\ \textbf {B}_{2}& \textbf {B}_{1}& \textbf {I}_2 & \textbf {0} & \cdots & \textbf {0} \\ \textbf {0} & \textbf {B}_{2}& \textbf {B}_{1}& \textbf {I}_2 & \cdots & \textbf {0} \\ \vdots & & \ddots & \ddots & \ddots &\vdots \\ \textbf {0} & \cdots & \textbf {0} & \textbf {B}_{2}& \textbf {B}_{1} & \textbf {I}_2 \\ \end {pmatrix} \end{equation*}
\begin{equation*} \textbf {H}_{\boldsymbol \varphi } = \begin {pmatrix} \textbf {I}_2 & \textbf {0} & \textbf {0} & \textbf {0} & \cdots & \textbf {0} \\ \textbf {B}_{1}& \textbf {I}_2 & \textbf {0} & \textbf {0} & \cdots & \textbf {0} \\ \textbf {B}_{2}& \textbf {B}_{1}& \textbf {I}_2 & \textbf {0} & \cdots & \textbf {0} \\ \textbf {0} & \textbf {B}_{2}& \textbf {B}_{1}& \textbf {I}_2 & \cdots & \textbf {0} \\ \vdots & & \ddots & \ddots & \ddots &\vdots \\ \textbf {0} & \cdots & \textbf {0} & \textbf {B}_{2}& \textbf {B}_{1} & \textbf {I}_2 \\ \end {pmatrix} \end{equation*}
with
 $\textbf{B}_{1} = \begin{pmatrix} -(1+\varphi _{\mu }) & 0 \\ 0 & -(1+\varphi _{\mu _x}) \end{pmatrix}$
and
$\textbf{B}_{1} = \begin{pmatrix} -(1+\varphi _{\mu }) & 0 \\ 0 & -(1+\varphi _{\mu _x}) \end{pmatrix}$
and
 $\textbf{B}_{2} = \begin{pmatrix} \varphi _{\mu } & 0 \\ 0 & \varphi _{\mu _x} \end{pmatrix}$
. Since the determinant of
$\textbf{B}_{2} = \begin{pmatrix} \varphi _{\mu } & 0 \\ 0 & \varphi _{\mu _x} \end{pmatrix}$
. Since the determinant of
![]() $\textbf{H}_{\boldsymbol \varphi }$
is one for any
$\textbf{H}_{\boldsymbol \varphi }$
is one for any
![]() $\boldsymbol \varphi$
, it is invertible. It then follows that
$\boldsymbol \varphi$
, it is invertible. It then follows that
where
![]() $\boldsymbol \mu _{\boldsymbol \tau } = \textbf{H}_{\boldsymbol \varphi }^{-1}\widetilde{\boldsymbol \mu }_{\boldsymbol \tau }$
and
$\boldsymbol \mu _{\boldsymbol \tau } = \textbf{H}_{\boldsymbol \varphi }^{-1}\widetilde{\boldsymbol \mu }_{\boldsymbol \tau }$
and
![]() $\boldsymbol \Sigma _{\eta } = \mathrm{diag}(\sigma _{\eta }^2,\sigma _{\eta _x}^2,\ldots,\sigma _{\eta }^2,\sigma _{\eta _x}^2)$
. Combining (A.23) and (A.24) and using standard regression results (see, e.g., Chan et al. (Reference Chan, Koop, Poirier and Tobias2019), pp. 217–219), we have
$\boldsymbol \Sigma _{\eta } = \mathrm{diag}(\sigma _{\eta }^2,\sigma _{\eta _x}^2,\ldots,\sigma _{\eta }^2,\sigma _{\eta _x}^2)$
. Combining (A.23) and (A.24) and using standard regression results (see, e.g., Chan et al. (Reference Chan, Koop, Poirier and Tobias2019), pp. 217–219), we have
where
Since the precision matrix
![]() $\textbf{K}_{\boldsymbol \tau }$
is banded—that is, it is sparse and its nonzero elements are arranged along the main diagonal—one can sample from
$\textbf{K}_{\boldsymbol \tau }$
is banded—that is, it is sparse and its nonzero elements are arranged along the main diagonal—one can sample from
![]() $p(\boldsymbol \tau \,|\, \textbf{y}, \gamma, \boldsymbol \phi, \boldsymbol \varphi, \boldsymbol \zeta, \boldsymbol \sigma ^2,\boldsymbol \tau _0)$
efficiently using the precision sampler in Chan and Jeliazkov (Reference Chan and Jeliazkov2009).
$p(\boldsymbol \tau \,|\, \textbf{y}, \gamma, \boldsymbol \phi, \boldsymbol \varphi, \boldsymbol \zeta, \boldsymbol \sigma ^2,\boldsymbol \tau _0)$
efficiently using the precision sampler in Chan and Jeliazkov (Reference Chan and Jeliazkov2009).
Next, we outline a Metropolis–Hastings algorithm to sample
![]() $\gamma$
marginally of
$\gamma$
marginally of
![]() $\boldsymbol \tau$
. For that, we need to evaluate the integrated likelihood:
$\boldsymbol \tau$
. For that, we need to evaluate the integrated likelihood:
Traditionally, this is done by using the Kalman filter. However, it turns out that we can obtain an analytical expression of the integrated likelihood and evaluate it efficiently using band matrix routines. Using a similar derivation in Chan and Grant (Reference Chan and Grant2016), one can show that
 \begin{equation} \begin{split} p(\textbf{y} & \,|\, \gamma, \boldsymbol \phi, \boldsymbol \varphi, \boldsymbol \zeta, \boldsymbol \sigma ^2,\boldsymbol \tau _0) \\ & = (2\pi )^{-T} |\boldsymbol \Sigma _{\boldsymbol \epsilon }|^{-\frac{1}{2}} |\boldsymbol \Sigma _{\boldsymbol \eta }|^{-\frac{1}{2}}|\textbf{K}_{\boldsymbol \tau }|^{-\frac{1}{2}} \mathrm{e}^{-\frac{1}{2}\left (\textbf{y}^{\prime }\textbf{H}_{\boldsymbol \phi }^{\prime }\boldsymbol \Sigma _{\boldsymbol \epsilon }^{-1}\textbf{H}_{\boldsymbol \phi }\textbf{y} + \boldsymbol \mu _{\boldsymbol \tau }^{\prime }\textbf{H}_{\boldsymbol \varphi }^{\prime }\boldsymbol \Sigma _{\boldsymbol \eta }^{-1}\textbf{H}_{\boldsymbol \varphi }\boldsymbol \mu _{\boldsymbol \tau } - \widehat{\boldsymbol \tau }^{\prime }\textbf{K}_{\boldsymbol \tau }\widehat{\boldsymbol \tau }\right )}. \end{split} \end{equation}
\begin{equation} \begin{split} p(\textbf{y} & \,|\, \gamma, \boldsymbol \phi, \boldsymbol \varphi, \boldsymbol \zeta, \boldsymbol \sigma ^2,\boldsymbol \tau _0) \\ & = (2\pi )^{-T} |\boldsymbol \Sigma _{\boldsymbol \epsilon }|^{-\frac{1}{2}} |\boldsymbol \Sigma _{\boldsymbol \eta }|^{-\frac{1}{2}}|\textbf{K}_{\boldsymbol \tau }|^{-\frac{1}{2}} \mathrm{e}^{-\frac{1}{2}\left (\textbf{y}^{\prime }\textbf{H}_{\boldsymbol \phi }^{\prime }\boldsymbol \Sigma _{\boldsymbol \epsilon }^{-1}\textbf{H}_{\boldsymbol \phi }\textbf{y} + \boldsymbol \mu _{\boldsymbol \tau }^{\prime }\textbf{H}_{\boldsymbol \varphi }^{\prime }\boldsymbol \Sigma _{\boldsymbol \eta }^{-1}\textbf{H}_{\boldsymbol \varphi }\boldsymbol \mu _{\boldsymbol \tau } - \widehat{\boldsymbol \tau }^{\prime }\textbf{K}_{\boldsymbol \tau }\widehat{\boldsymbol \tau }\right )}. \end{split} \end{equation}
The above expression involves a few large matrices, but they are all banded. Consequently, it can be evaluated efficiently using band matrix algorithms; see Chan and Grant (Reference Chan and Grant2016) for technical details.
Finally, we implement a Metropolis–Hastings step to sample
![]() $\gamma$
with the Gaussian proposal
$\gamma$
with the Gaussian proposal
![]() $\mathcal{N}(\widehat{\gamma },K_{\gamma }^{-1})$
, where
$\mathcal{N}(\widehat{\gamma },K_{\gamma }^{-1})$
, where
![]() $\widehat{\gamma }$
is the mode of
$\widehat{\gamma }$
is the mode of
![]() $\log p(\textbf{y} \,|\, \gamma, \boldsymbol \phi, \boldsymbol \varphi, \boldsymbol \zeta, \boldsymbol \sigma ^2,\boldsymbol \tau _0)$
and
$\log p(\textbf{y} \,|\, \gamma, \boldsymbol \phi, \boldsymbol \varphi, \boldsymbol \zeta, \boldsymbol \sigma ^2,\boldsymbol \tau _0)$
and
![]() $K_{\gamma }$
is the negative Hessian evaluated at the mode.
$K_{\gamma }$
is the negative Hessian evaluated at the mode.
Step 2. To sample
![]() $\boldsymbol \phi$
, we write (A.19)–(A.20) as a regression with coefficient vector
$\boldsymbol \phi$
, we write (A.19)–(A.20) as a regression with coefficient vector
![]() $\boldsymbol \phi$
:
$\boldsymbol \phi$
:
where
![]() $\textbf{c} = (c_{z,1}, c_{x,1}, \ldots, c_{z,T}, c_{x,T})^{\prime }$
and
$\textbf{c} = (c_{z,1}, c_{x,1}, \ldots, c_{z,T}, c_{x,T})^{\prime }$
and
![]() $\textbf{X}_{\boldsymbol \phi }$
is a
$\textbf{X}_{\boldsymbol \phi }$
is a
![]() $2T\times 4$
matrix consisting of lagged values of
$2T\times 4$
matrix consisting of lagged values of
![]() $(c_{z,t}, c_{x,t})$
. Then, by standard regression results, we have
$(c_{z,t}, c_{x,t})$
. Then, by standard regression results, we have
where
A draw from this truncated normal distribution can be obtained by the acceptance–rejection method, that is, keep sampling from
![]() $\mathcal{N}(\widehat{\boldsymbol \phi },\textbf{K}_{\boldsymbol \phi }^{-1})$
until
$\mathcal{N}(\widehat{\boldsymbol \phi },\textbf{K}_{\boldsymbol \phi }^{-1})$
until
![]() $\boldsymbol \phi \in \textbf{R}$
.
$\boldsymbol \phi \in \textbf{R}$
.
Step 3. Next, we simulate from
![]() $p(\boldsymbol \varphi \,|\, \textbf{y}, \boldsymbol \tau, \gamma, \boldsymbol \phi, \boldsymbol \zeta, \boldsymbol \sigma ^2,\boldsymbol \tau _0)$
. As in Step 2, we first write (A.21)–(A.22) as a regression with coefficient vector
$p(\boldsymbol \varphi \,|\, \textbf{y}, \boldsymbol \tau, \gamma, \boldsymbol \phi, \boldsymbol \zeta, \boldsymbol \sigma ^2,\boldsymbol \tau _0)$
. As in Step 2, we first write (A.21)–(A.22) as a regression with coefficient vector
![]() $\boldsymbol \varphi$
:
$\boldsymbol \varphi$
:
where
![]() $\Delta \boldsymbol \tau = (\Delta \tau _1,\Delta \tau _{x,1},\ldots, \Delta \tau _T,\Delta \tau _{x,T})^{\prime }, \boldsymbol \mu _{\boldsymbol \varphi } = (\zeta _1 1(1\lt T_B) + \zeta _2 1(1\geq T_B),\ldots, \zeta _1 1(T\lt T_B) + \zeta _2 1(T\geq T_B))^{\prime }$
and
$\Delta \boldsymbol \tau = (\Delta \tau _1,\Delta \tau _{x,1},\ldots, \Delta \tau _T,\Delta \tau _{x,T})^{\prime }, \boldsymbol \mu _{\boldsymbol \varphi } = (\zeta _1 1(1\lt T_B) + \zeta _2 1(1\geq T_B),\ldots, \zeta _1 1(T\lt T_B) + \zeta _2 1(T\geq T_B))^{\prime }$
and
 \begin{equation*} \textbf {X}_{\boldsymbol \varphi } = \begin {pmatrix} \Delta \tau _{0} - \zeta _1 1(1\lt T_B) - \zeta _2 1(1\geq T_B) & 0 \\ 0 & \Delta \tau _{x,0} - \zeta _{x,1} 1(1\lt T_B) - \zeta _{x,2} 1(1\geq T_B) \\ \vdots & \vdots \\ \Delta \tau _{T-1} - \zeta _1 1(T\lt T_B) - \zeta _2 1(T\geq T_B) & 0 \\ 0 & \Delta \tau _{x,T-1} - \zeta _{x,1} 1(T\lt T_B) - \zeta _{x,2} 1(T\geq T_B) \end {pmatrix}. \end{equation*}
\begin{equation*} \textbf {X}_{\boldsymbol \varphi } = \begin {pmatrix} \Delta \tau _{0} - \zeta _1 1(1\lt T_B) - \zeta _2 1(1\geq T_B) & 0 \\ 0 & \Delta \tau _{x,0} - \zeta _{x,1} 1(1\lt T_B) - \zeta _{x,2} 1(1\geq T_B) \\ \vdots & \vdots \\ \Delta \tau _{T-1} - \zeta _1 1(T\lt T_B) - \zeta _2 1(T\geq T_B) & 0 \\ 0 & \Delta \tau _{x,T-1} - \zeta _{x,1} 1(T\lt T_B) - \zeta _{x,2} 1(T\geq T_B) \end {pmatrix}. \end{equation*}
Again, by standard regression results, we have
where
A draw from this truncated normal distribution can be obtained by the acceptance–rejection method.
Step 4. To implement Step 4, note that
![]() $\sigma _{\eta }^2, \sigma _{\eta _x}^2, \sigma _{z}^2, \sigma _{x}^2$
are conditionally independent given
$\sigma _{\eta }^2, \sigma _{\eta _x}^2, \sigma _{z}^2, \sigma _{x}^2$
are conditionally independent given
![]() $\boldsymbol \tau$
and other parameters. Moreover, since the priors on
$\boldsymbol \tau$
and other parameters. Moreover, since the priors on
![]() $\sigma _{z}^2$
and
$\sigma _{z}^2$
and
![]() $\sigma _{x}^2$
are inverse-gamma, so are the full posterior conditional distributions:
$\sigma _{x}^2$
are inverse-gamma, so are the full posterior conditional distributions:
 \begin{align*} (\sigma ^2_{z} \,|\, \textbf{y}, \boldsymbol \tau, \gamma, \boldsymbol \phi, \boldsymbol \varphi, \boldsymbol \zeta,\boldsymbol \tau _0) & \sim \mathcal{IG}\left (\nu _z+\frac{T}{2}, S_{z} + \frac{1}{2}\sum _{t=1}^T\epsilon _{z,t}^2\right ), \end{align*}
\begin{align*} (\sigma ^2_{z} \,|\, \textbf{y}, \boldsymbol \tau, \gamma, \boldsymbol \phi, \boldsymbol \varphi, \boldsymbol \zeta,\boldsymbol \tau _0) & \sim \mathcal{IG}\left (\nu _z+\frac{T}{2}, S_{z} + \frac{1}{2}\sum _{t=1}^T\epsilon _{z,t}^2\right ), \end{align*}
 \begin{align*} (\sigma ^2_{x} \,|\, \textbf{y}, \boldsymbol \tau, \gamma, \boldsymbol \phi, \boldsymbol \varphi, \boldsymbol \zeta,\boldsymbol \tau _0) & \sim \mathcal{IG}\left (\nu _x+\frac{T}{2}, S_{x} + \frac{1}{2}\sum _{t=1}^T\epsilon _{x,t}^2\right ). \end{align*}
\begin{align*} (\sigma ^2_{x} \,|\, \textbf{y}, \boldsymbol \tau, \gamma, \boldsymbol \phi, \boldsymbol \varphi, \boldsymbol \zeta,\boldsymbol \tau _0) & \sim \mathcal{IG}\left (\nu _x+\frac{T}{2}, S_{x} + \frac{1}{2}\sum _{t=1}^T\epsilon _{x,t}^2\right ). \end{align*}
For
![]() $\sigma _{\eta }^2$
and
$\sigma _{\eta }^2$
and
![]() $ \sigma _{\eta _x}^2$
, recall that they have gamma priors:
$ \sigma _{\eta _x}^2$
, recall that they have gamma priors:
![]() $\sigma _{\eta }^2 \sim \mathcal{G}(1/2,1/(2V_{\sigma _{\eta }}))$
and
$\sigma _{\eta }^2 \sim \mathcal{G}(1/2,1/(2V_{\sigma _{\eta }}))$
and
![]() $\sigma _{\eta _x}^2 \sim \mathcal{G}(1/2,1/(2V_{\sigma _{\eta _x}}))$
. Hence, the full conditional density of
$\sigma _{\eta _x}^2 \sim \mathcal{G}(1/2,1/(2V_{\sigma _{\eta _x}}))$
. Hence, the full conditional density of
![]() $\sigma ^2_{\eta }$
is given by:
$\sigma ^2_{\eta }$
is given by:
which is not a standard distribution. However, we can sample
![]() $\sigma ^2_{\eta }$
via a Metropolis–Hastings step. Specifically, we first obtain a candidate draw
$\sigma ^2_{\eta }$
via a Metropolis–Hastings step. Specifically, we first obtain a candidate draw
![]() $\sigma ^{2*}_{\eta }$
from the proposal distribution
$\sigma ^{2*}_{\eta }$
from the proposal distribution
![]() $\sigma ^{2*}_{\eta }\sim \mathcal{IG}((T-1)/2, \sum _{t=1}^T\eta _t^2/2).$
Then, given the current draw
$\sigma ^{2*}_{\eta }\sim \mathcal{IG}((T-1)/2, \sum _{t=1}^T\eta _t^2/2).$
Then, given the current draw
![]() $\sigma ^{2}_{\eta }$
, we accept the candidate with probability:
$\sigma ^{2}_{\eta }$
, we accept the candidate with probability:
 \begin{equation*} \min \left \{1, \frac {\mathrm {e}^{\frac {1}{2 V_{\sigma _\eta }}\sigma _{\eta }^{2*}}} {\mathrm {e}^{\frac {1}{2 V_{\sigma _\eta }}\sigma _{\eta }^{2}}}\right \}. \end{equation*}
\begin{equation*} \min \left \{1, \frac {\mathrm {e}^{\frac {1}{2 V_{\sigma _\eta }}\sigma _{\eta }^{2*}}} {\mathrm {e}^{\frac {1}{2 V_{\sigma _\eta }}\sigma _{\eta }^{2}}}\right \}. \end{equation*}
Similarly, we can sample
![]() $\sigma ^2_{\eta _x}$
by first obtaining a candidate
$\sigma ^2_{\eta _x}$
by first obtaining a candidate
![]() $\sigma ^{2*}_{\eta _x}\sim \mathcal{IG}((T-1)/2, \sum _{t=1}^T\eta _{x,t}^2/2).$
Then, given the current
$\sigma ^{2*}_{\eta _x}\sim \mathcal{IG}((T-1)/2, \sum _{t=1}^T\eta _{x,t}^2/2).$
Then, given the current
![]() $\sigma ^{2}_{\eta _x}$
, we accept the candidate with probability
$\sigma ^{2}_{\eta _x}$
, we accept the candidate with probability
 \begin{equation*} \min \left \{1, \frac {\mathrm {e}^{\frac {1}{2 V_{\sigma _{\eta _x}}}\sigma _{\eta _x}^{2*}}} {\mathrm {e}^{\frac {1}{2 V_{\sigma _{\eta _x}}}\sigma _{\eta _x}^{2}}}\right \}. \end{equation*}
\begin{equation*} \min \left \{1, \frac {\mathrm {e}^{\frac {1}{2 V_{\sigma _{\eta _x}}}\sigma _{\eta _x}^{2*}}} {\mathrm {e}^{\frac {1}{2 V_{\sigma _{\eta _x}}}\sigma _{\eta _x}^{2}}}\right \}. \end{equation*}
Step 5. Next, we jointly sample
![]() $\boldsymbol \delta = (\boldsymbol \zeta ^{\prime },\boldsymbol \tau _0^{\prime })^{\prime }$
from its full conditional distribution. To that end, we write (A.21)–(A.22) as a regression with coefficient vector
$\boldsymbol \delta = (\boldsymbol \zeta ^{\prime },\boldsymbol \tau _0^{\prime })^{\prime }$
from its full conditional distribution. To that end, we write (A.21)–(A.22) as a regression with coefficient vector
![]() $\boldsymbol \delta$
:
$\boldsymbol \delta$
:
where
 \begin{equation*} \textbf {X}_{\boldsymbol \delta } = \left (\begin {array}{cc} \textbf {d}_0\otimes \begin {pmatrix} 1-\varphi _\mu & 0 \\ 0 & 1-\varphi _{\mu _x} \end {pmatrix} & \textbf {d}_1\otimes \begin {pmatrix} 1-\varphi _\mu & 0 \\ 0 & 1-\varphi _{\mu _x} \end {pmatrix} \end {array}\begin {array}{cccc} 1+\varphi _{\mu } & -\varphi _{\mu } & 0 & 0 \\ 0 & 0 & 1+\varphi _{\mu _x} & -\varphi _{\mu _x} \\ -\varphi _{\mu } & 0 & 0 & 0 \\ 0 & 0 & -\varphi _{\mu _x} & 0 \\ 0 & 0 & 0 & 0 \\ \vdots & \vdots & \vdots & \vdots \\ 0 & 0 & 0 & 0 \\ \end {array}\right ). \end{equation*}
\begin{equation*} \textbf {X}_{\boldsymbol \delta } = \left (\begin {array}{cc} \textbf {d}_0\otimes \begin {pmatrix} 1-\varphi _\mu & 0 \\ 0 & 1-\varphi _{\mu _x} \end {pmatrix} & \textbf {d}_1\otimes \begin {pmatrix} 1-\varphi _\mu & 0 \\ 0 & 1-\varphi _{\mu _x} \end {pmatrix} \end {array}\begin {array}{cccc} 1+\varphi _{\mu } & -\varphi _{\mu } & 0 & 0 \\ 0 & 0 & 1+\varphi _{\mu _x} & -\varphi _{\mu _x} \\ -\varphi _{\mu } & 0 & 0 & 0 \\ 0 & 0 & -\varphi _{\mu _x} & 0 \\ 0 & 0 & 0 & 0 \\ \vdots & \vdots & \vdots & \vdots \\ 0 & 0 & 0 & 0 \\ \end {array}\right ). \end{equation*}
Then, by standard regression results, we have
where
where
![]() $\textbf{V}_{\boldsymbol \delta } = \mathrm{diag}(\textbf{V}_{\boldsymbol \zeta },\textbf{V}_{\boldsymbol \tau 0})$
and
$\textbf{V}_{\boldsymbol \delta } = \mathrm{diag}(\textbf{V}_{\boldsymbol \zeta },\textbf{V}_{\boldsymbol \tau 0})$
and
![]() $\boldsymbol \delta _0 = (\boldsymbol \zeta _0^{\prime },\boldsymbol \tau _{00}^{\prime })^{\prime }$
.
$\boldsymbol \delta _0 = (\boldsymbol \zeta _0^{\prime },\boldsymbol \tau _{00}^{\prime })^{\prime }$
.
A.6. A Monte Carlo Study
The section provides Monte Carlo results to assess the empirical performance of two Bayesian procedures to test the null hypothesis that
![]() $\gamma =0$
. The first approach constructs a 95% credible interval for
$\gamma =0$
. The first approach constructs a 95% credible interval for
![]() $\gamma$
, and the null hypothesis is rejected if the credible interval excludes 0. The second approach computes the Bayes factor against the null hypothesis via the Savage–Dickey density ratio
$\gamma$
, and the null hypothesis is rejected if the credible interval excludes 0. The second approach computes the Bayes factor against the null hypothesis via the Savage–Dickey density ratio
![]() $p(\gamma =0)/p(\gamma =0\,|\, \textbf{y})$
. Following Kass and Raftery (Reference Kass and Raftery1995), we interpret a value of Bayes factor larger than
$p(\gamma =0)/p(\gamma =0\,|\, \textbf{y})$
. Following Kass and Raftery (Reference Kass and Raftery1995), we interpret a value of Bayes factor larger than
![]() $\sqrt{10}$
as substantial evidence against the null hypothesis; a value less than
$\sqrt{10}$
as substantial evidence against the null hypothesis; a value less than
![]() $1/\sqrt{10}$
is viewed as substantial evidence in favor of the null hypothesis; and the test is indecisive for values in between.
$1/\sqrt{10}$
is viewed as substantial evidence in favor of the null hypothesis; and the test is indecisive for values in between.
We first generate 200 datasets from the the unobserved components model in equations (1)–(6) with
![]() $\gamma = 0$
and
$\gamma = 0$
and
![]() $T=500$
. The values of other parameter are set to be the same as the estimates reported in Table 1. Given each dataset, we then estimate the model and conduct the two hypothesis tests described above. The results are reported in Table 5. For the first hypothesis test based on the credible interval, it works well and has about the right size. For the test based on the Bayes factor, it rejects the null hypothesis
$T=500$
. The values of other parameter are set to be the same as the estimates reported in Table 1. Given each dataset, we then estimate the model and conduct the two hypothesis tests described above. The results are reported in Table 5. For the first hypothesis test based on the credible interval, it works well and has about the right size. For the test based on the Bayes factor, it rejects the null hypothesis
![]() $\gamma =0$
for about 2.5% of the datasets, whereas it rejects the alternative hypothesis
$\gamma =0$
for about 2.5% of the datasets, whereas it rejects the alternative hypothesis
![]() $\gamma \neq 0$
for about 8.5% of the datasets.Footnote 8 That is, when the null hypothesis is true, the Bayes factor favors the null hypothesis 3.4 times more frequently than the alternative
$\gamma \neq 0$
for about 8.5% of the datasets.Footnote 8 That is, when the null hypothesis is true, the Bayes factor favors the null hypothesis 3.4 times more frequently than the alternative
![]() $\gamma \neq 0$
(though it is indecisive for the majority of datasets.)
$\gamma \neq 0$
(though it is indecisive for the majority of datasets.)
Table 5. Frequencies (%) of rejecting the null hypothesis
![]() $\gamma = 0$
from the two hypothesis tests: a 95% credible interval excluding 0 and a Bayes factor value larger than
$\gamma = 0$
from the two hypothesis tests: a 95% credible interval excluding 0 and a Bayes factor value larger than
![]() $\sqrt{10}$
$\sqrt{10}$

Next, we repeat the Monte Carlo experiment, but now we set
![]() $\gamma = 1$
. In this case, the hypothesis test based on the credible interval rejects the null hypothesis for about 81% of the datasets. For the test based on the Bayes factor, it rejects the null hypothesis for about 84% of the datasets and it never rejects the alternative hypothesis
$\gamma = 1$
. In this case, the hypothesis test based on the credible interval rejects the null hypothesis for about 81% of the datasets. For the test based on the Bayes factor, it rejects the null hypothesis for about 84% of the datasets and it never rejects the alternative hypothesis
![]() $\gamma \neq 0$
. Overall, these Monte Carlo results show that both hypothesis tests work reasonably well.
$\gamma \neq 0$
. Overall, these Monte Carlo results show that both hypothesis tests work reasonably well.




















