Article contents
A symmetric 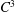 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}C^{3}$ non-stationary subdivision scheme
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}C^{3}$ non-stationary subdivision scheme
Published online by Cambridge University Press: 01 June 2014
Abstract
This paper proposes a new family of symmetric 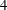 $4$ -point ternary non-stationary subdivision schemes that can generate the limit curves of
$4$ -point ternary non-stationary subdivision schemes that can generate the limit curves of 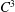 $C^3$ continuity. The continuity of this scheme is higher than the existing 4-point ternary approximating schemes. The proposed scheme has been developed using trigonometric B-spline basis functions and analyzed using the theory of asymptotic equivalence. It has the ability to reproduce or regenerate the conic sections, trigonometric polynomials and trigonometric splines as well. Some graphical and numerical examples are being considered, by choosing an appropriate tension parameter
$C^3$ continuity. The continuity of this scheme is higher than the existing 4-point ternary approximating schemes. The proposed scheme has been developed using trigonometric B-spline basis functions and analyzed using the theory of asymptotic equivalence. It has the ability to reproduce or regenerate the conic sections, trigonometric polynomials and trigonometric splines as well. Some graphical and numerical examples are being considered, by choosing an appropriate tension parameter 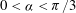 $0<\alpha <\pi /3 $ , to show the usefulness of the proposed scheme. Moreover, the Hölder regularity and the reproduction property are also being calculated.
$0<\alpha <\pi /3 $ , to show the usefulness of the proposed scheme. Moreover, the Hölder regularity and the reproduction property are also being calculated.
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- © The Author(s) 2014
References
- 2
- Cited by

