Article contents
Squarefree values of trinomial discriminants
Published online by Cambridge University Press: 01 January 2015
Abstract
The discriminant of a trinomial of the form 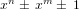 $x^{n}\pm \,x^{m}\pm \,1$ has the form
$x^{n}\pm \,x^{m}\pm \,1$ has the form 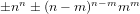 $\pm n^{n}\pm (n-m)^{n-m}m^{m}$ if
$\pm n^{n}\pm (n-m)^{n-m}m^{m}$ if  $n$ and
$n$ and 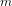 $m$ are relatively prime. We investigate when these discriminants have nontrivial square factors. We explain various unlikely-seeming parametric families of square factors of these discriminant values: for example, when
$m$ are relatively prime. We investigate when these discriminants have nontrivial square factors. We explain various unlikely-seeming parametric families of square factors of these discriminant values: for example, when  $n$ is congruent to 2 (mod 6) we have that
$n$ is congruent to 2 (mod 6) we have that 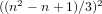 $((n^{2}-n+1)/3)^{2}$ always divides
$((n^{2}-n+1)/3)^{2}$ always divides 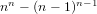 $n^{n}-(n-1)^{n-1}$ . In addition, we discover many other square factors of these discriminants that do not fit into these parametric families. The set of primes whose squares can divide these sporadic values as
$n^{n}-(n-1)^{n-1}$ . In addition, we discover many other square factors of these discriminants that do not fit into these parametric families. The set of primes whose squares can divide these sporadic values as  $n$ varies seems to be independent of
$n$ varies seems to be independent of 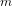 $m$ , and this set can be seen as a generalization of the Wieferich primes, those primes
$m$ , and this set can be seen as a generalization of the Wieferich primes, those primes  $p$ such that
$p$ such that 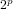 $2^{p}$ is congruent to 2 (mod
$2^{p}$ is congruent to 2 (mod 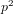 $p^{2}$ ). We provide heuristics for the density of these sporadic primes and the density of squarefree values of these trinomial discriminants.
$p^{2}$ ). We provide heuristics for the density of these sporadic primes and the density of squarefree values of these trinomial discriminants.
Information
- Type
- Research Article
- Information
- Copyright
- © The Author(s) 2015
References
- 14
- Cited by

