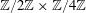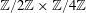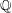Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Dujella, Andrej
and
Peral, Juan Carlos
2014.
Elliptic curves coming from Heron triangles.
Rocky Mountain Journal of Mathematics,
Vol. 44,
Issue. 4,
Dujella, Andrej
Gusić, Ivica
and
Tadić, Petra
2015.
The rank and generators of Kihara’s elliptic curve with torsion $\mathbf{Z}/4\mathbf{Z}$ over $\mathbf{Q}(t)$.
Proceedings of the Japan Academy, Series A, Mathematical Sciences,
Vol. 91,
Issue. 8,
Mikić, Miljen
2015.
On the Mordell-Weil group of elliptic curves induced by families of Diophantine triples.
Rocky Mountain Journal of Mathematics,
Vol. 45,
Issue. 5,
Dujella, Andrej
Peral, Juan Carlos
and
Tadić, Petra
2016.
Elliptic curves with torsion group Z/6Z.
Glasnik Matematicki,
Vol. 51,
Issue. 2,
p.
321.
Dujella, Andrej
Kazalicki, Matija
Mikić, Miljen
and
Szikszai, Márton
2017.
There Are Infinitely Many Rational Diophantine Sextuples.
International Mathematics Research Notices,
Vol. 2017,
Issue. 2,
p.
490.
Dujella, Andrej
Jukić Bokun, Mirela
and
Soldo, Ivan
2017.
On the torsion group of elliptic curves induced by Diophantine triples over quadratic fields.
Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A. Matemáticas,
Vol. 111,
Issue. 4,
p.
1177.
Moody, Dustin
Sadek, Mohammad
and
Zargar, Arman Shamsi
2019.
Families of elliptic curves of rank $\geq 5$ over $\mathbb Q(t)$.
Rocky Mountain Journal of Mathematics,
Vol. 49,
Issue. 7,
Dujella, Andrej
and
Peral, Juan Carlos
2019.
Elliptic curves induced by Diophantine triples.
Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A. Matemáticas,
Vol. 113,
Issue. 2,
p.
791.
Dujella, Andrej
and
Peral, Juan Carlos
2020.
High rank elliptic curves induced by rational Diophantine triples.
Glasnik Matematicki,
Vol. 55,
Issue. 2,
p.
237.
Dujella, Andrej
and
Petričević, Vinko
2020.
Diophantine quadruples with the properties $$D(n_1)$$ and $$D(n_2)$$.
Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A. Matemáticas,
Vol. 114,
Issue. 1,
YOUMBAI, Ahmed El Amine
ULUDAĞ, A. Muhammed
and
BEHLOUL, Djilali
2021.
Elliptic curve involving subfamilies of rank at least 5 over $\mathbb{Q}(t)$ or $\mathbb{Q}(t,k)$.
Hacettepe Journal of Mathematics and Statistics,
Vol. 50,
Issue. 3,
p.
721.
Dujella, Andrej
and
Peral, Juan Carlos
2021.
Construction of High Rank Elliptic Curves.
The Journal of Geometric Analysis,
Vol. 31,
Issue. 7,
p.
6698.
Mina, Renz Jimwel S.
and
Bacani, Jerico B.
2022.
Mathematics and Computing.
Vol. 415,
Issue. ,
p.
155.
Dujella, Andrej
and
Soydan, Gökhan
2022.
On elliptic curves induced by rational Diophantine quadruples.
Proceedings of the Japan Academy, Series A, Mathematical Sciences,
Vol. 98,
Issue. 1,
Dujella, Andrej
2024.
Diophantine m-tuples and Elliptic Curves.
Vol. 79,
Issue. ,
p.
87.